One end of a horizontal string is attached to a vibrating blade , and the other end passes over a pulley as in Fig. 7.49 (a). A sphere of mass 2.00kg hangs at the end of the string . The string is vibrating in its second harmonic . A container of water is raised under the sphere so that the sphere is completely submerged . In this configuration , the string vibrates in its fifth harmonic as shown in Fig . 7.49 (b). What is the radius of the sphere ?
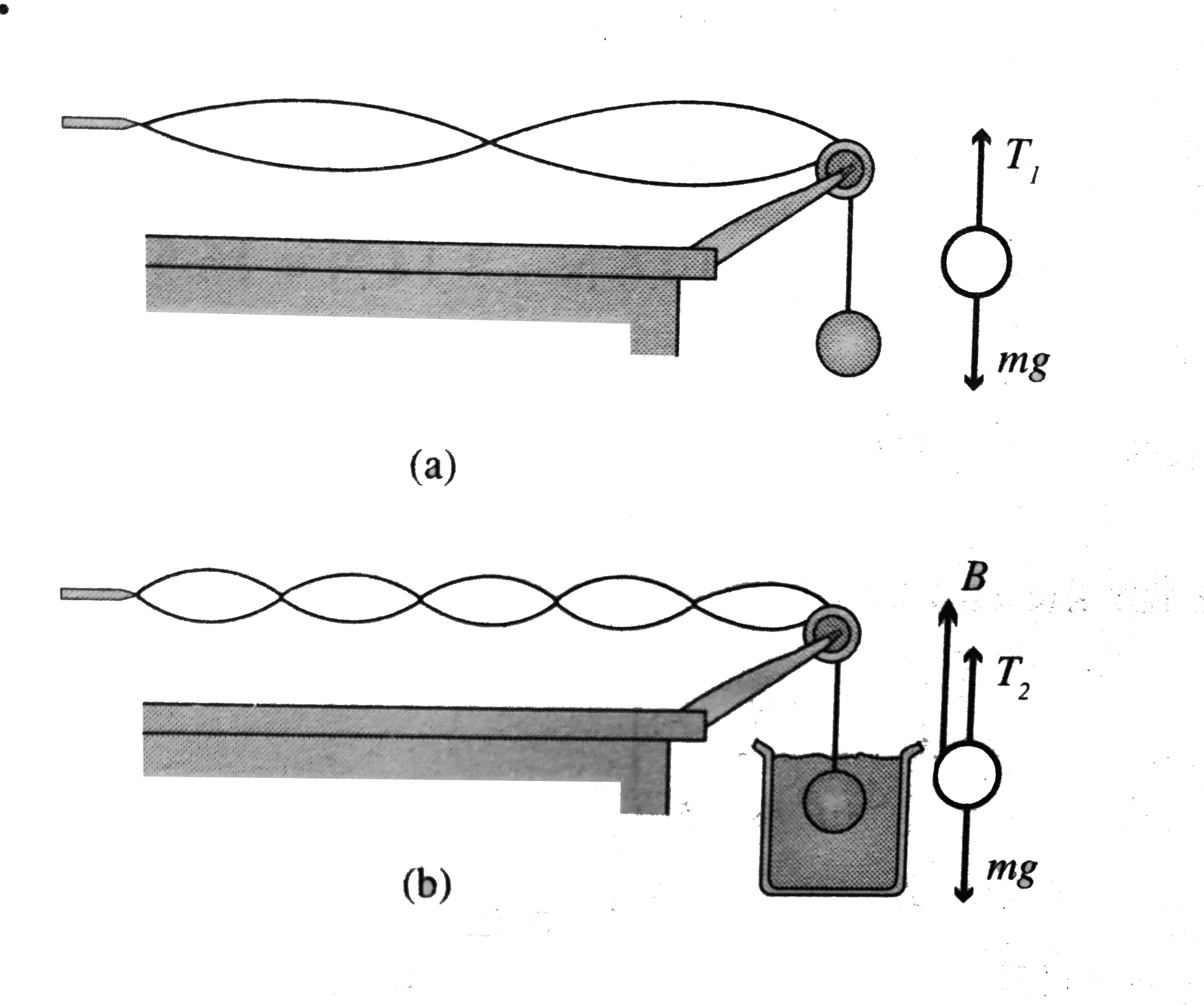
Imagine what happens when the sphere is immersed in the water . The buoyant force acts upward on the sphere , reducing the tension in the string . The change in tension causes a change in the speed of waves on the string , which in turn causes a change in the wavelength . This altered wavelength results in the string vibrating in its normal mode rather than the second .
The hanging sphere is modelled as a particle in equilibrium . One of the forces acting on it is the buoyant force from the water . we also apply the waves under boundary conditions model to the string .
Apply the particle in equilibrium model to the sphere in Fig . 7.49 (a) , identifying T1 as the tension in the string as the sphere hangs in air .
T1=mg (i)
Apply the particle in equilibrium model to the sphere in Fig . 7.49 (b) , where T2 is the tension in the string as the sphere is immersed in water . ltbr> B+T2=mg⇒B=mg−T2 (ii)
The desired quantity , the radius of the sphere , will appear in the expression for the buoyant force B . Before proceeding in this direction , however , we must evalute T2 from the information about the standing wave .
Write the equation for the frequency of a standing wave on a string twice , once before the sphere is immersed and once after . Notice that the frequency f is same in both the cases because it is determined by the vibrating blade . In addition , the linear mass density μ and the length L of the vibrating portion of the string are same in both cases . Divide the two equations.
f=n12L√T1μ (iii)
f=n22L√T2μ (iv)
1=n1n2√T1T2 (v)
solve for T2:
T2=(n1n2)2T1=(25)2(19.6N)=3.14N
Substituting this result into Eq. (ii)
B=mg−T2=19.6N−3.14N=16.5N
Now B=ρwatergVsphere=ρwaterg(43πr3)
Solve for the radius of the sphere :
r=(3B4πρwaterg)1/3
=3(16.5N)(4π(1000kg/m3)(9.80m/s2))1/3
=7.38×10−2m=7.38cm
Notice that only certain radii of the sphere will result in the string vibrating in a normal mode , the speed of waves on the string must be changed to a value such that the length of the string is integer multiple of half wavelengths . The radii of the sphere that cause the string to vibrate in a normal mode are quantized.
Similar Questions
Figure shows a string stretched by a block going over a pulley. The string vibrates in its tenth harmonic in unison with a particular tuning fork. When a beaker containing water is brought under the block so that the block is completely dipped into the beaker, the string vibrates in its eleventh harmonic. Find the density of the material of the block.
 .
.
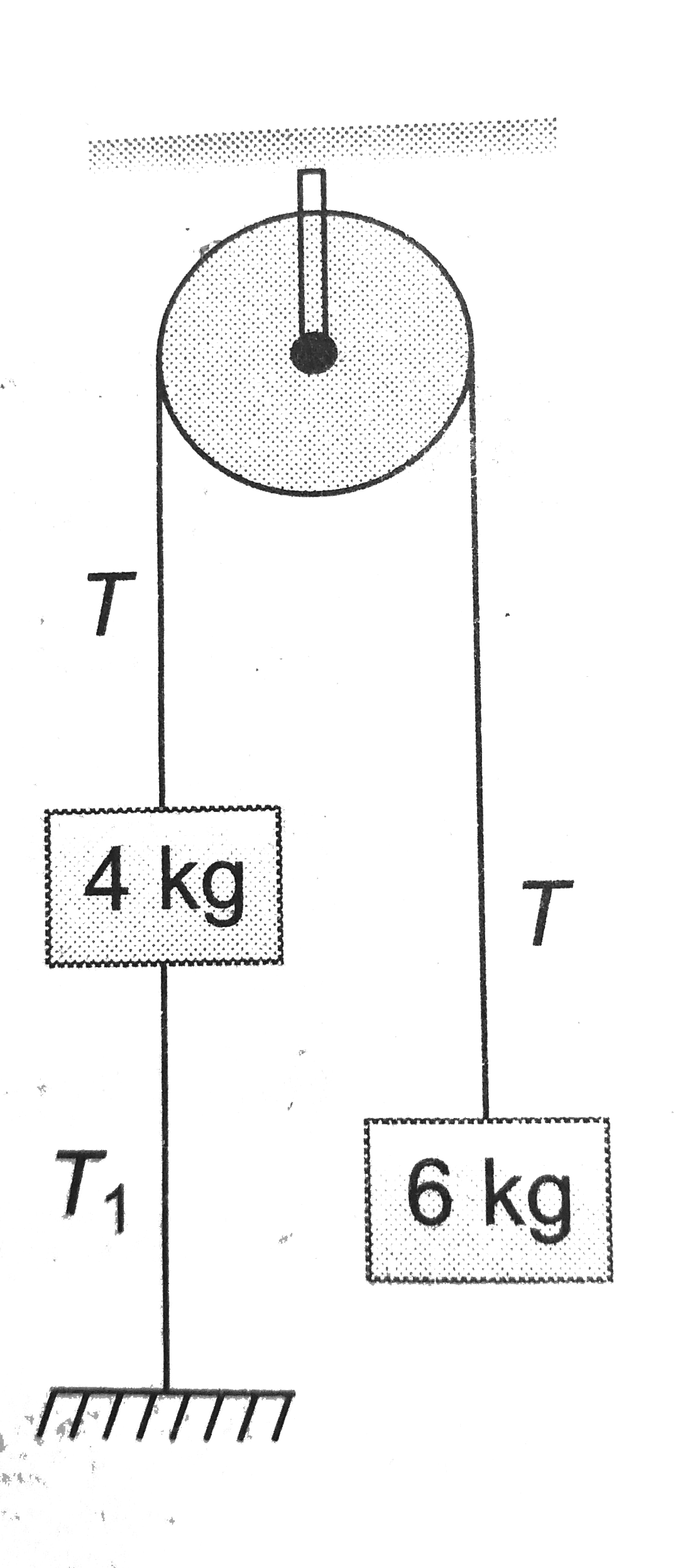
View SolutionTwo bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
View SolutionA string clamped at both ends vibrates in its fundamental mode. Is there any position (except the ends) on the string which can be touched without disturbing the motion ? What if the string vibrates in its first overtone ?
View SolutionA string is stretched by a block going over a pulley . The string vibrates in its fifth harmonic in unison with a particular tuning fork . When a beaker containing a liquid of density ρ is brought under the block so that the block is completely dipped into the beaker , the string vibrates in its seventh harmonic in unison with the tuning fork . Find the density of the material of the block.
View SolutionTwo bodies of mass 4kg and 6kg are attached to the ends of a string passing over a pulley. The 4kg mass is attached to the table top by another string. The tension in this string T1 is equal to: Take
View SolutionA string 2.0 m long and fixed at its ends is driven by a 240 Hz vibrator. The string vibrates in its third harmonic mode. The speed of the wave and its fundamental frequency is
View Solutiontwo masses 2m and m are attached to the the ends of a string while passing over a smooth Pulley of mass m and radius R. The ratio of tensions in both the strings is
_PHY_E05_245_Q01.png)
View SolutionA mass m rests on a horizontal table. It is attached to a light inextensible string which passes over a smooth pulley and carries a mass m at the other end. If the mass m is raised vertically through a distance h and is then dropped, what is the speed with which the mass 2m begins to rise?

View SolutionA string of length l is fixed at both ends and is vibrating in second harmonic. The amplitude at anti-node is 5 mm. The amplitude of a particle at distance l/8 from the fixed end is
View SolutionA hollow pipe of length 0.8m is closed at one end. At its open end a 0.5m long uniform string is vibrating in its second harmonic and it resonates with the fundamental frequency of the pipe. If the tension in the wire is 50N and the speed of sound is 320ms−1, the mass of the string is
View Solution
