Calculate the volume occupied by 2.0mol of N2 at 200K and 10.1325MPa pressure if PcVcRTc=38 and PrVrTr=2.21.
To solve the problem of calculating the volume occupied by 2.0mol of N₂ at 200K and 10.1325MPa pressure, we will follow these steps:
Step 1: Understand the relationships
We know that:
- \( P_r = \frac{P}{P_c} \)
- \( V_r = \frac{V}{V_c} \)
- \( T_r = \frac{T}{T_c} \)
Where \( P_c \), \( V_c \), and \( T_c \) are the critical pressure, volume, and temperature respectively.
Step 2: Use the given equations
From the problem, we have:
- \( \frac{P_c V_c}{R T_c} = \frac{3}{8} \) (Equation 1)
- \( \frac{P_r V_r}{T_r} = 2.21 \) (Equation 2)
Step 3: Multiply the two equations
Multiplying both equations gives:
\(
\frac{P_c V_c}{R T_c} \cdot \frac{P_r V_r}{T_r} = \frac{3}{8} \cdot 2.21
\)
Step 4: Substitute the definitions of \( P_r \), \( V_r \), and \( T_r \)
Substituting the definitions into the equation:
\(
\frac{P_c V_c}{R T_c} \cdot \frac{P}{P_c} \cdot \frac{V}{V_c} \cdot \frac{T}{T_c} = \frac{3}{8} \cdot 2.21
\)
Step 5: Simplify the equation
This simplifies to:
\(
\frac{PV}{RT} = \frac{3}{8} \cdot 2.21
\)
Step 6: Calculate the right-hand side
Calculate \( \frac{3}{8} \cdot 2.21 \):
\(
\frac{3 \cdot 2.21}{8} = 0.82875
\)
Step 7: Use the ideal gas law
Using the ideal gas law, we can express the molar volume \( V_m \):
\(
V_m = \frac{RT}{P}
\)
Equating it to the previous result:
\(
\frac{PV}{RT} = 0.82875 \implies V = 0.82875 \cdot \frac{RT}{P}
\)
Step 8: Substitute values
Using \( R = 0.0821 \, \text{L bar K}^{-1} \text{mol}^{-1} \), \( T = 200 \, K \), and converting \( P = 10.1325 \, \text{MPa} \) to bar:
\(
P = 10.1325 \times 10^6 \, \text{Pa} = \frac{10.1325 \times 10^6}{10^5} \, \text{bar} = 101.325 \, \text{bar}
\)
Step 9: Calculate the volume for one mole
Now substituting the values into the equation:
\(
V = 0.82875 \cdot \frac{0.0821 \cdot 200}{101.325}
\)
Step 10: Calculate the final volume
Calculating:
\(
V = 0.82875 \cdot \frac{16.42}{101.325} \approx 0.82875 \cdot 0.162 \approx 0.134 \, \text{L}
\)
Step 11: Calculate the volume for 2 moles
Since we have 2.0mol of N₂, the total volume is:
\(
V_{total} = 2 \cdot 0.134 \approx 0.268 \, \text{L} = 268 \, \text{mL}
\)
Final Answer
The volume occupied by 2.0mol of N₂ at 200K and 10.1325MPa is approximately 268 mL.
---
We know that:
- \( P_r = \frac{P}{P_c} \)
- \( V_r = \frac{V}{V_c} \)
- \( T_r = \frac{T}{T_c} \)
From the problem, we have:
- \( \frac{P_c V_c}{R T_c} = \frac{3}{8} \) (Equation 1)
- \( \frac{P_r V_r}{T_r} = 2.21 \) (Equation 2)
Multiplying both equations gives:
\(
\frac{P_c V_c}{R T_c} \cdot \frac{P_r V_r}{T_r} = \frac{3}{8} \cdot 2.21
\)
Substituting the definitions into the equation:
\(
\frac{P_c V_c}{R T_c} \cdot \frac{P}{P_c} \cdot \frac{V}{V_c} \cdot \frac{T}{T_c} = \frac{3}{8} \cdot 2.21
\)
This simplifies to:
\(
\frac{PV}{RT} = \frac{3}{8} \cdot 2.21
\)
Calculate \( \frac{3}{8} \cdot 2.21 \):
\(
\frac{3 \cdot 2.21}{8} = 0.82875
\)
Using the ideal gas law, we can express the molar volume \( V_m \):
\(
V_m = \frac{RT}{P}
\)
Equating it to the previous result:
\(
\frac{PV}{RT} = 0.82875 \implies V = 0.82875 \cdot \frac{RT}{P}
\)
Using \( R = 0.0821 \, \text{L bar K}^{-1} \text{mol}^{-1} \), \( T = 200 \, K \), and converting \( P = 10.1325 \, \text{MPa} \) to bar:
\(
P = 10.1325 \times 10^6 \, \text{Pa} = \frac{10.1325 \times 10^6}{10^5} \, \text{bar} = 101.325 \, \text{bar}
\)
Now substituting the values into the equation:
\(
V = 0.82875 \cdot \frac{0.0821 \cdot 200}{101.325}
\)
Calculating:
\(
V = 0.82875 \cdot \frac{16.42}{101.325} \approx 0.82875 \cdot 0.162 \approx 0.134 \, \text{L}
\)
Since we have 2.0mol of N₂, the total volume is:
\(
V_{total} = 2 \cdot 0.134 \approx 0.268 \, \text{L} = 268 \, \text{mL}
\)
The volume occupied by 2.0mol of N₂ at 200K and 10.1325MPa is approximately 268 mL.
Topper's Solved these Questions
- STATES OF MATTERBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STATES OF MATTEREXERCISE - Illustration
2 Videos
- STATES OF MATTERBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STATES OF MATTEREXERCISE - Exercises
21 Videos
- SOME BASIC CONCEPTS AND MOLE CONCEPTBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOME BASIC CONCEPTS AND MOLE CONCEPTEXERCISE - Archives Subjective
11 Videos
- STOICHIOMETRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STOICHIOMETRYEXERCISE - Archives Subjective
33 Videos
Similar Questions
Calculate the volume occupied by 2.0 mole of N2at200K and 8.21atm pressure, if PCVCRTC=38 and PrVrTr=2.4.
View SolutionCalculate the volume occupied by 16gram O2 at 300K and 8.31Mpa if PCVCRTC=3/8 and PrVrTr=2.21 ( Given :R=8.314MPa/K−mol)
View SolutionCalculate the volume occupied by 8.8 g of CO2 at 31.1∘C and 1 bar pressure. R= 0.083 bar L K−1mol−1.
View SolutionThe volume of 2.8g of CO at 27∘C and 0.821atm pressure is (R=0.0821 lit. atm mol−1K−1)
View SolutionAt low pressure, if RT=2√a.p, then the volume occupied by a real gas is :
(a)2RTP
(b)2PRT
(c)RT2P
(d)2RTP
View SolutionUsing the van der Waals equation, calculate the pressure of 10.0molNH3 gas in a 10.0L vessel at 27∘C.
(P+n2aV2)(V−nb)=nRTa=4.2L2.atm/mol2b=0.037L/mol
View SolutionAt low pressure, the van der Waal's equation become :
(a)PVm=RT
(b)P(Vm−b)=RT
(c)(P+aV2M)Vm=RT
(d)P=RTVm+aV2m
View SolutionIf .nPr=720 and .nCr=120, then find r.
.
View Solutionif .2nC2:nC2=9:2and.nCr=10, then r is equal to
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
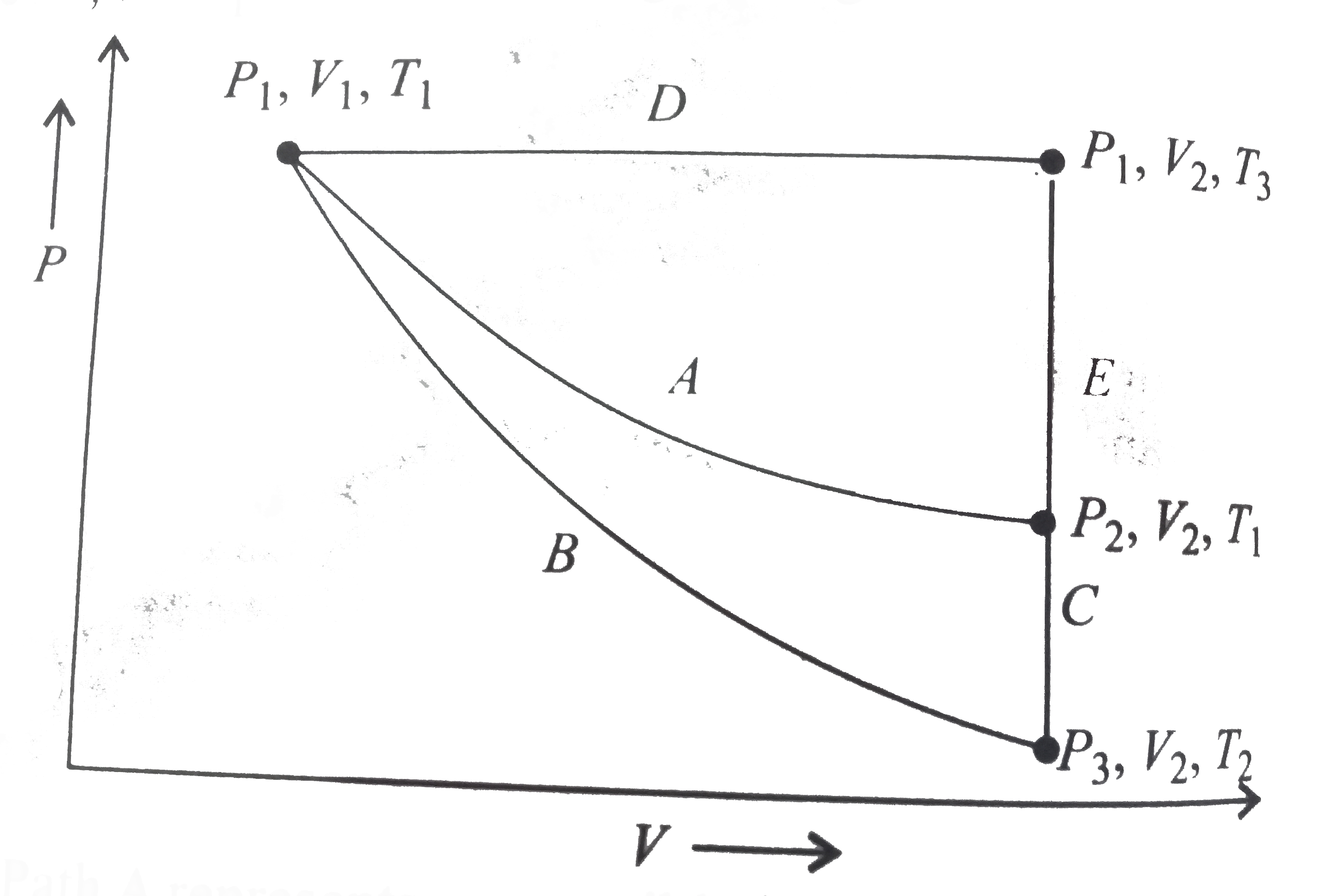
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is ΔS for path (D+E)?
View Solution