A gas- filled freely collapsible balloon is pushed from the surface level of a lake to a depth of . Approximately what percentage of its original volume will the balloon finally have? Assume that the gas behaves ideally
To solve the problem of determining the percentage of the original volume of a gas-filled freely collapsible balloon when pushed to a depth of 100 m in a lake, we can follow these steps:
Step 1: Understand the situation
A gas-filled balloon is submerged in water, and as it is pushed deeper, the pressure on the balloon increases. According to Boyle's Law, the volume of a gas is inversely proportional to the pressure when temperature is constant.
Step 2: Identify initial and final conditions
- Initial Volume (V1): The volume of the balloon at the surface (let's denote it as V).
- Final Volume (V2): The volume of the balloon at a depth of 100 m.
Step 3: Calculate the pressures
- Pressure at the surface (P1): This is equal to atmospheric pressure, which is approximately 1 atmosphere (atm).
- Pressure at a depth (P2): The pressure at a depth can be calculated using the formula:
P2=P1+(density of water)×g×h
where:
- Density of water (ρ) = 1 g/cm³ = 1000 kg/m³
- g (acceleration due to gravity) = 9.81 m/s²
- h (depth) = 100 m
Step 4: Convert units and calculate P2
Convert the pressure at the surface to consistent units (Pascals):
P1=1 atm=101325 Pa
Now calculate the pressure at 100 m depth:
P2=101325 Pa+(1000 kg/m3)×(9.81 m/s2)×(100 m)
P2=101325 Pa+981000 Pa=1081325 Pa
Step 5: Apply Boyle's Law
According to Boyle's Law:
P1⋅V1=P2⋅V2
Substituting the known values:
101325⋅V=1081325⋅V2
Step 6: Solve for V2
Rearranging the equation gives:
V2=1013251081325⋅V
Step 7: Calculate the percentage of original volume
To find the percentage of the original volume:
Percentage=(V2V)×100%
Substituting for V2:
Percentage=(1013251081325)×100%
Calculating this gives:
Percentage≈9.36%
Final Answer
Approximately 9.36% of the original volume will remain when the balloon is at a depth of 100 m.
---
A gas-filled balloon is submerged in water, and as it is pushed deeper, the pressure on the balloon increases. According to Boyle's Law, the volume of a gas is inversely proportional to the pressure when temperature is constant.
- Initial Volume (V1): The volume of the balloon at the surface (let's denote it as V).
- Final Volume (V2): The volume of the balloon at a depth of 100 m.
- Pressure at the surface (P1): This is equal to atmospheric pressure, which is approximately 1 atmosphere (atm).
- Pressure at a depth (P2): The pressure at a depth can be calculated using the formula:
P2=P1+(density of water)×g×h
where:
- Density of water (ρ) = 1 g/cm³ = 1000 kg/m³
- g (acceleration due to gravity) = 9.81 m/s²
- h (depth) = 100 m
Convert the pressure at the surface to consistent units (Pascals):
P1=1 atm=101325 Pa
Now calculate the pressure at 100 m depth:
P2=101325 Pa+(1000 kg/m3)×(9.81 m/s2)×(100 m)
P2=101325 Pa+981000 Pa=1081325 Pa
According to Boyle's Law:
P1⋅V1=P2⋅V2
Substituting the known values:
101325⋅V=1081325⋅V2
Rearranging the equation gives:
V2=1013251081325⋅V
To find the percentage of the original volume:
Percentage=(V2V)×100%
Substituting for V2:
Percentage=(1013251081325)×100%
Calculating this gives:
Percentage≈9.36%
Approximately 9.36% of the original volume will remain when the balloon is at a depth of 100 m.
Topper's Solved these Questions
- STATES OF MATTERBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STATES OF MATTEREXERCISE - Illustration
2 Videos
- STATES OF MATTERBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STATES OF MATTEREXERCISE - Exercises
21 Videos
- SOME BASIC CONCEPTS AND MOLE CONCEPTBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOME BASIC CONCEPTS AND MOLE CONCEPTEXERCISE - Archives Subjective
11 Videos
- STOICHIOMETRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STOICHIOMETRYEXERCISE - Archives Subjective
33 Videos
Similar Questions
Knowledge Check
A mass of ideal gas at pressure P is expanded isothermally to four times the originl volume and then slowly compressed adiabatically to its original volume. Assuming γ to be 1.5 , the new pressure of the gas is
A0.58333333333333BPC0.66666666666667DP/2
A monoatomic gas at pressure P1 and volume V1 is compressed adiabatically to 18th of its original volume. What is the final pressure of gas.
View SolutionAn observer having a gun observes a remotely controlled balloon. When he first noticed the balloon, it was at an altitude of 800m and moving vertically upward at a constant velocity of 5m/s. The horizontal displacement of balloon from the observer is 1600m. Shells fired from the gun have an initial velocity of 400m/s at a fixed angle θ(sinθ=3/5and cosθ=4/5). The observer having gun waits ( for some time after observing the balloon ) and fires so as to destroy the balloon. Assume g=10m/s2. Neglect air resistance.
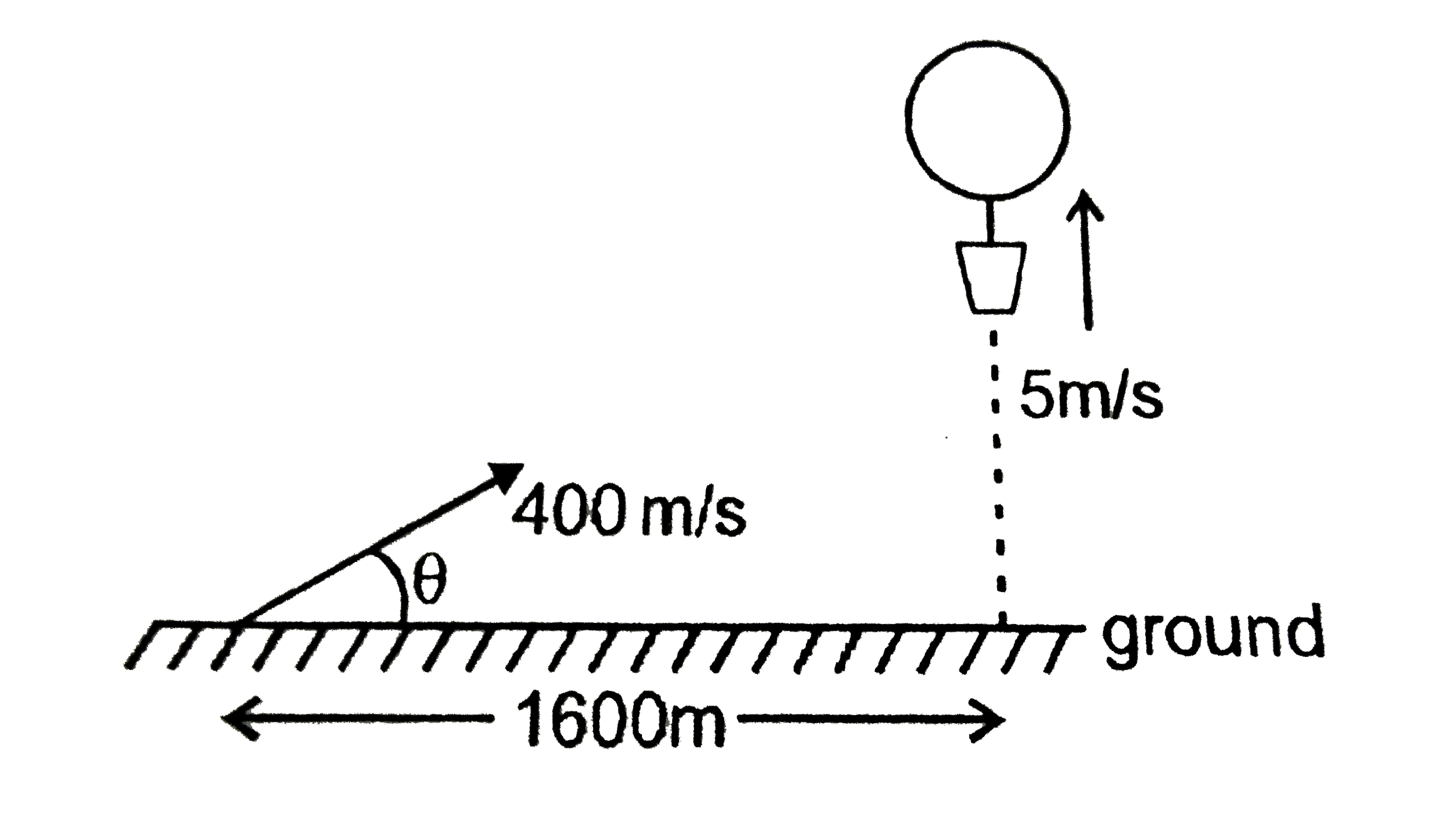
The altitude of the collosion above ground level is
View SolutionA conducting bolloon of the radius a is charged to potential V0 and held at a large height above the earth ensures that charge distribution on the surface of the balloon remains unaffected by the presence of the earth. It is connected to the earth through a resistance R and a value in the balloon is opened . The gas inside the balloon escapes from value and the size of the balloon decreases. The rate of decrease in radius of the balloon is controlled in such a manner that potential of the balloon remains constant. Assume the electric permittivity of the surrounding air equals to that of free space (ε0) and charge cannot leak to the surrounding air.
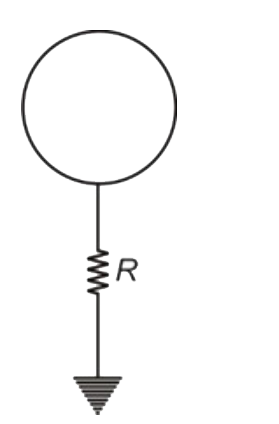
The rate at which radius r of the balloon changes with time is best represented by the equation
View SolutionFour moles of an ideal gas at a pressure of 4 atm and at a temperature of 70∘C expands is othermally to four times its initial volume : What is (i) the final temperature and (ii) the final volume ?
View SolutionIn taking a solid ball of rubber from the surface to the bottom of a lake of 180m depth, reduction in the volume of the ball is 0.01%. The density of water of the lake is 1×103kg/m3. Determine the value of the bulk modulus of elasticity of rubber . (g=9.8m/s2)
View SolutionA sample of an ideal gas has pressure p0, volume V0 and tempreture T0. It is isothermally expanded to twice its oringinal volume.it is then compressed at constant pressure to have the original volume V0. Finally, the gas is heated at constant volume to get the original tempreture.(a) show the process in a V-T diagram (b) calculate the heat absorbed in the process.
View SolutionA balloon which is initially collapsed and flat is slowly filled with a gas at 100kPa so as to form it into a sphere of 1m radius.The work done by the gas in the balloon during the filling process is
View Solution
