A flask contains each of and at . After equilibrium was reached, partial pressure of was . At this point, of was injected and gas mixture was cooled to . Find out the gas pressure.
To solve the problem step-by-step, let's break it down into manageable parts.
Step 1: Determine Initial Conditions
We start with a 100 dm³ flask containing 10 moles each of N2 and H2 at 700 K.
Step 2: Calculate the Partial Pressure of H2
Using the ideal gas law, we can calculate the partial pressure of H2 at equilibrium:
PV=nRT
Where:
- P = pressure (in atm)
- V = volume (in dm³)
- n = number of moles
- R = ideal gas constant = 0.0821 L·atm/(K·mol)
- T = temperature (in K)
Rearranging the equation gives:
P=nRTV
Substituting the values for H2:
PH2=10mol×0.0821L⋅atm/(K⋅mol)×700K100dm3
Calculating this gives:
PH2=574.7100=5.747atm
Step 3: Establish Equilibrium Conditions
At equilibrium, the partial pressure of H2 is given as 1 atm. This indicates that some H2 has reacted to form ammonia (NH3). The reaction is:
N2+3H2→2NH3
Let x be the amount of H2 that reacted. Thus:
- Moles of H2 at equilibrium = 10−3x
- Moles of N2 at equilibrium = 10−x
- Moles of NH3 formed = 2x
Given that the equilibrium moles of H2 is 1 atm, we can set up the equation:
10−3x=1⟹3x=9⟹x=3
Step 4: Calculate Moles of N2 at Equilibrium
Substituting x back:
Moles of N2=10−x=10−3=7moles
Step 5: Calculate Total Moles at Equilibrium
Total moles at equilibrium:
Total moles=(10−3)+(10−3)+2(3)=7+1+6=14moles
Step 6: Inject Water and Adjust Volume
5 L of H2O is injected into the system, reducing the volume of gas:
New Volume=100dm3−5L=95dm3
Step 7: Cool the Mixture to 298 K
Now we need to calculate the pressure at the new conditions (95 dm³ and 298 K):
Using the ideal gas law again:
P=nRTV
Substituting the values:
P=14moles×0.0821L⋅atm/(K⋅mol)×298K95dm3
Calculating this gives:
P=341.495≈3.59atm
Final Answer
The final pressure of the gas mixture is approximately 3.59 atm.
---
We start with a 100 dm³ flask containing 10 moles each of N2 and H2 at 700 K.
Using the ideal gas law, we can calculate the partial pressure of H2 at equilibrium:
PV=nRT
Where:
- P = pressure (in atm)
- V = volume (in dm³)
- n = number of moles
- R = ideal gas constant = 0.0821 L·atm/(K·mol)
- T = temperature (in K)
P=nRTV
PH2=10mol×0.0821L⋅atm/(K⋅mol)×700K100dm3
Calculating this gives:
PH2=574.7100=5.747atm
At equilibrium, the partial pressure of H2 is given as 1 atm. This indicates that some H2 has reacted to form ammonia (NH3). The reaction is:
N2+3H2→2NH3
- Moles of H2 at equilibrium = 10−3x
- Moles of N2 at equilibrium = 10−x
- Moles of NH3 formed = 2x
10−3x=1⟹3x=9⟹x=3
Substituting x back:
Moles of N2=10−x=10−3=7moles
Total moles at equilibrium:
Total moles=(10−3)+(10−3)+2(3)=7+1+6=14moles
5 L of H2O is injected into the system, reducing the volume of gas:
New Volume=100dm3−5L=95dm3
Now we need to calculate the pressure at the new conditions (95 dm³ and 298 K):
Using the ideal gas law again:
P=nRTV
Substituting the values:
P=14moles×0.0821L⋅atm/(K⋅mol)×298K95dm3
Calculating this gives:
P=341.495≈3.59atm
The final pressure of the gas mixture is approximately 3.59 atm.
Topper's Solved these Questions
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STATES OF MATTEREXERCISE - Illustration2videos
STATES OF MATTER
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STATES OF MATTEREXERCISE - Exercises21videos
STATES OF MATTER
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOME BASIC CONCEPTS AND MOLE CONCEPTEXERCISE - Archives Subjective11videos
SOME BASIC CONCEPTS AND MOLE CONCEPT
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STOICHIOMETRYEXERCISE - Archives Subjective33videos
STOICHIOMETRY
Similar Questions
11 moles of N2 and 12 moles of H2 mixture reacted in 2.0 litre vessel at 800 K. After equilibrium was reached, 6 mole of H2 was present. 3.58 litre of liquid water is injected in equibrium mixture and resultant gaseous mixture suddenly cooled to 300K. What is the final pressure of gaseous mixture? Neglect vapour pressure of liquid solution. Assume (i) all NH3 dissolved in water (ii) no change in volume of liquid (iii) At 300 K no reaction takes place between N2 and H2
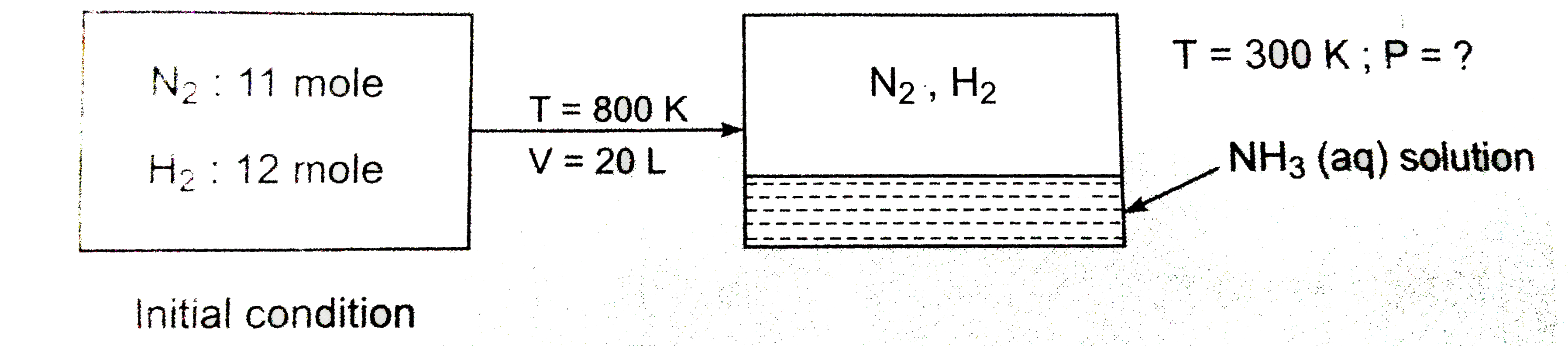
(a)18.47 atm
(b)60 atm
(c)22.5 atm
(d)45 atmView SolutionThe partial pressure of hydrogen in a flask containing 2 g of H2 and 32 g of SO2 is
View Solution1 gram H2 and 8g O2 were taken in a 10 liter vessel at 300 K. The partial pressure exerted by O2 will be
View Solution821mLN2(g) was collected over liquid water at 300 K and 1 atm.If vapour pressure of H2O is 30 torr then moles of N2(g) in moist gas mixture is :
View SolutionA 10L flask at 298K contains a gaseous mixture of CO and CO2 at a total pressure of 2.0bar if 0.20 mole of CO is present, find its partial pressure and also that of CO2.
View SolutionA 2.5L flask contains 0.25mol each of sulphur dioxide and nitrogen gas at 27∘C. Calculate the partial pressure exerted by each gas and also the total pressure.
View SolutionA mixture of one mole of each of O2(g),H2(g), He(g) exists in a container of volume V at temperatureT in which partial pressure of H2 (g) is 2atm. the total pressure in the container is:
View SolutionA mixture of one mole of each of O2(g),H2(g), He(g) exists in a container of volume V at temperatureT in which partial pressure of H2 (g) is 2atm. the total pressure in the container is:
View SolutionA gaseous mixture contains 1 g of H2 , 4 g of He , 7 g of N2 and 8 g of O2 . The gas having the highest partial pressure is :-
View SolutionA sample of HI(g) is placed in flask at a pressure of 0.2atm. At equilibrium. The partial pressure of HI(g) is 0.04atm. What is Kp for the given equilibrium?
2HI(g)⇔H2(g)+I2(g)View Solution

