An ideal gas undergoes isothermal expansion followed by heat removel at constant volume and they by heat removal at constant pressure to the initial volume. The correct descripion of these steps is indicated by
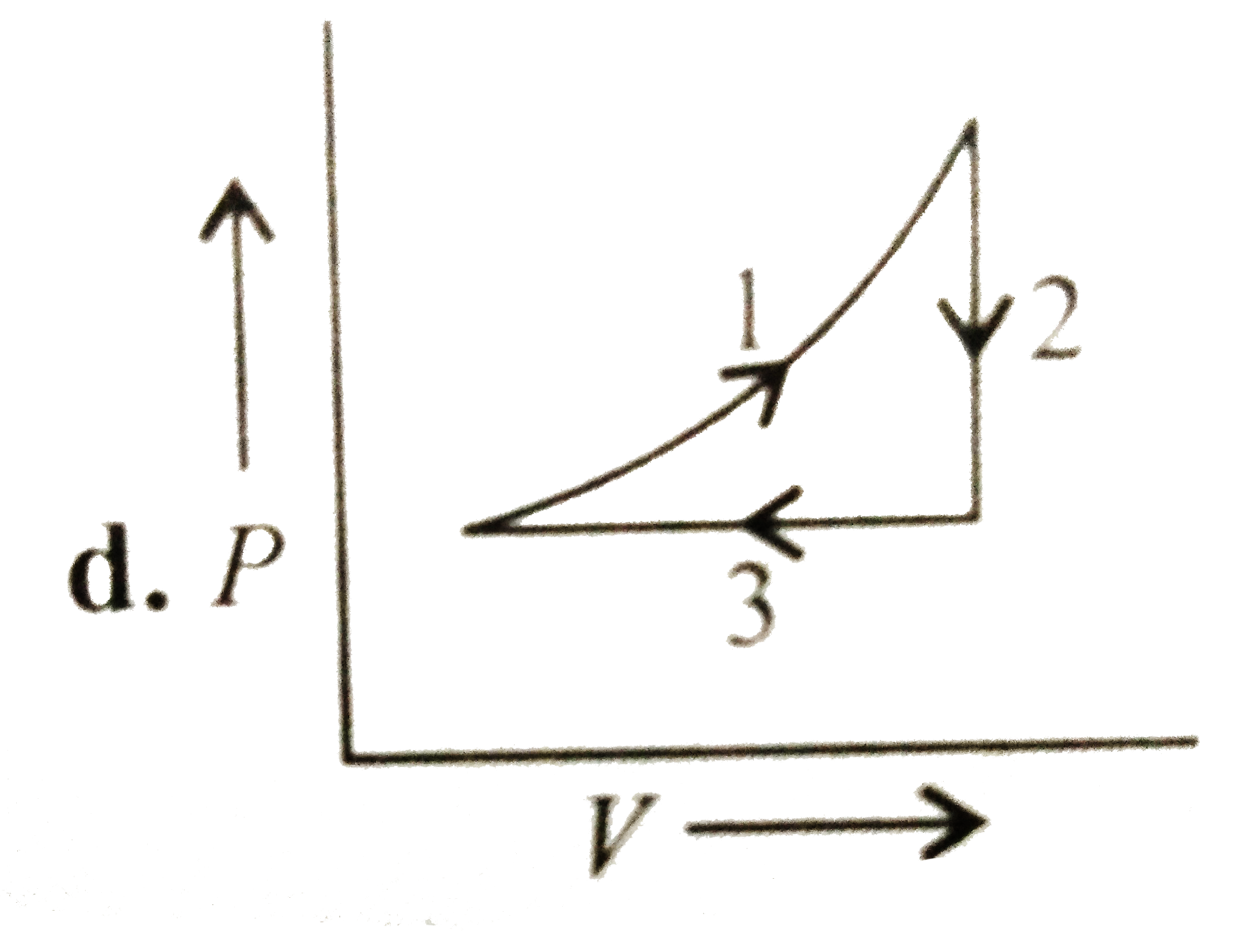
The correct Answer is:D
To solve the problem of an ideal gas undergoing isothermal expansion followed by heat removal at constant volume and then heat removal at constant pressure back to the initial volume, we can break down the process into three steps and analyze each one.
Step 1: Isothermal Expansion
- In this step, the gas expands isothermally. For an ideal gas, during an isothermal process, the temperature (T) remains constant. According to the ideal gas law (PV = nRT), if the temperature is constant and the volume increases, the pressure must decrease.
- The relationship between pressure (P) and volume (V) during this process can be represented as a hyperbola on a PV diagram. This means that as the volume increases, the pressure decreases, maintaining the product PV constant.
Step 2: Heat Removal at Constant Volume
- In this step, heat is removed from the gas while keeping the volume constant. Since the volume does not change, the work done (W) is zero (W = PΔV = 0).
- However, when heat is removed, the internal energy of the gas decreases, which leads to a decrease in temperature. According to the ideal gas law, if the temperature decreases while the volume remains constant, the pressure must also decrease.
Step 3: Heat Removal at Constant Pressure
- In the final step, heat is removed from the gas at constant pressure. When heat is removed at constant pressure, the volume of the gas will decrease as the temperature decreases (since P is constant).
- This means that the process will show a linear relationship on a PV diagram, where the pressure remains constant while the volume decreases.
Summary of the Steps:
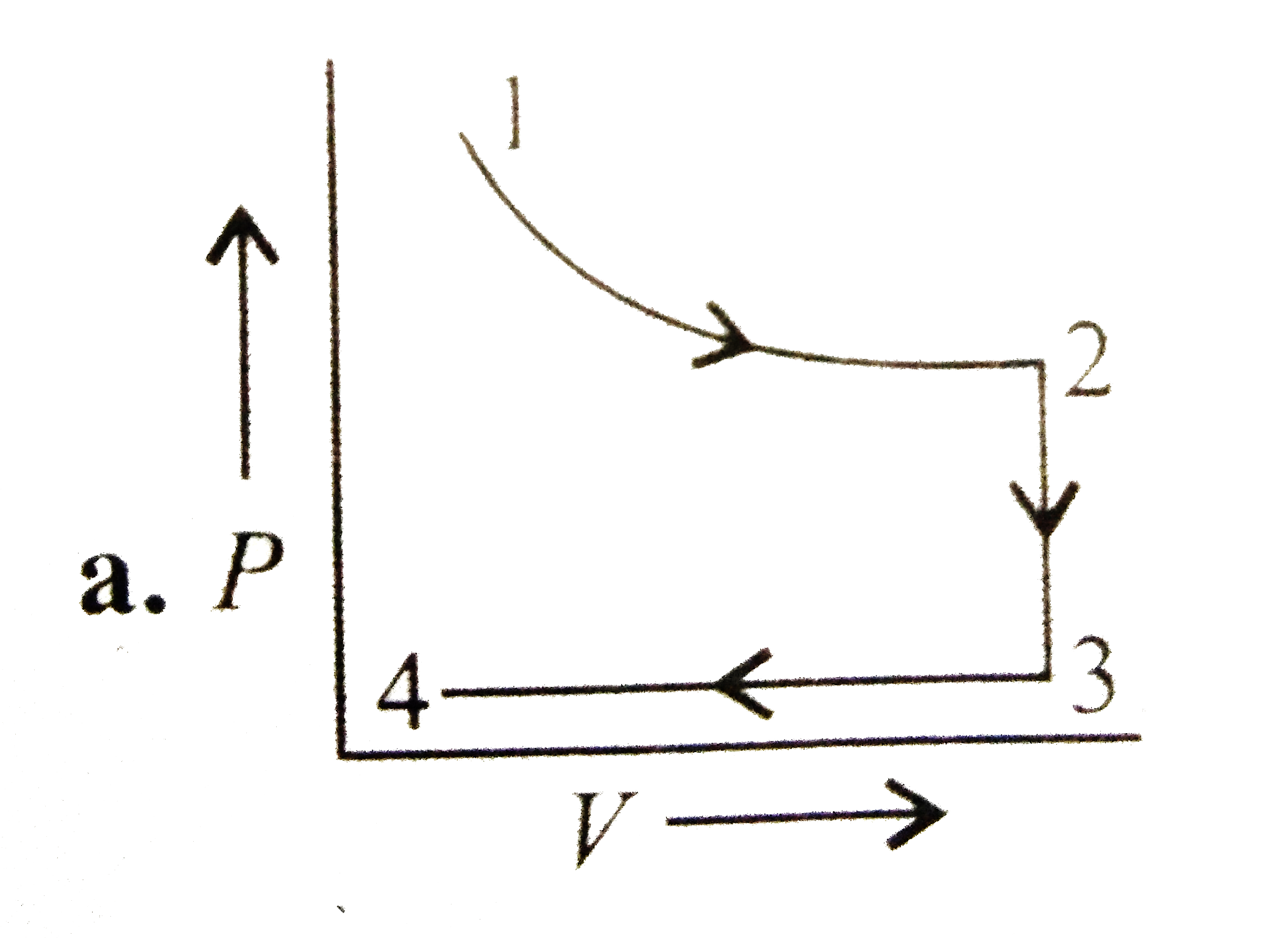
1. Isothermal Expansion: Pressure decreases as volume increases (hyperbolic curve).
2. Heat Removal at Constant Volume: Pressure decreases as temperature decreases (vertical line downwards).
3. Heat Removal at Constant Pressure: Volume decreases as temperature decreases (horizontal line leftwards).
Conclusion:
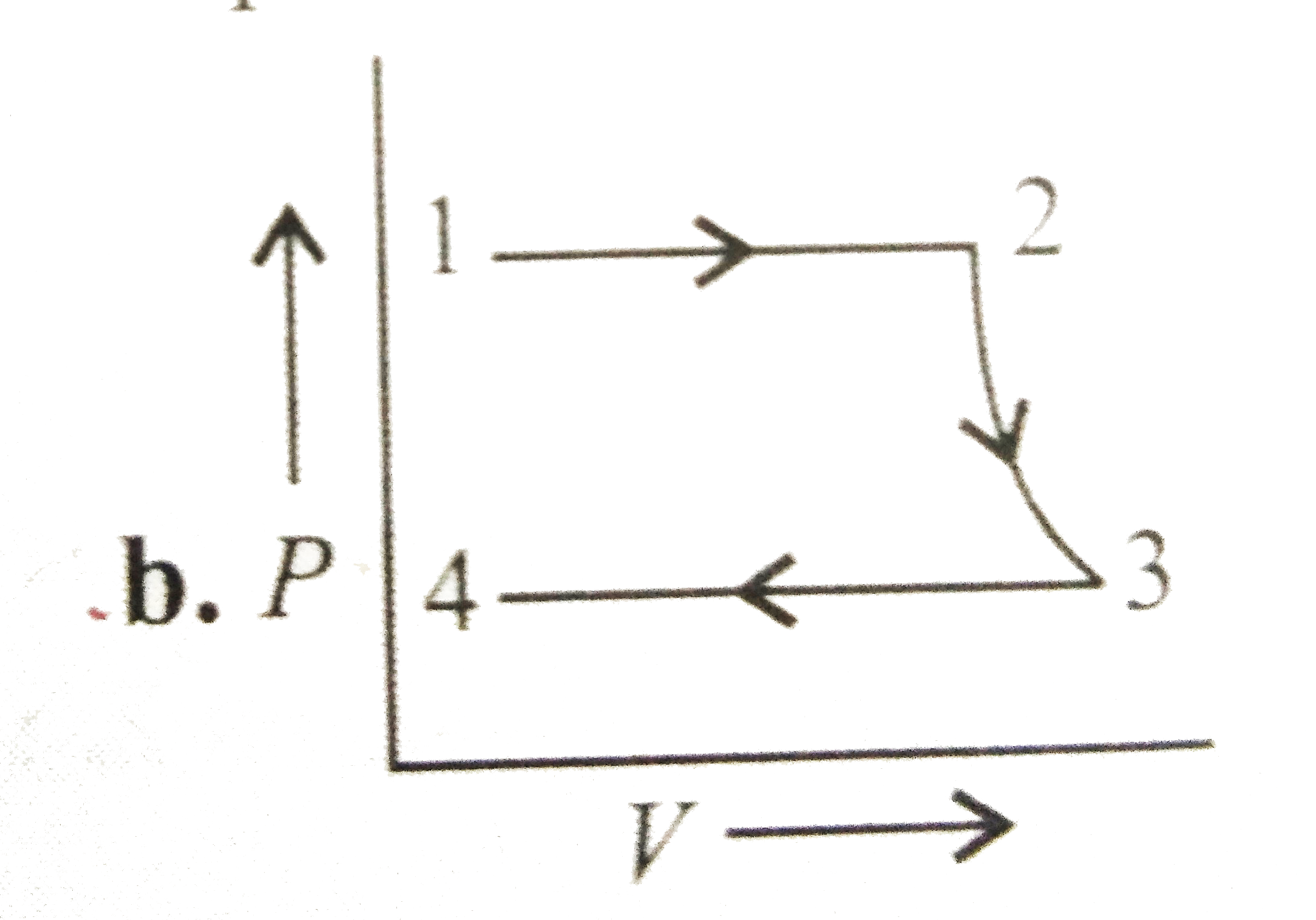
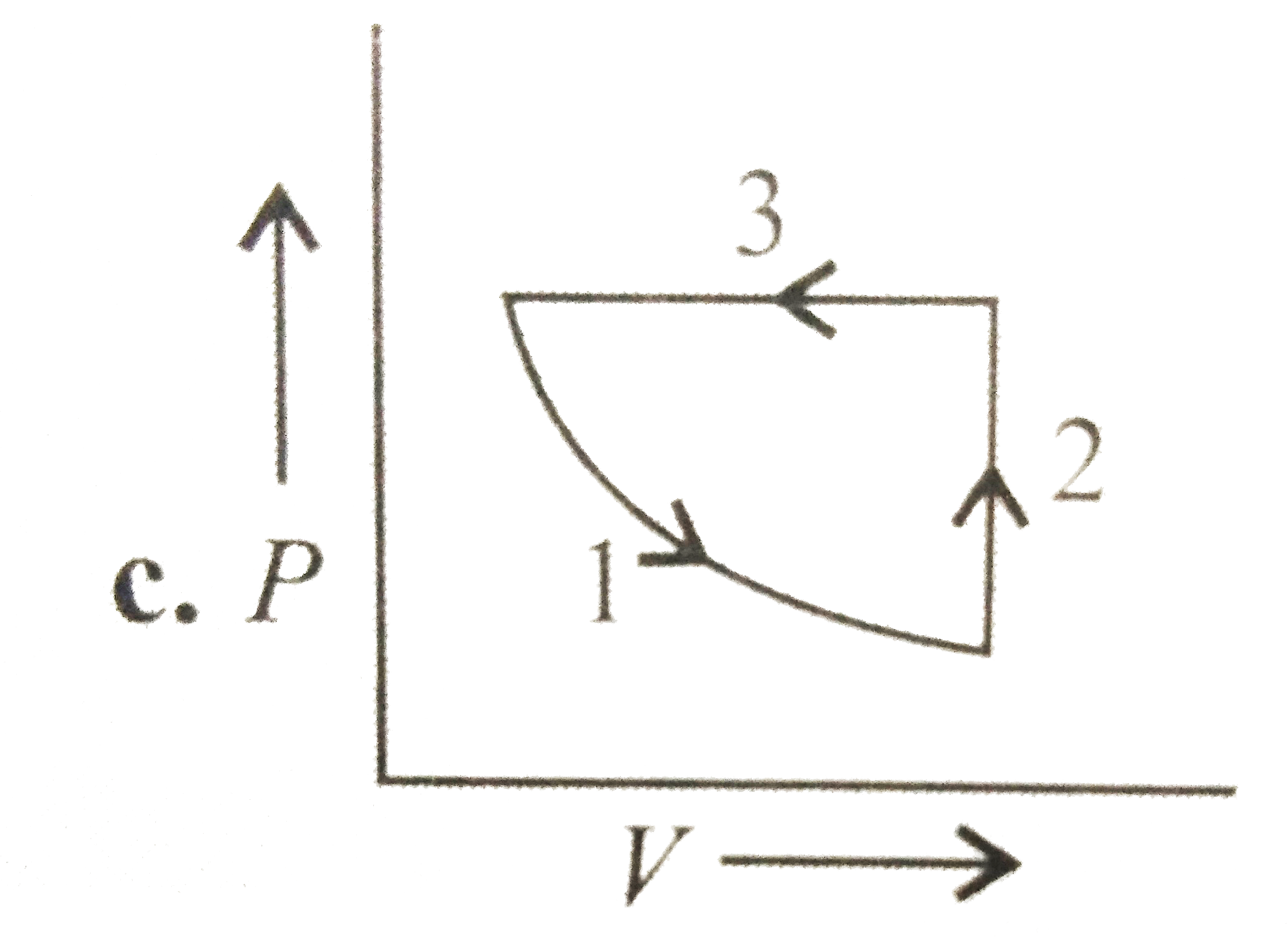
The correct description of these steps can be represented graphically on a PV diagram, where the first step is a hyperbola, the second step is a vertical line (constant volume), and the third step is a horizontal line (constant pressure). The correct option that matches this description is Option A.
- In this step, the gas expands isothermally. For an ideal gas, during an isothermal process, the temperature (T) remains constant. According to the ideal gas law (PV = nRT), if the temperature is constant and the volume increases, the pressure must decrease.
- The relationship between pressure (P) and volume (V) during this process can be represented as a hyperbola on a PV diagram. This means that as the volume increases, the pressure decreases, maintaining the product PV constant.
- In this step, heat is removed from the gas while keeping the volume constant. Since the volume does not change, the work done (W) is zero (W = PΔV = 0).
- However, when heat is removed, the internal energy of the gas decreases, which leads to a decrease in temperature. According to the ideal gas law, if the temperature decreases while the volume remains constant, the pressure must also decrease.
- In the final step, heat is removed from the gas at constant pressure. When heat is removed at constant pressure, the volume of the gas will decrease as the temperature decreases (since P is constant).
- This means that the process will show a linear relationship on a PV diagram, where the pressure remains constant while the volume decreases.
1. Isothermal Expansion: Pressure decreases as volume increases (hyperbolic curve).
2. Heat Removal at Constant Volume: Pressure decreases as temperature decreases (vertical line downwards).
3. Heat Removal at Constant Pressure: Volume decreases as temperature decreases (horizontal line leftwards).
The correct description of these steps can be represented graphically on a PV diagram, where the first step is a hyperbola, the second step is a vertical line (constant volume), and the third step is a horizontal line (constant pressure). The correct option that matches this description is Option A.
Topper's Solved these Questions
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Ex 6.3
27 Videos
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Ex 6.4
16 Videos
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Ex 6.1
26 Videos
- STOICHIOMETRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STOICHIOMETRYEXERCISE - Archives Subjective
33 Videos
Similar Questions
Knowledge Check
The ratio of the molar heat capacities of a diatomic gas at constant pressure to that at constant volume is
A75B32C35D52An ideal gas having molar specific heat capaicty at constatnt volume is 32R, the molar specific heat capacities at constant pressure is
A12RB52RC72RD92R
For an ideal gas, the heat of reaction at constant pressure and constant volume are related as
View SolutionHeat supplied to an ideal gas sample at constant Pressure :
View SolutionIf a gas is heated at constant pressure, its isothermal compressibility
View SolutionA perfect gas at 27∘C is heated at constant pressure so as to triple its volume. The tmemperature of th gas will be
View SolutionA perfect gas at 27∘C is heated at constant pressure so as to duble its volume. The tmemperature of th gas will be
View SolutionA perfect gas at 27∘C is heated at constant pressure so as to triple its volume. The tmemperature of th gas will be
View Solution
