The pressure -temperature (P−T) phase diagram shown below corresponds to the
a. Curve of fusion of solids that expand on solidification.
b. Curve of sublimation of solids that directly go over to the vapour phase.
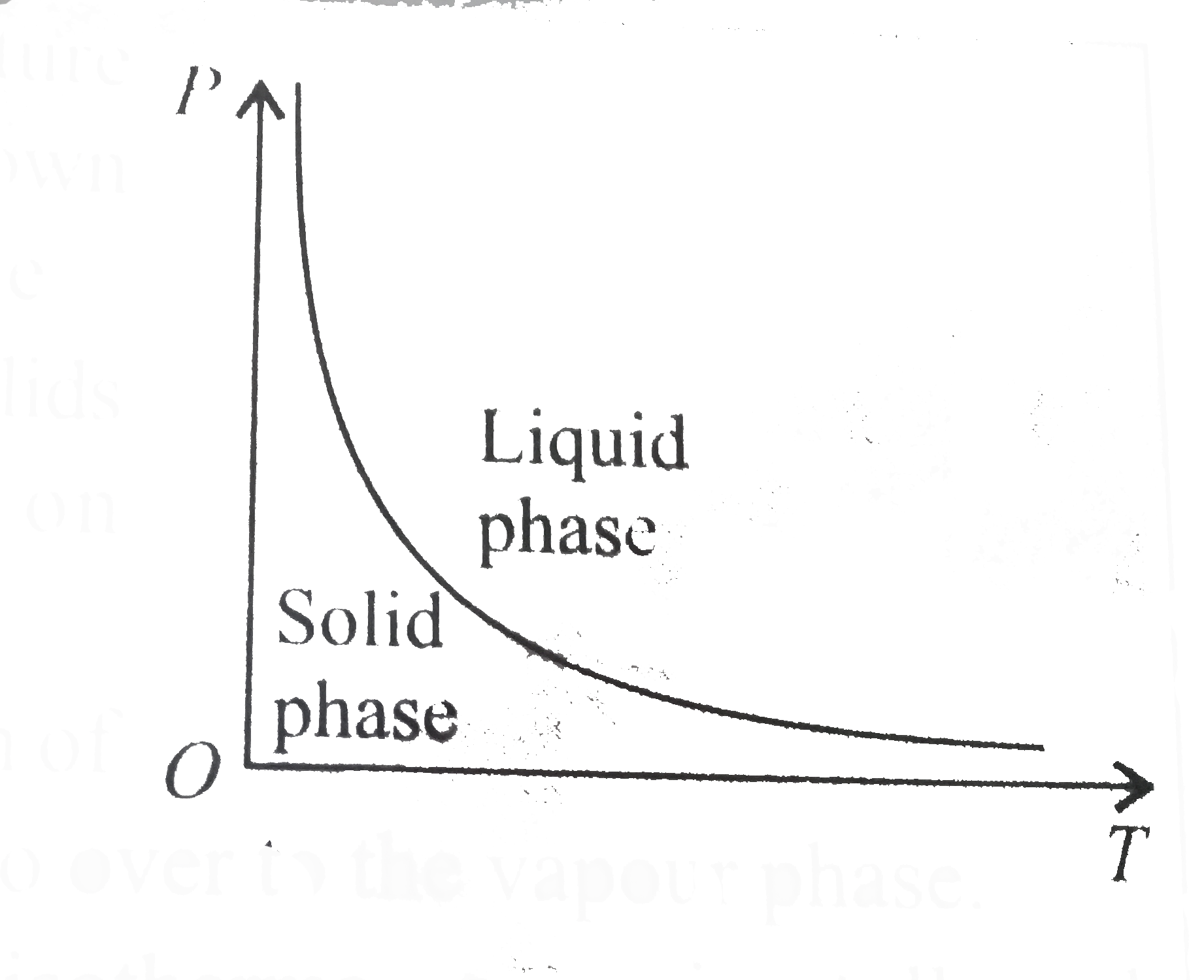
Step by step video & image solution for The pressure -temperature (P-T) phase diagram shown below corresponds to the a. Curve of fusion of solids that expand on solidification. b. Curve of sublimation of solids that directly go over to the vapour phase. by Chemistry experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Ex 6.3
27 Videos
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Ex 6.4
16 Videos
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Ex 6.1
26 Videos
- STOICHIOMETRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STOICHIOMETRYEXERCISE - Archives Subjective
33 Videos
Similar Questions
Each phase of a material can exits only in certain regions of pressure and temperature . P−T phase diagrams, in which pressure is plotted versus temperature, show the regions corresponding to various phases and phase transformations . P−V diagrams, on the other hand , can be used to study pressure volume relationship at a constant temperature.
If the liquid and gaseous phases of a pure substances are heated together in a closed container, both the temperature and the vapor pressure will increase until a point is reached at which the two phases can no longer be distinguished from one another. The temperature and pressure at which this occurs are called the critical temperature and pressure. Exceeding either of these parameters, by itself ,will cause the gas/liguid phase transition to disappear. if the other variable is then changed as well, while the first variable is maintained above its critical point , a gradual transition will occur between the gaseous and liquid phases, with no clear boundary.(The liquid and solid phases, on the other hand , maintain a distinct boundary at all pressure above the triple point). Shown in figure is a combined P−T phase diagram for material A and B.
_E01_195_Q01.png)
If heat is added to solids A and B , each in a container that is open to the atmosphere :-
View SolutionEach phase of a material can exits only in certain regions of pressure and temperature . P−T phase diagrams, in which pressure is plotted versus temperature, show the regions corresponding to various phases and phase transformations . P−V diagrams, on the other hand , can be used to study pressure volume relationship at a constant temperature.
If the liquid and gaseous phases of a pure substances are heated together in a closed container, both the temperature and the vapor pressure will increase until a point is reached at which the two phases can no longer be distinguished from one another. The temperature and pressure at which this occurs are called the critical temperature and pressure. Exceeding either of these parameters, by itself ,will cause the gas/liguid phase transition to disappear. if the other variable is then changed as well, while the first variable is maintained above its critical point , a gradual transition will occur between the gaseous and liquid phases, with no clear boundary.(The liquid and solid phases, on the other hand , maintain a distinct boundary at all pressure above the triple point). Shown in figure is a combined P−T phase diagram for material A and B.
_E01_196_Q01.png)
Which is true about the substance in figure?
View SolutionOn a phase diagram draw the fusion curve, vaporisation curve and sublimation curve. Define triple point.
View SolutionThe vapour pressure curves of the same solute in the same solvent are shown below. The curves are parallel to each other andnot intersectt. The concentrations of solutions are in order of :
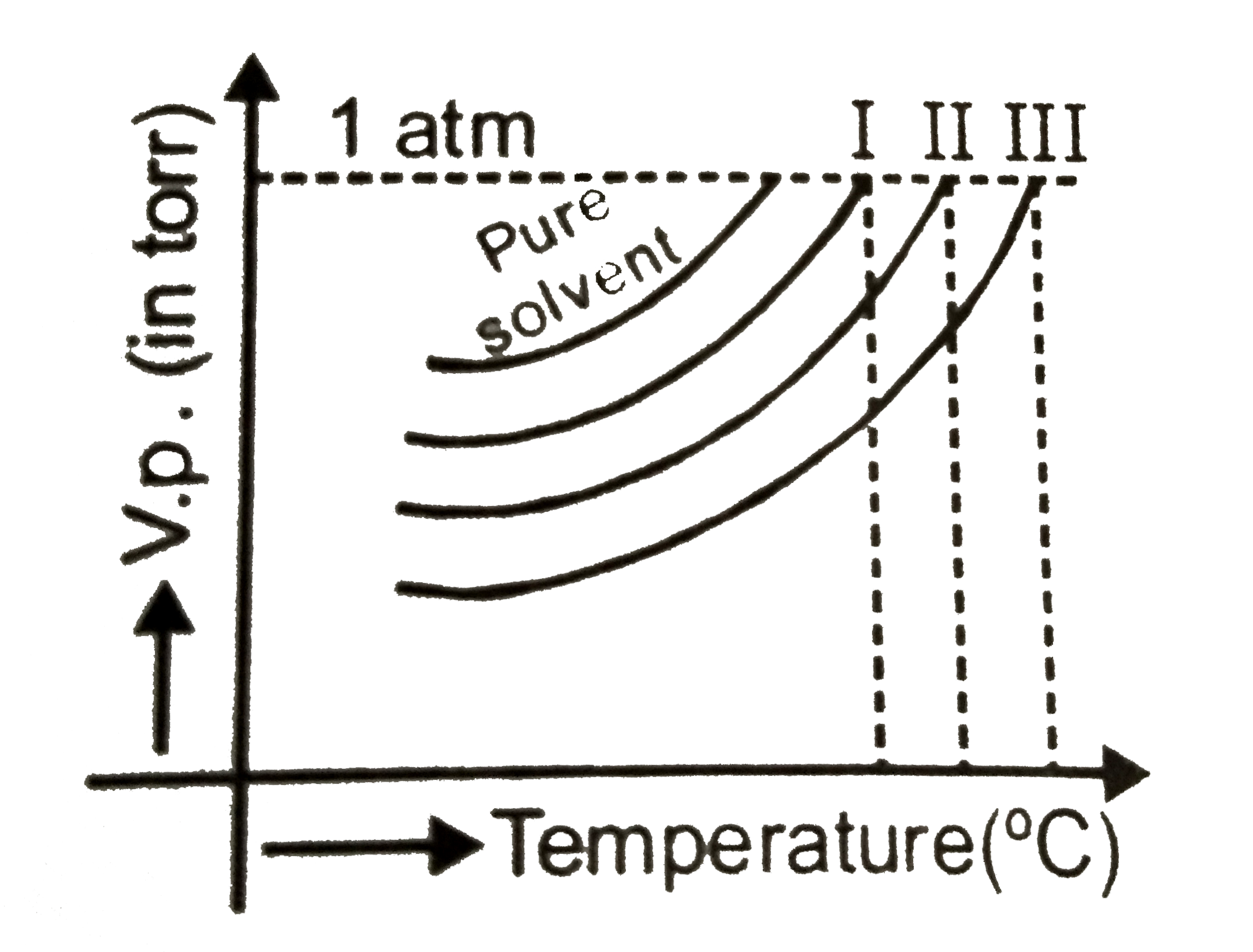
View SolutionAnswer the question (given below) which are based on the following diagra.
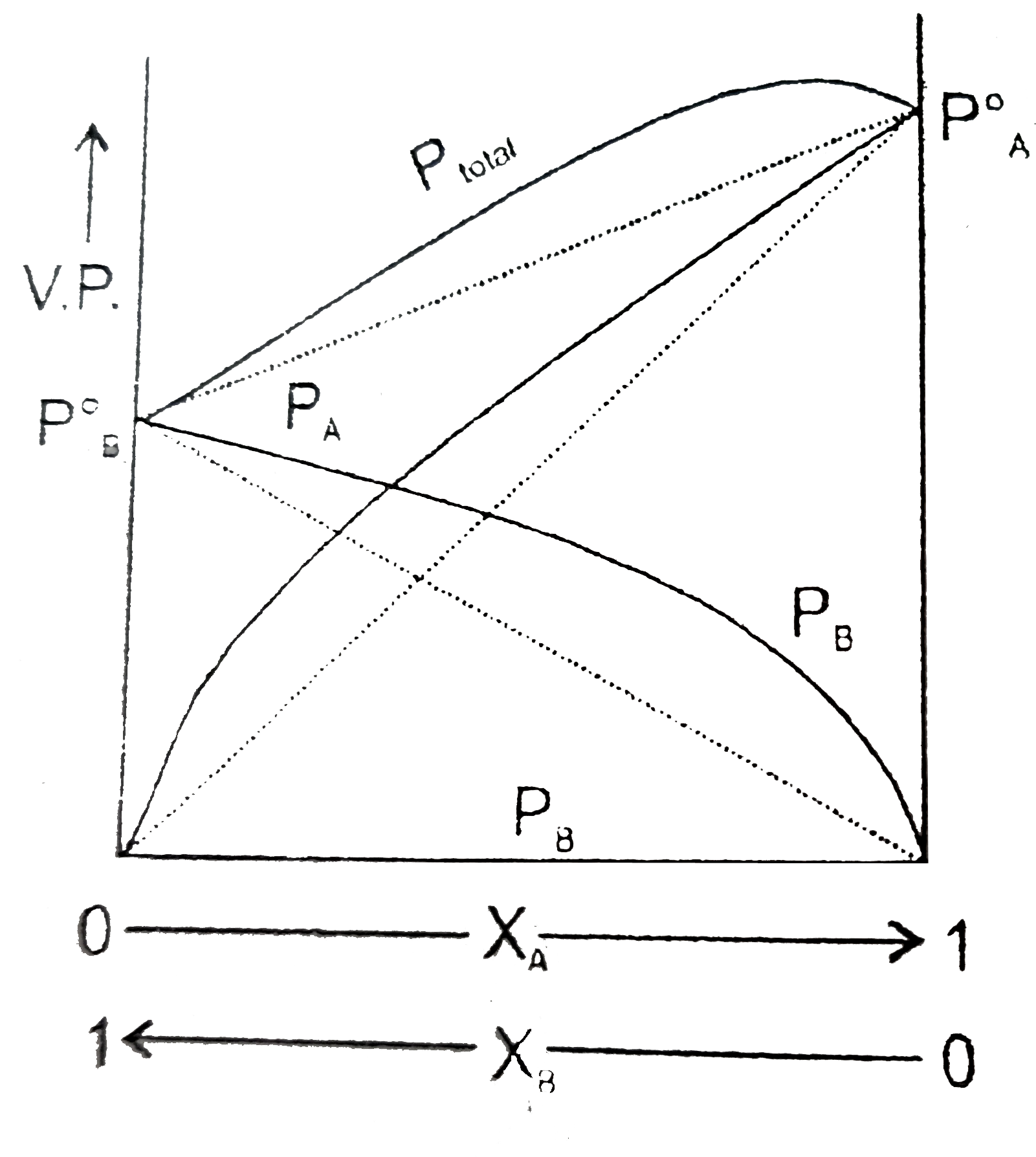
Consider some facts about the above phase diagram :
Vapour pressure diagram for real solutions of two liquids A and B that exhibit a positive deviation from Raoult's law. The vapour pressure of both A and B are greater than predicted by Raoult's law. The dashed lines lines represented the plots for ideal solutions.
Total vapour pressure of mixture of 1 mol of volatile component A(P∘A=100mmHg) and 3 mol of volatile component B(P∘B=60mmHg) is 75mm. For such case:
View SolutionSolids and liquids both expands on heating. The density of substance decreases on expanding according to the relation ρ2=ρ11+γ(T2−T1), where , ρ1→density atT1,ρ2→density atT2,γ→ coefficient of volume expansion of substances. When a solid is submerged in a liquid , liquid exerts an upward force on solid which is equal to the weight of liquid displaced by submerged part of solid. Solid will float or sink depends on relative densities of solid and liquid . A cubical block of solid floats in a liquid with half ot its volume submerged in liquid as shown in figure (at temperature T) αS→ Coefficient of linear expansion of solid
γL→Coefficient of volume expansion of liquid
ρS→Density of solid at temperatureT
ρL→ Density of liquid at temperatureT
_E01_201_Q01.png)
Assume block does not expand on heating . The temperature at which the block just begins to sink in liquid is
View SolutionSolids and liquids both expands on heating. The density of substance decreases on expanding according to the relation ρ2=ρ11+γ(T2−T1), where , ρ1→density atT1,ρ2→density atT2,γ→ coefficient of volume expansion of substances. When a solid is submerged in a liquid , liquid exerts an upward force on solid which is equal to the weight of liquid displaced by submerged part of solid. Solid will float or sink depends on relative densities of solid and liquid . A cubical block of solid floats in a liquid with half ot its volume submerged in liquid as shown in figure (at temperature T) αS→ Coefficient of linear expansion of solid
γL→Coefficient of volume expansion of liquid
ρS→Density of solid at temperatureT
ρL→ Density of liquid at temperatureT
_E01_197_Q01.png)
The relation between densities of solid and liquid at temperature T is
View SolutionSolids and liquids both expands on heating. The density of substance decreases on expanding according to the relation ρ2=ρ11+γ(T2−T1), where , ρ1→density atT1,ρ2→density atT2,γ→ coefficient of volume expansion of substances. When a solid is submerged in a liquid , liquid exerts an upward force on solid which is equal to the weight of liquid displaced by submerged part of solid. Solid will float or sink depends on relative densities of solid and liquid . A cubical block of solid floats in a liquid with half ot its volume submerged in liquid as shown in figure (at temperature T) αS→ Coefficient of linear expansion of solid
γL→Coefficient of volume expansion of liquid
ρS→Density of solid at temperatureT
ρL→ Density of liquid at temperatureT
_E01_198_Q01.png)
If temperature of system increases, then fraction of solid submerged in liquid
View SolutionSolids and liquids both expands on heating. The density of substance decreases on expanding according to the relation ρ2=ρ11+γ(T2−T1), where , ρ1→density atT1,ρ2→density atT2,γ→ coefficient of volume expansion of substances. When a solid is submerged in a liquid , liquid exerts an upward force on solid which is equal to the weight of liquid displaced by submerged part of solid. Solid will float or sink depends on relative densities of solid and liquid . A cubical block of solid floats in a liquid with half ot its volume submerged in liquid as shown in figure (at temperature T) αS→ Coefficient of linear expansion of solid
γL→Coefficient of volume expansion of liquid
ρS→Density of solid at temperatureT
ρL→ Density of liquid at temperatureT
_E01_200_Q01.png)
Imagine the depth of the block submerged in the liquid ,does not change on increasing temperature then
View SolutionSolids and liquids both expands on heating. The density of substance decreases on expanding according to the relation ρ2=ρ11+γ(T2−T1), where , ρ1→density atT1,ρ2→density atT2,γ→ coefficient of volume expansion of substances. When a solid is submerged in a liquid , liquid exerts an upward force on solid which is equal to the weight of liquid displaced by submerged part of solid. Solid will float or sink depends on relative densities of solid and liquid . A cubical block of solid floats in a liquid with half ot its volume submerged in liquid as shown in figure (at temperature T) αS→ Coefficient of linear expansion of solid
γL→Coefficient of volume expansion of liquid
ρS→Density of solid at temperatureT
ρL→ Density of liquid at temperatureT
_E01_199_Q01.png)
Imagine fraction submerged does not change on increasing temperature the relation between γL and αS is
View Solution
