A sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P3.
Which of the following is correct?
P1V1=P2V2
P1/P2=V1/V2
P1/P2=P1/P3
P1=P2
To analyze the problem of an ideal gas undergoing isothermal and adiabatic expansions, let's break down the steps involved in deriving the relationships between the pressures and volumes at different states.
1. Understanding Isothermal Expansion:
- In an isothermal process, the temperature remains constant. For an ideal gas, we can use the ideal gas law, which states:
PV=nRT
- For the initial state (1) and final state (2) during isothermal expansion, we have:
P1V1=P2V2
- This equation indicates that the product of pressure and volume remains constant during the isothermal process.
2. Understanding Adiabatic Expansion:
- In an adiabatic process, there is no heat exchange with the surroundings. For an ideal gas undergoing adiabatic expansion, we can use the following relation:
PVγ=constant
- Here, γ (gamma) is the heat capacity ratio (C_p/C_v).
- For the initial state (1) and final state (3) during adiabatic expansion, we have:
P1Vγ1=P3Vγ2
- Rearranging this gives us:
P1Vγ1=P3Vγ2⟹P1=P3(V1V2)γ
3. Relating Pressures:
- From the isothermal process, we can express V2 in terms of V1 and pressures:
V2=P1P2V1
- Substituting this into the adiabatic equation gives:
P1=P3⎛⎜⎝V1P1P2V1⎞⎟⎠γ=P3(P2P1)γ
4. Final Relationships:
- Rearranging the above equation leads to:
P1P3=(P2P1)γ
- This shows that the ratio of pressures during the adiabatic process is related to the pressures during the isothermal process, scaled by the factor of γ.
5. Conclusion:
- From the analysis, we can conclude that:
- The pressure after isothermal expansion P2 is greater than the pressure after adiabatic expansion P3 (i.e., P3<P2).
- The correct statement is that P1V1=P2V2 holds true for the isothermal process.
- In an isothermal process, the temperature remains constant. For an ideal gas, we can use the ideal gas law, which states:
PV=nRT
- For the initial state (1) and final state (2) during isothermal expansion, we have:
P1V1=P2V2
- This equation indicates that the product of pressure and volume remains constant during the isothermal process.
- In an adiabatic process, there is no heat exchange with the surroundings. For an ideal gas undergoing adiabatic expansion, we can use the following relation:
PVγ=constant
- Here, γ (gamma) is the heat capacity ratio (C_p/C_v).
- For the initial state (1) and final state (3) during adiabatic expansion, we have:
P1Vγ1=P3Vγ2
- Rearranging this gives us:
P1Vγ1=P3Vγ2⟹P1=P3(V1V2)γ
- From the isothermal process, we can express V2 in terms of V1 and pressures:
V2=P1P2V1
- Substituting this into the adiabatic equation gives:
P1=P3⎛⎜⎝V1P1P2V1⎞⎟⎠γ=P3(P2P1)γ
- Rearranging the above equation leads to:
P1P3=(P2P1)γ
- This shows that the ratio of pressures during the adiabatic process is related to the pressures during the isothermal process, scaled by the factor of γ.
- From the analysis, we can conclude that:
- The pressure after isothermal expansion P2 is greater than the pressure after adiabatic expansion P3 (i.e., P3<P2).
- The correct statement is that P1V1=P2V2 holds true for the isothermal process.
Topper's Solved these Questions
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Exercises (Multiple Correct)50videos
THERMODYNAMICS
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Multiple correct Answer Type2videos
THERMODYNAMICS
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Paragraph for Problem1videos
THERMODYNAMICS
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STOICHIOMETRYEXERCISE - Archives Subjective33videos
STOICHIOMETRY
Similar Questions
A sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P3.
Which relation is correct (γ=CPCV)?View SolutionA sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P2.
Which graphic representation is correct
a.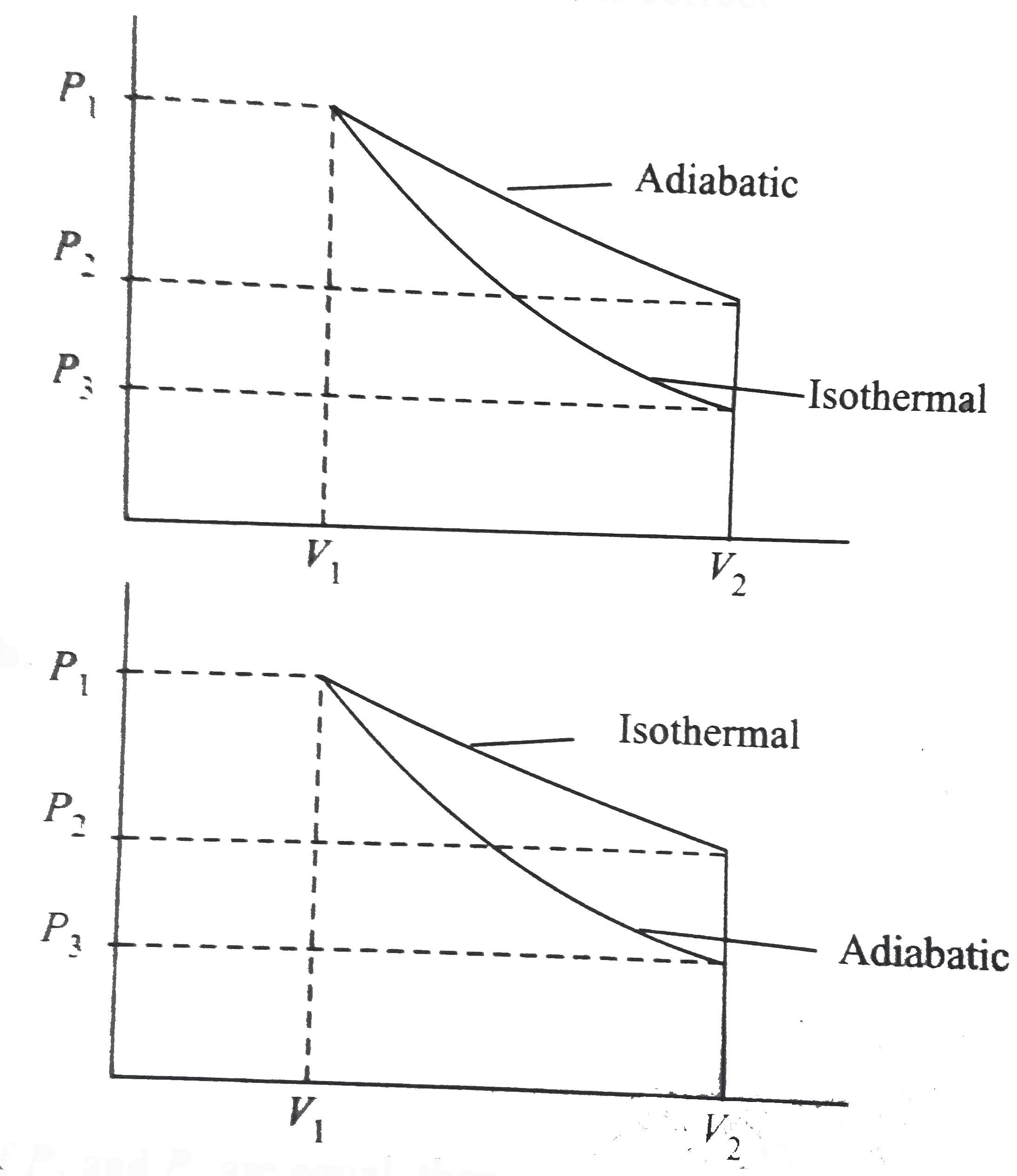 View Solution
View SolutionA sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P3.
The work of expansion in adiabatic process (wadi) is related to work of expansion in isothermal process (wiso) isView SolutionA sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P2.
If P3 and P2 are equal, thenView SolutionAn ideal gas expands isothermally from volume V1 to V2 and is then compressed to original volume V1 adiabatically. Initialy pressure is P1 and final pressure is P3. The total work done is W. Then
View SolutionAn ideal gas expands isothermally from volume V1 to V2 and is then compressed to original volume V1 adiabatically. Initialy pressure is P1 and final pressure is P3. The total work done is W. Then
View Solution1mol of an ideal gas undergoes reversible isothermal expansion form an initial volume V1 to a final volume 10V1 and does 10kJ of work. The initial pressure was 1×107Pa.
c. Calculate V2.
b. If there were 2mol of gas, what must its temperature have been?View Solution1mol of an ideal gas undergoes reversible isothermal expansion form an initial volume V1 to a final volume 10V1 and does 10kJ of work. The initial pressure was 1×107Pa.
a. Calculate V2.
b. If there were 2mol of gas, what must its temperature have been?View SolutionAn ideal gas undergoes isothermal expansion followed by heat removel at constant volume and they by heat removal at constant pressure to the initial volume. The correct descripion of these steps is indicated by
View SolutionA sample of gas expands from volume V1 to V2. The amount of work done by the gas is greatest when the expansion is
View Solution

