A reaction attains equilibrium state under standard conditions, then:
Equilibrium constant K=0
Equilibrium constant K=1
ΔGΘ=0 and ΔHΘ=TΔSΘ
ΔG=0 and ΔH=TΔS
To solve the question regarding the equilibrium state of a reaction under standard conditions, we can follow these steps:
1. Understanding the Gibbs Free Energy Equation:
The Gibbs free energy change (ΔG) for a reaction can be expressed as:
ΔG=ΔG∘+2.303RTlogQc
where:
- ΔG is the Gibbs free energy change at any point.
- ΔG° is the standard Gibbs free energy change.
- R is the universal gas constant.
- T is the temperature in Kelvin.
- Q_c is the reaction quotient.
2. Setting Conditions at Equilibrium:
At equilibrium, the Gibbs free energy change (ΔG) is equal to zero:
ΔG=0
Therefore, we can set the equation to:
0=ΔG∘+2.303RTlogQc
3. Standard Conditions:
The problem states that the reaction attains equilibrium under standard conditions. Under standard conditions, ΔG° is also equal to zero:
ΔG∘=0
4. Substituting Values:
Substituting ΔG° = 0 into the equation gives:
0=0+2.303RTlogQc
This simplifies to:
2.303RTlogQc=0
5. Solving for Q_c:
Since 2.303RT is not zero (as R and T are positive constants), we can conclude that:
logQc=0
This implies:
Qc=100=1
At equilibrium, the equilibrium constant Kc is equal to Q_c, thus:
Kc=1
6. Relating ΔG° to ΔH° and ΔS°:
We also know from thermodynamics that:
ΔG∘=ΔH∘−TΔS∘
Since ΔG° = 0, we can write:
0=ΔH∘−TΔS∘
Rearranging gives:
ΔH∘=TΔS∘
Conclusion:
From the above steps, we conclude that:
- Kc=1
- ΔG∘=0
- ΔH∘=TΔS∘
The Gibbs free energy change (ΔG) for a reaction can be expressed as:
ΔG=ΔG∘+2.303RTlogQc
where:
- ΔG is the Gibbs free energy change at any point.
- ΔG° is the standard Gibbs free energy change.
- R is the universal gas constant.
- T is the temperature in Kelvin.
- Q_c is the reaction quotient.
At equilibrium, the Gibbs free energy change (ΔG) is equal to zero:
ΔG=0
Therefore, we can set the equation to:
0=ΔG∘+2.303RTlogQc
The problem states that the reaction attains equilibrium under standard conditions. Under standard conditions, ΔG° is also equal to zero:
ΔG∘=0
Substituting ΔG° = 0 into the equation gives:
0=0+2.303RTlogQc
This simplifies to:
2.303RTlogQc=0
Since 2.303RT is not zero (as R and T are positive constants), we can conclude that:
logQc=0
This implies:
Qc=100=1
At equilibrium, the equilibrium constant Kc is equal to Q_c, thus:
Kc=1
We also know from thermodynamics that:
ΔG∘=ΔH∘−TΔS∘
Since ΔG° = 0, we can write:
0=ΔH∘−TΔS∘
Rearranging gives:
ΔH∘=TΔS∘
From the above steps, we conclude that:
- Kc=1
- ΔG∘=0
- ΔH∘=TΔS∘
Topper's Solved these Questions
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Multiple correct Answer Type
2 Videos
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Exercises (Single Correct)
62 Videos
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Exercises (Linked Comprehension)
74 Videos
- STOICHIOMETRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STOICHIOMETRYEXERCISE - Archives Subjective
33 Videos
Similar Questions
A reaction attains equilibrium, when the free energy change is
View SolutionVan't Hoff's equation for a chemical reaction under equilibrium is given by standard reaction enthalpy at temperature T and K is the equilibrium constant . Predict how K will vary with temperature for an exothermic
View Solution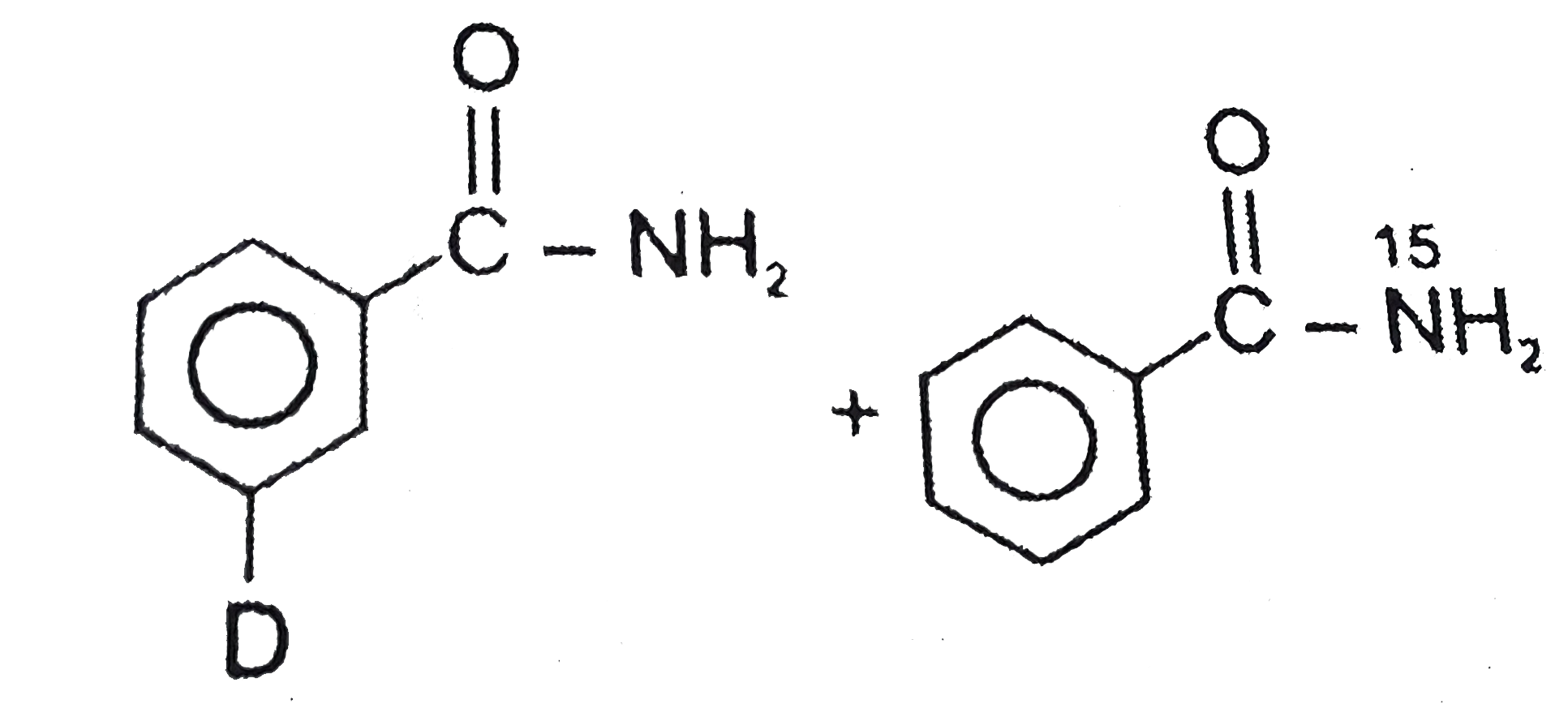 under Hofmann conditions will give:
under Hofmann conditions will give:
View SolutionFor a system in equilibrium, ΔG=0, under conditions of constant
View SolutionThe number of moles of oxygen in 1 L of air containing 21% oxygen by volume , under standard conditions , is
View SolutionThe number of moles of nitrogen present in one litre of air containing 14% nitrogen by volume, under standard condition, is:
View SolutionThe number of moles of nitrogen present in one litre of air containing 13% nitrogen by volume, under standard condition, is:
View SolutionThe number of moles of nitrogen present in one litre of air containing 20% nitrogen by volume, under standard condition, is:
View SolutionThe number of moles of nitrogen present in one litre of air containing 12% nitrogen by volume, under standard condition, is:
View SolutionThe number of moles of nitrogen present in one litre of air containing 15% nitrogen by volume, under standard condition, is:
View Solution
