When α−D glucose is dissolved in water, it undergoes a partial converion to β−D glucose to exhibit mutarotation. This conversion stops when 63.6% of glucose is in β form. Assuming that equilibrium has been attained, calculate Kc for mutarotation.
To calculate the equilibrium constant Kc for the mutarotation of α−D glucose to β−D glucose, we can follow these steps:
Step 1: Understand the Reaction
The mutarotation of glucose can be represented as:
α−D glucose⇌β−D glucose
Step 2: Define Initial Conditions
Initially, when α−D glucose is dissolved in water, we have:
- Concentration of α−D glucose = 1 mole (let's assume 1 mole for simplicity)
- Concentration of β−D glucose = 0 moles
Step 3: Define the Change at Equilibrium
At equilibrium, it is given that 63.6% of the glucose is in the β form. This means:
- Concentration of β−D glucose = 0.636 moles
- Concentration of α−D glucose = 1−0.636=0.364 moles
Step 4: Write the Expression for Kc
The expression for the equilibrium constant Kc for the reaction is:
Kc=(β−D glucose)(α−D glucose)
Step 5: Substitute the Values into the Kc Expression
Substituting the equilibrium concentrations into the expression gives:
Kc=0.6360.364
Step 6: Calculate Kc
Now, performing the calculation:
Kc=0.6360.364≈1.747
Final Answer
Thus, the equilibrium constant Kc for the mutarotation of glucose is approximately:
Kc≈1.747
---
The mutarotation of glucose can be represented as:
α−D glucose⇌β−D glucose
Initially, when α−D glucose is dissolved in water, we have:
- Concentration of α−D glucose = 1 mole (let's assume 1 mole for simplicity)
- Concentration of β−D glucose = 0 moles
At equilibrium, it is given that 63.6% of the glucose is in the β form. This means:
- Concentration of β−D glucose = 0.636 moles
- Concentration of α−D glucose = 1−0.636=0.364 moles
The expression for the equilibrium constant Kc for the reaction is:
Kc=(β−D glucose)(α−D glucose)
Substituting the equilibrium concentrations into the expression gives:
Kc=0.6360.364
Now, performing the calculation:
Kc=0.6360.364≈1.747
Thus, the equilibrium constant Kc for the mutarotation of glucose is approximately:
Kc≈1.747
Topper's Solved these Questions
- CHEMICAL EQUILIBRIUMBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Concept Applicationexercise 7.1
53 Videos
- CHEMICAL EQUILIBRIUMBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Ex 7.2
40 Videos
- CHEMICAL BONDING AND MOLECULAR STRUCTUREBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL BONDING AND MOLECULAR STRUCTUREEXERCISE - Archives Subjective
15 Videos
- CLASSIFICATION AND NOMENCLATURE OF ORGANIC COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CLASSIFICATION AND NOMENCLATURE OF ORGANIC COMPOUNDSEXERCISE - Analytical and Descriptive Type
3 Videos
Similar Questions
During mutarotation of β-D-glucose in aqueous solution angle of optical rotation
View SolutionWhen either form of D-Glucose is dissolved In water, the solution gradually changes its optical rotation and finally attains a constant optical rotation of +52∘.

Which form of D-GIucose is more stable?
View Solution
Knowledge Check
D (+) Glucose has melting point 146∘C and specific rotation [α]25D is + 112∘C. Another D(+) Glucose has melting point 150∘C and specific rotational [α]25Dis +18.7∘C. The two form have significantly different optical rotation but when an aqueous solution of either form is allowed to stand, it rotation changes. The specific rotation of one form decreases and rotation of other increases until both solution show the same value +52.7∘. The change in rotation towards an equilibrium value is called mutarotation.
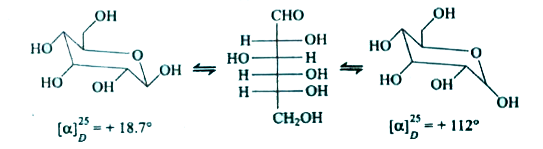
What percentage of β-D-(+) glucopyranose found at equilibrium in the aqueous solution?A50%B≈100%C38%D64%D (+) Glucose has melting point 146∘C and specific rotation [α]25D is + 112∘C. Another D(+) Glucose has melting point 150∘C and specific rotational [α]25Dis +18.7∘C. The two form have significantly different optical rotation but when an aqueous solution of either form is allowed to stand, it rotation changes. The specific rotation of one form decreases and rotation of other increases until both solution show the same value +52.7∘. The change in rotation towards an equilibrium value is called mutarotation.
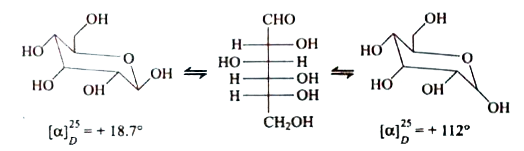
Mutarotation is characteristic feature of:AEpimerBEnantiomerCAnomerDRing chain isomerD (+) Glucose has melting point 146∘C and specific rotation [α]25D is + 112∘C. Another D(+) Glucose has melting point 150∘C and specific rotational [α]25Dis +18.7∘C. The two form have significantly different optical rotation but when an aqueous solution of either form is allowed to stand, it rotation changes. The specific rotation of one form decreases and rotation of other increases until both solution show the same value +52.7∘. The change in rotation towards an equilibrium value is called mutarotation.
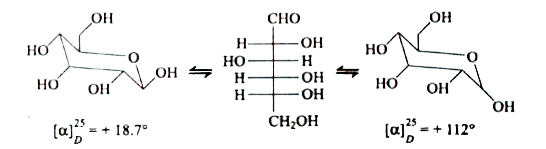
For mannose the mutarotation can be shown in brief as follow:
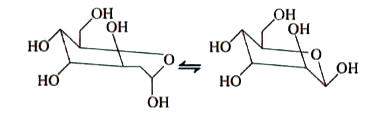 Aα-formBβ-formCopen chainDNone of these
Aα-formBβ-formCopen chainDNone of these
A sugar exist in two isomeric form α−D & β−D with specific rotation of 110∘ and 30∘ respectively. When α−D form of the suar is dissolved in water exhibits mutarotation till the equilibrium value of 90∘ is attained. The equilibrium constant of mutarotation of β−D form [Assuming only α and β form in solution] is equal to:
View SolutionWhen either form of D-Glucose is dissolved In water, the solution gradually changes its optical rotation and finally attains a constant optical rotation of +52∘.

Which of the following statements, is true?
View SolutionWhen either form of D-Glucose is dissolved In water, the solution gradually changes its optical rotation and finally attains a constant optical rotation of +52∘.

What is the percentage of open chain D-Glucose in solution?
View Solutionα−(D) glucose ⇔β−(D) glucose, equilibrium constant for this s 1.8. The percentage of α−(D) glucose at equilibrium is
View SolutionWhen (+) sucrose is hydrolysed, the D-glucose mutarotates downward to +52.7∘. What does this indicate about the structures of (+)-sucrose?
View Solution
