Mass action rato or reaction quotient Q for a reaction can be calculate using the law of masss action
A(g)+B(g)⇔C(g)+D(g)
Q=[C][D][A][B]
The value of Q decides whether the reaction is at equilibrium or not.
At equilibrium, Q=K
For an equilibrium process, Q≠K
when Q>K, reaction will favour backward direction and when Q<K, it will favour direction.
Answer the following questions:
For the reaction:
2A+B⇔3C at 298K,Kc=40
A 4L vessel contains 2,1, and 4 mol of A, B and c, respectively. The reaction at the same temperature
Must proceed in forward direction
Must proceed in backward direction
Must be in equilibrium
Cannot be predicted
The correct Answer is:A
To solve the problem step by step, we will follow these instructions:
Step 1: Write the balanced chemical equation and identify the equilibrium constant expression.
The given reaction is:
2A+B⇌3C
The equilibrium constant expression Kc for this reaction is given by:
Kc=(C)3(A)2(B)
Step 2: Calculate the concentrations of the reactants and products.
We are given the number of moles of A, B, and C in a 4 L vessel:
- Moles of A = 2
- Moles of B = 1
- Moles of C = 4
To find the concentrations, we use the formula:
Concentration=Number of molesVolume in liters
Calculating the concentrations:
- Concentration of A:
(A)=2 moles4 L=0.5M
- Concentration of B:
(B)=1 mole4 L=0.25M
- Concentration of C:
(C)=4 moles4 L=1M
Step 3: Calculate the reaction quotient Q.
Using the concentrations calculated, we can now find Q:
Q=(C)3(A)2(B)
Substituting the values:
Q=(1)3(0.5)2(0.25)
Calculating:
Q=10.25×0.25=10.0625=16
Step 4: Compare Q with Kc.
Given that Kc=40:
- Since Q=16 and Kc=40, we have:
Q<Kc
Step 5: Determine the direction of the reaction.
Since Q<Kc, the reaction will favor the forward direction to reach equilibrium.
Final Conclusion:
The reaction will proceed in the forward direction because the reaction quotient Q is less than the equilibrium constant Kc.
---
The given reaction is:
2A+B⇌3C
Kc=(C)3(A)2(B)
We are given the number of moles of A, B, and C in a 4 L vessel:
- Moles of A = 2
- Moles of B = 1
- Moles of C = 4
Concentration=Number of molesVolume in liters
- Concentration of A:
(A)=2 moles4 L=0.5M
- Concentration of B:
(B)=1 mole4 L=0.25M
- Concentration of C:
(C)=4 moles4 L=1M
Using the concentrations calculated, we can now find Q:
Q=(C)3(A)2(B)
Q=(1)3(0.5)2(0.25)
Q=10.25×0.25=10.0625=16
Given that Kc=40:
- Since Q=16 and Kc=40, we have:
Q<Kc
Since Q<Kc, the reaction will favor the forward direction to reach equilibrium.
The reaction will proceed in the forward direction because the reaction quotient Q is less than the equilibrium constant Kc.
Topper's Solved these Questions
- CHEMICAL EQUILIBRIUMBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Exercises (Multiple Correct)
26 Videos
- CHEMICAL EQUILIBRIUMBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Exercises (Single Correct)
58 Videos
- CHEMICAL EQUILIBRIUMBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Exercises (Subjective)
46 Videos
- CHEMICAL BONDING AND MOLECULAR STRUCTUREBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL BONDING AND MOLECULAR STRUCTUREEXERCISE - Archives Subjective
15 Videos
- CLASSIFICATION AND NOMENCLATURE OF ORGANIC COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CLASSIFICATION AND NOMENCLATURE OF ORGANIC COMPOUNDSEXERCISE - Analytical and Descriptive Type
3 Videos
Similar Questions
Mass action rato or reaction quotient Q for a reaction can be calculate using the law of masss action
A(g)+B(g)⇔C(g)+D(g)
Q=[C][D][A][B]
The value of Q decides whether the reaction is at equilibrium or not.
At equilibrium, Q=K
For an equilibrium process, Q≠K
when Q>K, reaction will favour backward direction and when Q<K, it will favour direction.
Answer the following questions:
In the reaction:
NH4Cl(g)⇔NH3(g)+HCl(g)
a graph is plotted to show that the variation or the rate of forward and backward reaction against time.
Which of following is correct?
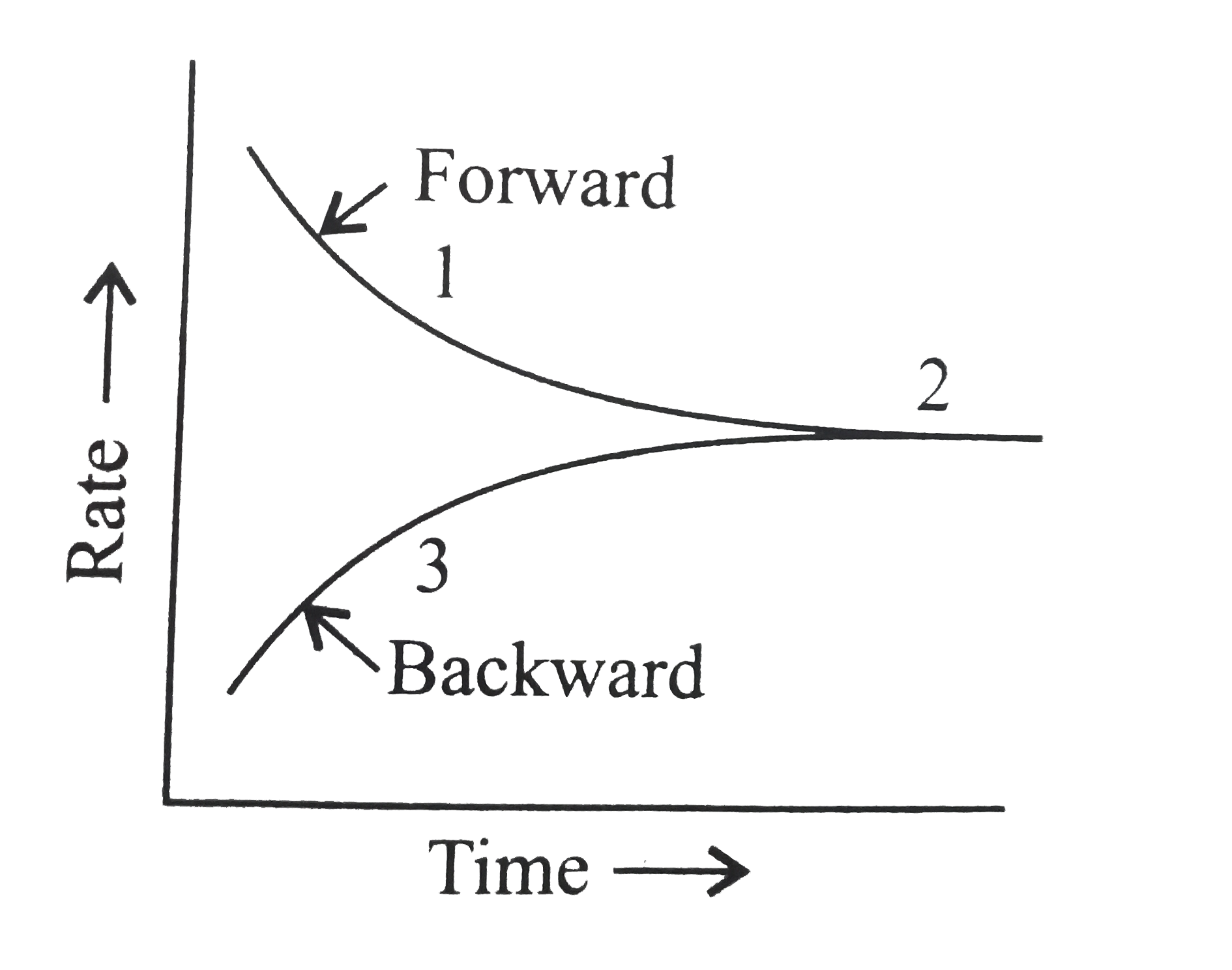
View SolutionMass action rato or reaction quotient Q for a reaction can be calculate using the law of masss action
A(g)+B(g)⇔C(g)+D(g)
Q=[C][D][A][B]
The value of Q decides whether the reaction is at equilibrium or not.
At equilibrium, Q=K
For an equilibrium process, Q≠K
when Q>K, reaction will favour backward direction and when Q<K, it will favour direction.
Answer the following questions:
In the following reaction:
2SO2(g)+O2(g)⇔2SO3(g)
the equilibrium is not attained. The rate of forward reaction is greater than that of backward reaction. Thus, which of the following is the correct relation between Kp and Qp?
View SolutionMass action rato or reaction quotient Q for a reaction can be calculate using the law of masss action
A(g)+B(g)⇔C(g)+D(g)
Q=[C][D][A][B]
The value of Q decides whether the reaction is at equilibrium or not.
At equilibrium, Q=K
For an equilibrium process, Q≠K
when Q>K, reaction will favour backward direction and when Q<K, it will favour forward direction.
Answer the following questions:
In a reaction mixture containing H2,N2 and NH3 at partial pressure of 2 atm, 1 atm and 3 atm respectively, the value of Kp at 700K is 4.00×10−5atm−2. In which direction the net reaction will go?
N2(g)+3H2(g)⇔2NH3(g)
View SolutionMass action rato or reaction quotient Q for a reaction can be calculate using the law of masss action
A(g)+B(g)⇔C(g)+D(g)
Q=[C][D][A][B]
The value of Q decides whether the reaction is at equilibrium or not.
At equilibrium, Q=K
For an equilibrium process, Q≠K
when Q>K, reaction will favour backward direction and when Q<K, it will favour direction.
Answer the following questions:
The reaction quotient Q for:
O2(g)+2H2(g)⇔2H2O(g)
is given by Q=[H2O]2[O2][H2]2. The reaction will proceed in backward direction, when
View SolutionThe relation between KPandKC for the reaction A(g)+B(g)⇔C(g)+2D(g) is -
View SolutionThe Kc for given reaction will be A2(g)+2B(g)⇔C(g)+2D(s)
View SolutionThe unit of equilibrium constant Kc for the reaction A+B⇔C would be
View SolutionThe reaction Quotient (Q) predicts:
View SolutionThe gaseous reaction A(g)+B(g)⇔2C(g)+D(g)+q kJ is most favoured at :
View SolutionTwo moles of each reactant A and B are taken in a reaction flask. They react in the following manner,
A(g)+B(g)⇔C(g)+D(g)
At equilibrium, it was found that the concentration of C is triple to that of B the equilibrium constant for the reaction is
View Solution
