A compound made of particles A and B. A forms fcc packing and B occupies all the OVs. If all the particles along the plane as shown in the figure below are removeed, then the simplest formula of the compound is

A5B7
A7B5
AB
AB3.75
The correct Answer is:C
c. Since the lattice is fcc(Zeff=4), therefore, numbered of A ions =4(1 corner +3 face centre)
(OVs are formed at body centre andedge centre). ltbr> Lons are removed from the plane (PQRS) as shown in the figure. From the figure, it is clear, 4 corner ions and two edge centre ions on PQ and RS are alos removed.
Also two face centre ions lying on PR and QS along with one ions on present in the body centre are removed as shown in the figure below.
b
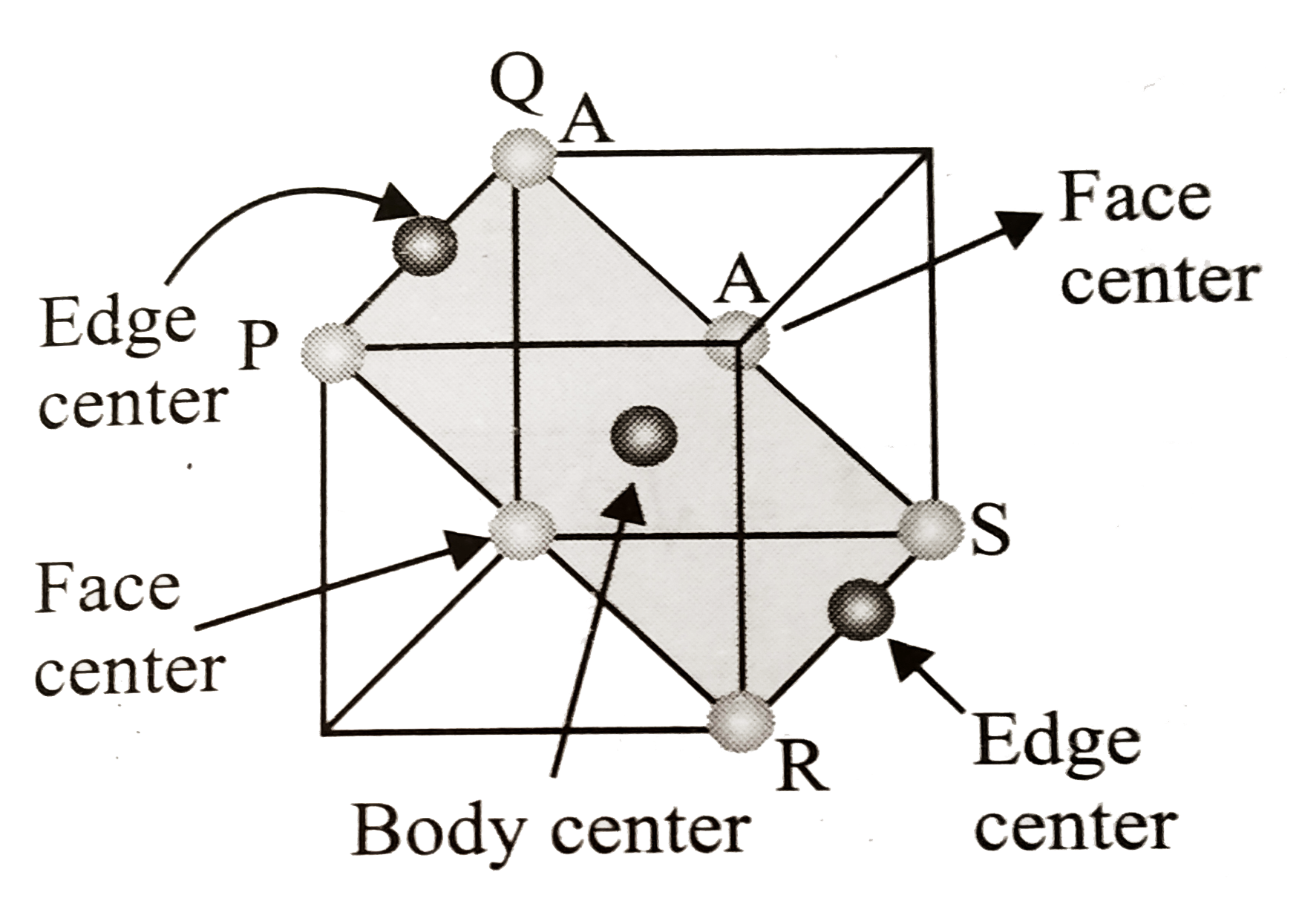
∴ Number of A ions removed
=4×18 (corner share) +2×12 (face centre share)
=12+1=112
Number of B ions removed
2×14 (edge centre share) +11 (body centre share)
=12+1=112
Number of A ions left =4−112=2.5
Number of B ions left =4−112=2.5
Thus, formula =A2.5B2.5=2.5AB
Simplest formula =AB
Topper's Solved these Questions
- SOLID STATEBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLID STATEEXERCISE - Solved Examples
13 Videos
- SOLID STATEBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLID STATEEXERCISE - Exercises (Linked Comprehension)
13 Videos
- REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSEXERCISE - SUBJECTIVE TYPE
4 Videos
- SOLUTIONSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLUTIONSEXERCISE - Ex 2.3 (Objective)
9 Videos
Similar Questions
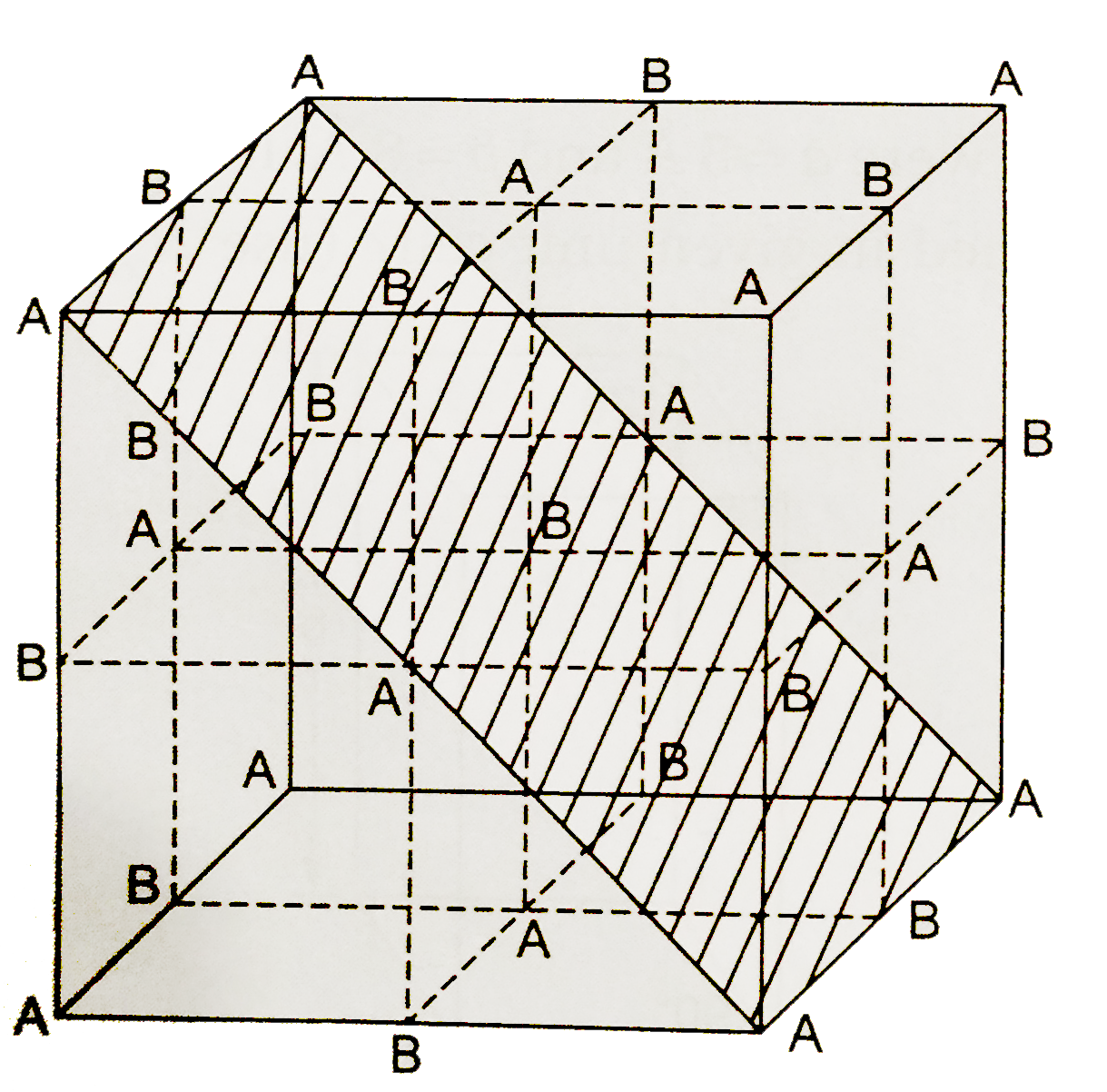
A crystal is made of particles A and B . From fcc packing and B occupies all the octahedral voids . If all the particle along the plane as shown in figure are removed , then, the formula of the crystal would be :
View SolutionA crystal is made of particles X and Y.X form fcc packing and Y occupies all the octahedral voids . If all the particles along one body diagonal are removed then the formula of the crystal would de :
View SolutionA compound made of particles A, B, and C forms p lattice. Ions A are at lattice points, B occupy TVsC occupy OVs. If all the ions along one of the edge axis are removed, then formula of the compound is
View SolutionA crystal is made of particles X,Y and Z.X form fcc packing . Y occupies all the octahedral void of X and Z occupies all the tetrahedral voids of X . If all the particles along one body diagonal are removed then the formula of the crystal would be:
View SolutionA crystal is made of particles X,Y and Z.X form fcc packing . Y occupies all the octahedral void of X and Z occupies all the tetrahedral voids of X . If all the particles along one body diagonal are removed then the formula of the crystal would be:
View SolutionIn a crystalline solid, atoms of X form fcc packing and atoms of Y occupy all octahedral voids. If all the atoms along one body diagonal are removed, what is the simplest formula of the crystalline lattice solid?
View SolutionA compound made of particles A, B, and C forms p lattice. In the lattice, ions A occupy the lattice points and ions B and C occuphy the alternate TVs. If all the ions along one of the body diagonals are removed, then formula of the compound is
View SolutionA2B has antifluorite structure (B forms FCC lattice and A occupies tetrahedral voids).If all ions along any one body diagonal are removed, then new formula of compound will be :
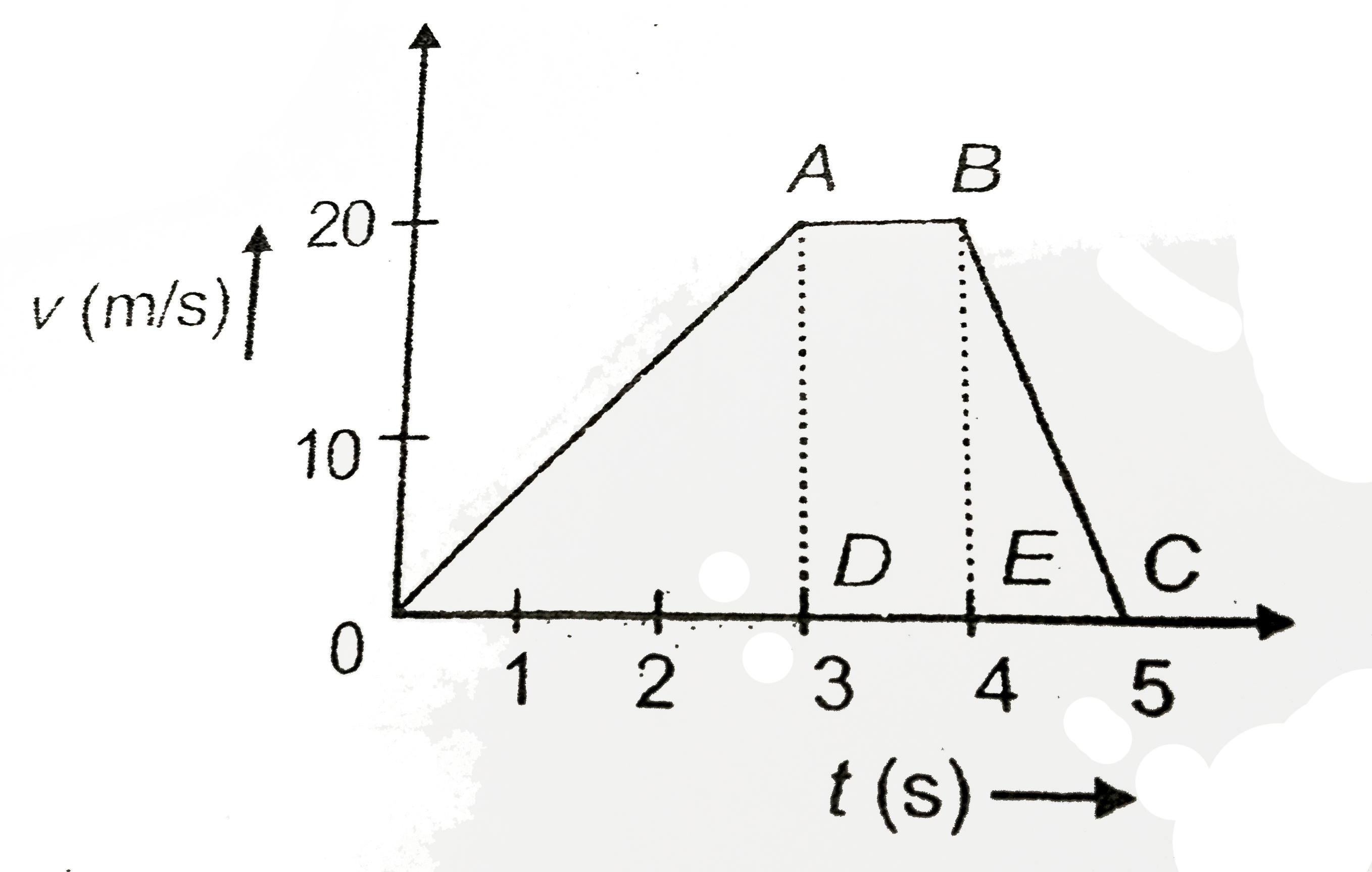
View SolutionThe variation of velocity of a particle moving along a straight line is as shown in the figure given below. The distance travelled by the particle in 5 s is
View SolutionIn a solid AB, A atoms have a ccp arrangement and B atoms occupy all the octahedral sites. If all the face-centred atoms along one of the axes passing through body centres are removed, then what will be the resultant stoichiometry of compound ?
View Solution
