The molar volumes of and are and , respectively. Find the ratio of the unit cube edges of the two crystals. Assume both have the same packing efficiency.
To find the ratio of the unit cube edges of KCl and NaCl, we can follow these steps:
Step 1: Understand the relationship between molar volume and unit cell edge length
The molar volume (V_m) of a substance is related to the volume of its unit cell (V_cell) and the number of formula units per unit cell (Z). The formula is given by:
Vm=VcellZ
For both KCl and NaCl, we know that they have a face-centered cubic (FCC) structure, which means Z = 4 for both.
Step 2: Calculate the volume of the unit cell for KCl and NaCl
Given the molar volumes:
- For KCl, V_m(KCl) = 40 mL
- For NaCl, V_m(NaCl) = 30 mL
Using the relationship:
Vcell=Vm×Z
We can calculate the volume of the unit cell for both salts:
Vcell(KCl)=40mL×4=160mL
Vcell(NaCl)=30mL×4=120mL
Step 3: Relate the volume of the unit cell to the edge length
The volume of the unit cell is also related to the edge length (a) of the cube:
Vcell=a3
Step 4: Set up the ratio of the unit cell volumes
Now we can set up the ratio of the volumes of the unit cells:
Vcell(KCl)Vcell(NaCl)=160120=43
Step 5: Find the ratio of the edge lengths
Taking the cube root of the ratio of the volumes gives us the ratio of the edge lengths:
aKClaNaCl=(Vcell(KCl)Vcell(NaCl))1/3=(43)1/3
Calculating this gives:
aKClaNaCl=41/331/3≈1.5871.442≈1.1
Final Answer
Thus, the ratio of the unit cube edges of KCl to NaCl is approximately:
aKClaNaCl≈1.113
The molar volume (V_m) of a substance is related to the volume of its unit cell (V_cell) and the number of formula units per unit cell (Z). The formula is given by:
Given the molar volumes:
- For KCl, V_m(KCl) = 40 mL
- For NaCl, V_m(NaCl) = 30 mL
Vcell(NaCl)=30mL×4=120mL
The volume of the unit cell is also related to the edge length (a) of the cube:
Now we can set up the ratio of the volumes of the unit cells:
Taking the cube root of the ratio of the volumes gives us the ratio of the edge lengths:
Thus, the ratio of the unit cube edges of KCl to NaCl is approximately:
Topper's Solved these Questions
- SOLID STATEBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLID STATEEXERCISE - Exercises (Linked Comprehension)
13 Videos
- SOLID STATEBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLID STATEEXERCISE - Exercises (Multiple Correct)
39 Videos
- SOLID STATEBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLID STATEEXERCISE - Ex 1.2 (Objective)
9 Videos
- REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSEXERCISE - SUBJECTIVE TYPE
4 Videos
- SOLUTIONSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLUTIONSEXERCISE - Ex 2.3 (Objective)
9 Videos
Similar Questions
The molar volume of KCl and NaCl are 37.46 mL and 27.94mL respectively . The ratio of the unit cube edges of the two crystals is
View SolutionSuppose that there are two cubes, having edges 2cm and 4cm, respectively. Find the volumes V1and V2 of the cubes and compare them.
View SolutionTwo vessel having equal volume contain molecular hydrogen at one atmosphere and helium at two atmospheres respectively. What is the ratio of rms speed of hydrogen molecule to that of helium molecule? ( Assume both the samples are at same temperature)
View SolutionThe two ions A+ and B− have radii 40 pm and 120 pm respectively. In the closed packed crystal of compound AB, the coordination number of A+ would be
View SolutionTwo objects of massses m1 and m2 having the same size are dropped simultaneously from hights h1andh2 respectively. Find out the ratio of time they would take in reaching the ground. Will this ratio remain the same if (i)one of the objects is hollow and the other one is solid and (ii)both of them are hollow, size remaining the same in each case. give reason.
View SolutionTwo inflated ballons I and II (thin skin) having volume 600 mL and 1500 mL at 300 K are taken as shown in diagram. If maximum volume of inner and outer balloons are 800 mL and 1800 mL respectively then find the balloon which will burst first on gradual heating.
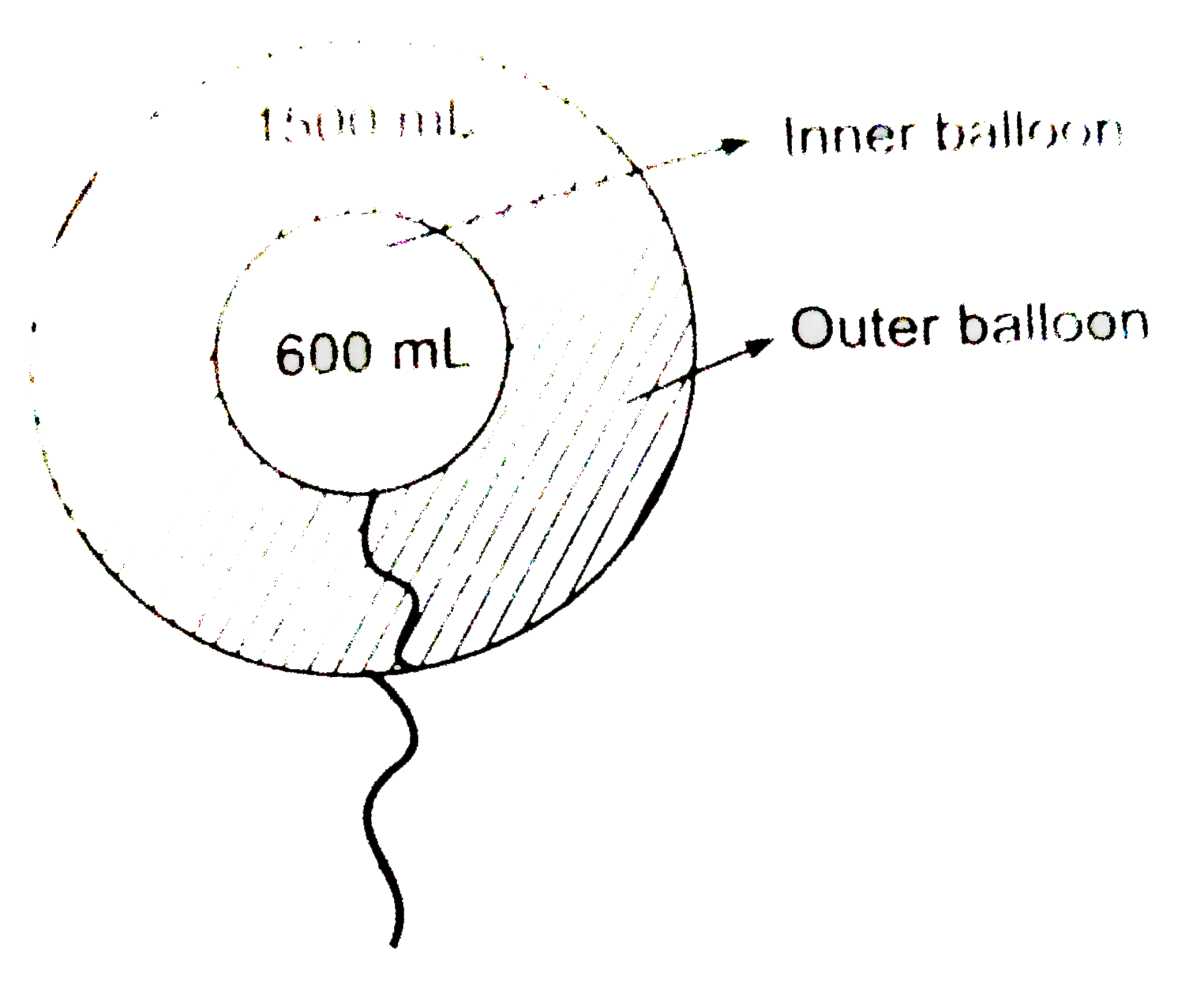
View SolutionTwo cubes have their volumes in the ratio 1 : 27. Find the ratio of their surface areas.
View SolutionTwo wires of the same material and having the same uniform area of cross section are connected in an electric circuit. The masses of the wires are mand2m, respectively. When a current I flows through both of them connected in series, then find the ratio of heat produced in them in a given time .
View SolutionCubes A, B, C having edges 18cm, 24cm and 30cm respectively are melted and moulded into a new cube D. Find the edge of the bigger cube D.
View SolutionTwo toroids 1 and 2 have total number of turns 200 and 100 respectively with average radii 40cm and 20cm respectively. If they carry same current i, the ratio of the magnetic fields along the two loops is
(a) 1:1
(b) 4:1
(c) 2:1
(d) 1:2
View Solution
