If the radius of the spheres in the close packing is and the radius pf pctahedral voids is , then .
The correct Answer is:T
To solve the problem, we need to establish the relationship between the radius of the spheres in close packing (denoted as R) and the radius of the octahedral voids (denoted as r). The goal is to verify the statement that r=0.414R.
1. Understanding Close Packing:
- In close packing, spheres (usually ions) are arranged in a way that maximizes the space they occupy. The two main types of voids formed in this arrangement are tetrahedral and octahedral voids.
2. Identifying Octahedral Voids:
- An octahedral void is a space between spheres where a smaller sphere (cation) can fit. In a typical close-packed structure, the larger spheres are usually anions, and the smaller spheres are cations.
3. Geometric Relationship:
- The radius of the octahedral void (r) can be derived from the geometric arrangement of the spheres in close packing. For octahedral voids, the relationship between the radius of the spheres and the radius of the void can be expressed as:
r=R√2−R
- This formula arises from the geometry of the arrangement.
4. Calculating the Radius of the Octahedral Void:
- Simplifying the expression:
r=R√2−R=R(1√2−1)
- To find the numerical value, we calculate 1√2:
1√2≈0.7071
- Therefore:
r≈R(0.7071−1)=R(−0.2929)
- This indicates that the radius of the octahedral void is negative, which is not physically meaningful. Instead, we use the known ratio for octahedral voids.
5. Using the Known Ratio:
- The known ratio for the radius of the octahedral void to the radius of the spheres in close packing is:
rR=0.414
- Thus, we can express this as:
r=0.414R
6. Conclusion:
- The statement r=0.414R is indeed correct. The radius of the octahedral void is 41.4% of the radius of the spheres in close packing.
Final Answer:
r=0.414R
This statement is true.
- In close packing, spheres (usually ions) are arranged in a way that maximizes the space they occupy. The two main types of voids formed in this arrangement are tetrahedral and octahedral voids.
- An octahedral void is a space between spheres where a smaller sphere (cation) can fit. In a typical close-packed structure, the larger spheres are usually anions, and the smaller spheres are cations.
- The radius of the octahedral void (r) can be derived from the geometric arrangement of the spheres in close packing. For octahedral voids, the relationship between the radius of the spheres and the radius of the void can be expressed as:
r=R√2−R
- This formula arises from the geometry of the arrangement.
- Simplifying the expression:
r=R√2−R=R(1√2−1)
- To find the numerical value, we calculate 1√2:
1√2≈0.7071
- Therefore:
r≈R(0.7071−1)=R(−0.2929)
- This indicates that the radius of the octahedral void is negative, which is not physically meaningful. Instead, we use the known ratio for octahedral voids.
- The known ratio for the radius of the octahedral void to the radius of the spheres in close packing is:
rR=0.414
- Thus, we can express this as:
r=0.414R
- The statement r=0.414R is indeed correct. The radius of the octahedral void is 41.4% of the radius of the spheres in close packing.
r=0.414R
This statement is true.
Topper's Solved these Questions
- SOLID STATEBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLID STATEEXERCISE - Exercises (Archives ) Linked Comprehension
3 Videos
- SOLID STATEBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLID STATEEXERCISE - Exercises (Archives ) Multiple Correct
2 Videos
- SOLID STATEBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLID STATEEXERCISE - Exercises (Fill In The Blanks)
15 Videos
- REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSEXERCISE - SUBJECTIVE TYPE
4 Videos
- SOLUTIONSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLUTIONSEXERCISE - Ex 2.3 (Objective)
9 Videos
Similar Questions
In HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
If the anions (A) form hexagonal close packing and cations (C ) occupy only 2/3rd octahedral voids in it, then the general formula of the compound is
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
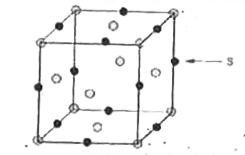
In the figure given below, the site marked as S is a
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
Mark the false statement :
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
In Schottky defect
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
In the spinel structure, oxide ions are cubic close packed whereas 1/8th of tetrahedral voids are occupied by A2+ cations and 1/2 of octahedral voids are occupied by B3+ cations. The general formula of the compound having spinel structure is
View SolutionCorrect the following statement by changing the underlined part of the sentence.
If R is the radius of the spheres forming closest packing arrangement, then radius r of the octahedral void will be 0.225 R––––––––.
View SolutionCorrect the following statement by changing the underlined part of the sentence.
If R is the radius of spheres forming closest packing arrangement, then radius r of the tetrahedral void will be 0.732R––––––––.
View SolutionIf the radius of a sphere is 2r , them its volume will be
View SolutionThe volume of a sphere is given by
V=43πR3
where R is the radius of the radius of the sphere. Find the change in volume of the sphere as the radius is increased from 10.0cm to 10.1cm. Assume that the rate does not appreciably change between R=10.0cm to R=10.1cm
View SolutionIf the radius of the octaheral void is r and the radius of the atoms in close-packing is R, derive relation between r and R
View Solution
