In HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
In the spinel structure, oxide ions are cubic close packed whereas 1/8th of tetrahedral voids are occupied by A2+ cations and 1/2 of octahedral voids are occupied by B3+ cations. The general formula of the compound having spinel structure is
A2B2O4
AB2O4
A2B4O2
A4B2O2
The correct Answer is:B
To determine the general formula of the compound with a spinel structure, we will follow these steps:
Step 1: Determine the number of oxide ions in the unit cell
In a cubic close-packed (CCP) structure, which is the same as face-centered cubic (FCC), the number of atoms (or ions) per unit cell (Z) can be calculated as follows:
- There are 8 corner atoms, each contributing 18 to the unit cell.
- There are 6 face-centered atoms, each contributing 12 to the unit cell.
Calculating the contributions:
Z=(8×18)+(6×12)=1+3=4
Thus, the number of oxide ions (O2−) per unit cell is 4.
Step 2: Determine the number of tetrahedral voids
In a close-packed structure, the number of tetrahedral voids is twice the number of atoms in the unit cell:
Number of tetrahedral voids=2×Z=2×4=8
Since 18 of the tetrahedral voids are occupied by A2+ cations:
Number of A2+ cations=18×8=1
Step 3: Determine the number of octahedral voids
The number of octahedral voids is equal to the number of atoms in the unit cell:
Number of octahedral voids=Z=4
Since 12 of the octahedral voids are occupied by B3+ cations:
Number of B3+ cations=12×4=2
Step 4: Write the general formula
Now, we can combine the contributions of the ions to write the general formula:
- Number of A2+ cations = 1
- Number of B3+ cations = 2
- Number of oxide ions = 4
Thus, the general formula of the compound is:
General formula=A1B2O4 or AB2O4
Final Answer
The general formula of the compound having a spinel structure is AB2O4.
---
In a cubic close-packed (CCP) structure, which is the same as face-centered cubic (FCC), the number of atoms (or ions) per unit cell (Z) can be calculated as follows:
- There are 8 corner atoms, each contributing 18 to the unit cell.
- There are 6 face-centered atoms, each contributing 12 to the unit cell.
Z=(8×18)+(6×12)=1+3=4
Thus, the number of oxide ions (O2−) per unit cell is 4.
In a close-packed structure, the number of tetrahedral voids is twice the number of atoms in the unit cell:
Number of tetrahedral voids=2×Z=2×4=8
Since 18 of the tetrahedral voids are occupied by A2+ cations:
Number of A2+ cations=18×8=1
The number of octahedral voids is equal to the number of atoms in the unit cell:
Number of octahedral voids=Z=4
Since 12 of the octahedral voids are occupied by B3+ cations:
Number of B3+ cations=12×4=2
Now, we can combine the contributions of the ions to write the general formula:
- Number of A2+ cations = 1
- Number of B3+ cations = 2
- Number of oxide ions = 4
General formula=A1B2O4 or AB2O4
The general formula of the compound having a spinel structure is AB2O4.
Similar Questions
In HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
Mark the false statement :
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
In Schottky defect
View Solution
Knowledge Check
In a close packed structure of mixed oxides , the lattice is composed of oxide ions , one eighth of tetrahedral voids are occupied by divalent cations while one half of octahedral voids are occupied by trivalent cations . What is the formula of the oxide ?
AA2BO4BAB2O3CA2BO3DAB2O4
In HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
In the figure given below, the site marked as S is a
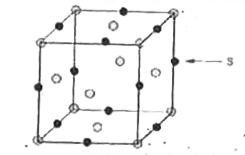
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
If the anions (A) form hexagonal close packing and cations (C ) occupy only 2/3rd octahedral voids in it, then the general formula of the compound is
View SolutionIf the radius of the spheres in the close packing is R and the radius pf pctahedral voids is r, then r=0.414R.
View SolutionIn a close packed array of N spheres, the number of tetrahedral holes are
View SolutionCorrect the following statement by changing the underlined part of the sentence.
If R is the radius of the spheres forming closest packing arrangement, then radius r of the octahedral void will be 0.225 R––––––––.
View SolutionCorrect the following statement by changing the underlined part of the sentence.
If R is the radius of spheres forming closest packing arrangement, then radius r of the tetrahedral void will be 0.732R––––––––.
View SolutionPercentage of tetrahedral voids occupied by carbon atoms per unit cell of diamond is
View Solution
