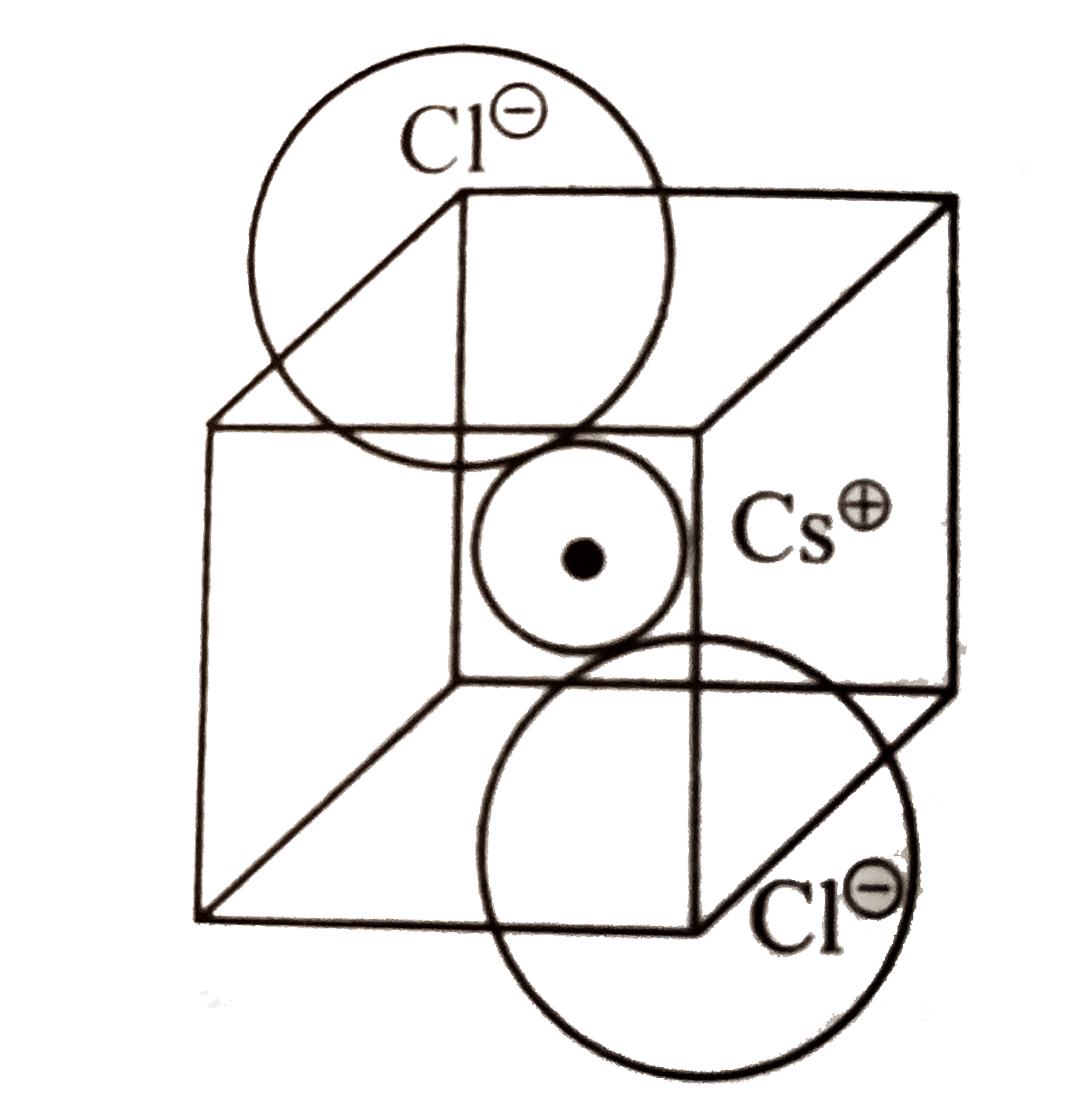
CsCl crystallises in body centred cubic lattice. If 'a' is its edge length then which of the following expression is correct ?

A

$r_{C s^{\oplus}}^{\oplus} + r_{C I^{ɵ}}^{ɵ} = \frac{\sqrt{3}}{2} a$

B

$r_{C s^{\oplus}}^{\oplus} + r_{C I^{ɵ}}^{ɵ} = \sqrt{3}$

C

$r_{C s^{\oplus}}^{\oplus} + r_{C I^{ɵ}}^{ɵ} = 3 a$

D

$r_{C s^{\oplus}}^{\oplus} + r_{C I^{ɵ}}^{ɵ} = \frac{3 a}{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$C s C l$ type is bcc ionic compound structure in which sum of their ionic radii is $\frac{\sqrt{3}}{2}$ a

|

Updated on:21/07/2023

Class 12 CHEMISTRY THE SOLID STATE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The vacant space in body centred cubic lattice unit cell is:
A0.32
B0.26
C0.48
D0.68

CENGAGE CHEMISTRY ENGLISH-SOLID STATE-Exercises (Archives ) Single Correct

Home
Ask Doubt
Profile