The plot of In c0c0−x against t is a straight line, showing the reaction to be a
Zero order reaction
First order reaction
Second order reaction
Half order reaction
The correct Answer is:B
To determine the order of the reaction based on the plot of ln(c0c0−x) against t, we can follow these steps:
Step 1: Understand the Integrated Rate Law for First-Order Reactions
For a first-order reaction, the integrated rate law can be expressed as:
ln((A)0(A))=kt
where (A)0 is the initial concentration, (A) is the concentration at time t, and k is the rate constant.
Step 2: Define Variables
Let:
- c0 = initial concentration of the reactant
- x = amount of reactant that has reacted at time t
- The concentration of the reactant at time t can be expressed as:
c=c0−x
Step 3: Substitute into the Integrated Rate Law
Substituting c0 and c into the integrated rate law gives:
ln(c0c0−x)=kt
Step 4: Analyze the Plot
The equation ln(c0c0−x)=kt indicates that if we plot ln(c0c0−x) against time t, we will obtain a straight line. The slope of this line will be equal to the rate constant k.
Step 5: Conclusion
Since the plot of ln(c0c0−x) against t is a straight line, this indicates that the reaction follows first-order kinetics.
Final Answer
The reaction is a first-order reaction.
---
For a first-order reaction, the integrated rate law can be expressed as:
ln((A)0(A))=kt
where (A)0 is the initial concentration, (A) is the concentration at time t, and k is the rate constant.
Let:
- c0 = initial concentration of the reactant
- x = amount of reactant that has reacted at time t
- The concentration of the reactant at time t can be expressed as:
c=c0−x
Substituting c0 and c into the integrated rate law gives:
ln(c0c0−x)=kt
The equation ln(c0c0−x)=kt indicates that if we plot ln(c0c0−x) against time t, we will obtain a straight line. The slope of this line will be equal to the rate constant k.
Since the plot of ln(c0c0−x) against t is a straight line, this indicates that the reaction follows first-order kinetics.
The reaction is a first-order reaction.
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Solved Example
52 Videos
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Ex 4.1 (Objective)
9 Videos
- CARBOXYLIC ACIDS AND THEIR DERIVATIVESBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CARBOXYLIC ACIDS AND THEIR DERIVATIVESEXERCISE - Exercises Archives (Analytical And Descriptive)
34 Videos
- COORDINATION COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - COORDINATION COMPOUNDSEXERCISE - Archives Subjective
18 Videos
Similar Questions
Knowledge Check
A plot of log (a-x) against time 't' is a straight line. This indicates that the reaction is of :
Azero orderBfirst orderCsecond orderDthird order
A plot of ln k against 1T (abscissa) is expected to be a straight line with intercept on coordinate axis equal to
View SolutionPlot of log(x/m) against log P is a straight line inclined at an angle of 45∘. When the pressure is 0.5 atm and Freundlich parameter ,K is 10, the amount of solute adsorbed per gram of adsorbent will be : (log 5=0.6990 )
View SolutionIn the reaction A+B→C+D, the rate (dxdt) when plotted against time 't' gives a straight line parallel to time aixs.
The order and rate of reaction will be:
View SolutionFreundlich adsorption isotherm gives a straight line on plotting :
View SolutionFor a lst order reaction , a straight line is obtained if you plot
View SolutionIn a second order reaction, the plot of 1/(a−x) versus t is a straight line.
View SolutionVelocity-time graph of a particle moving in a straight line is shown in figure. At time t=0,s=−10m. Plot corresponding a-t and s-t graphs.
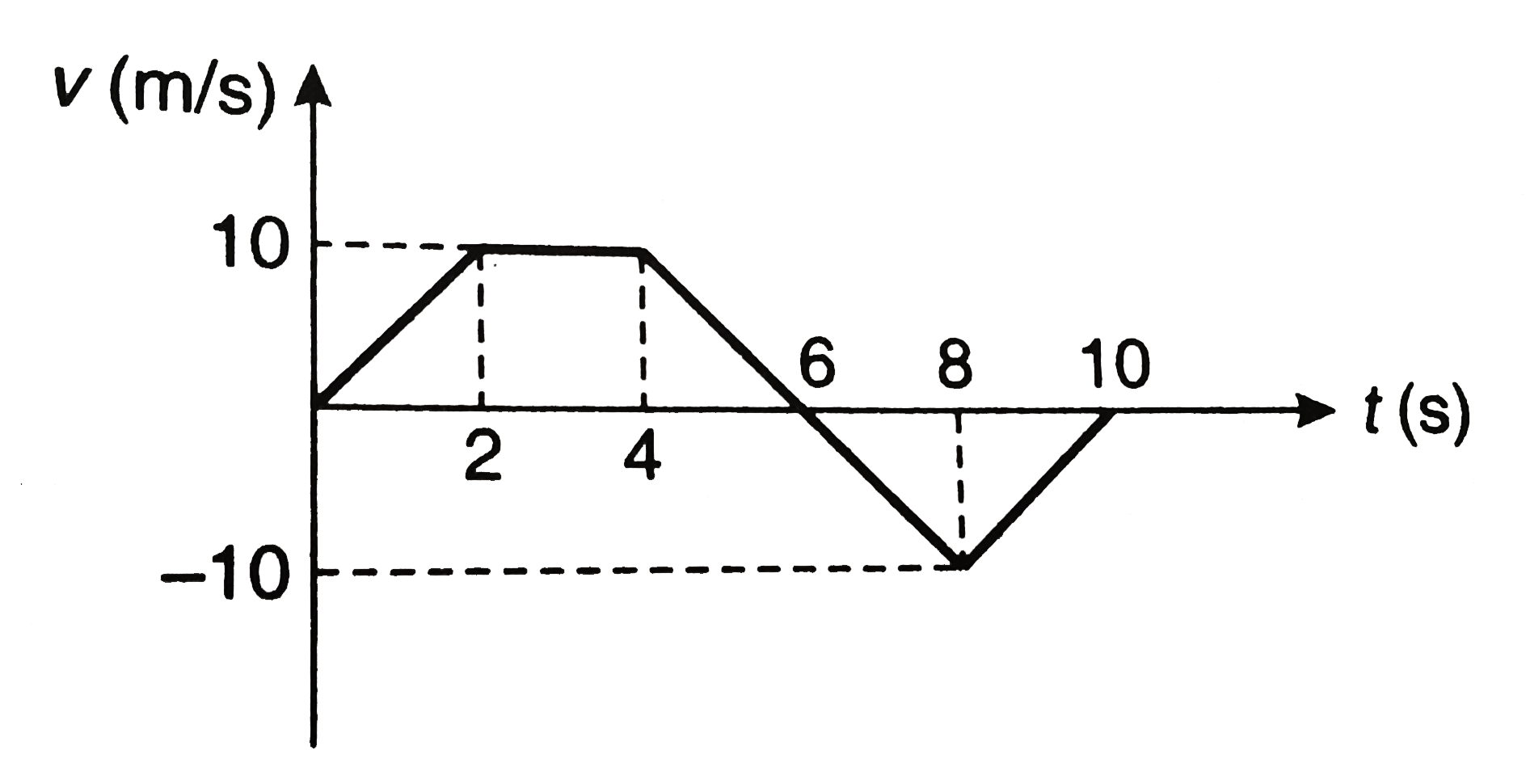
View Solution
