A reaction takes place in theee steps: the rate constant are k1,k2,andk3. The overall rate constant k=k1k3/k2. If the energies of activation are 40,30,and20KJmol−1, the overall energy of activation is (assuming A to be constant for all)
10
15
30
60
The correct Answer is:c
To solve the problem, we need to find the overall energy of activation for a reaction that occurs in three steps with given activation energies and a specific relationship between the rate constants. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the relationship between rate constants
The overall rate constant k is given by:
k=k1⋅k3k2
Step 2: Use the Arrhenius equation
According to the Arrhenius equation, the rate constant k can be expressed in terms of the activation energy Ea as follows:
k=Ae−EaRT
where A is the pre-exponential factor, Ea is the activation energy, R is the universal gas constant, and T is the temperature in Kelvin.
Step 3: Substitute the Arrhenius equation into the rate constant relationship
Substituting the Arrhenius equation into the expression for k:
k=Ae−Ea1RT⋅Ae−Ea3RT⋅1Ae−Ea2RT
Step 4: Simplify the equation
This simplifies to:
k=A2e−Ea1RT⋅e−Ea3RT⋅eEa2RT
Combining the exponents:
k=A2e−Ea1+Ea3−Ea2RT
Step 5: Identify the overall activation energy
From the above equation, we can identify the overall activation energy Ea for the reaction as:
Ea=Ea1+Ea3−Ea2
Step 6: Substitute the given activation energies
We are given:
- Ea1=40kJ/mol
- Ea2=30kJ/mol
- Ea3=20kJ/mol
Substituting these values into the equation:
Ea=40+20−30
Ea=30kJ/mol
Final Answer
The overall energy of activation is 30kJ/mol.
---
The overall rate constant k is given by:
k=k1⋅k3k2
According to the Arrhenius equation, the rate constant k can be expressed in terms of the activation energy Ea as follows:
k=Ae−EaRT
where A is the pre-exponential factor, Ea is the activation energy, R is the universal gas constant, and T is the temperature in Kelvin.
Substituting the Arrhenius equation into the expression for k:
k=Ae−Ea1RT⋅Ae−Ea3RT⋅1Ae−Ea2RT
This simplifies to:
k=A2e−Ea1RT⋅e−Ea3RT⋅eEa2RT
Combining the exponents:
k=A2e−Ea1+Ea3−Ea2RT
From the above equation, we can identify the overall activation energy Ea for the reaction as:
Ea=Ea1+Ea3−Ea2
We are given:
- Ea1=40kJ/mol
- Ea2=30kJ/mol
- Ea3=20kJ/mol
Ea=40+20−30
Ea=30kJ/mol
The overall energy of activation is 30kJ/mol.
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Solved Example
52 Videos
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Ex 4.1 (Objective)
9 Videos
- CARBOXYLIC ACIDS AND THEIR DERIVATIVESBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CARBOXYLIC ACIDS AND THEIR DERIVATIVESEXERCISE - Exercises Archives (Analytical And Descriptive)
34 Videos
- COORDINATION COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - COORDINATION COMPOUNDSEXERCISE - Archives Subjective
18 Videos
Similar Questions
A reaction takes place in theee steps: the rate constant are k1,k2,andk3. The overall rate constant k=k1k3k2. If E1,E2, and E3 (energy of activation) are 60,30 and 10kJ, respectively, the overall energy of activation is
View SolutionA reaction takes place in various steps. The rate constatn for first, second, third and fifth steps are k1,k2,k3 and k5 respectively The overall rate constant is given by
k=k2k3(k1k5)1/2
If activation energy are 40, 60, 50, and 10 kJ/mol respectively, the overall energy of activation (kJ/mol) is :
View SolutionThe rate constants k1 and k2 of two reactions are in the ratio 2:1. The corresponding energies of acativation of the two reaction will be related by
View SolutionRate constant for a chemical reaction taking place at 500K is expressed as K=A.e−1000 The activation energy of the reaction is :
View SolutionFor a reaction, the rate constant is expressed as k=Ae−40000/T. The energy of the activation is
View SolutionA chemical reaction was carried out at 300 K and 280 K. The rate constants were found to be k1andk2 respectively. Then
View SolutionRate of two reaction whose rate constants arek1&k2 are equal at 300 k such that: So caculate ln(A2)A1=? Ea2−Ea1=2RT.
View SolutionIf the rate constant k of a reaction is 1.6×10–3(mol/l)(–min1) . The order of the reaction is:
View SolutionFor a reaction, activation energy (E_a ) =0 and rate constant, k=1.5x104s−1 at 300 K. What is the value of rate constant at 320 K'?
View SolutionA colliison between reactant molecules must occur with a certain minimum energy before it is effective in yielding Product molecules. This minimum energy is called activation energy Ea Large the value of activation energy, smaller the value of rate constant k. Larger is the value of activation energy, greater is the effect of temperature rise on rate constant k.
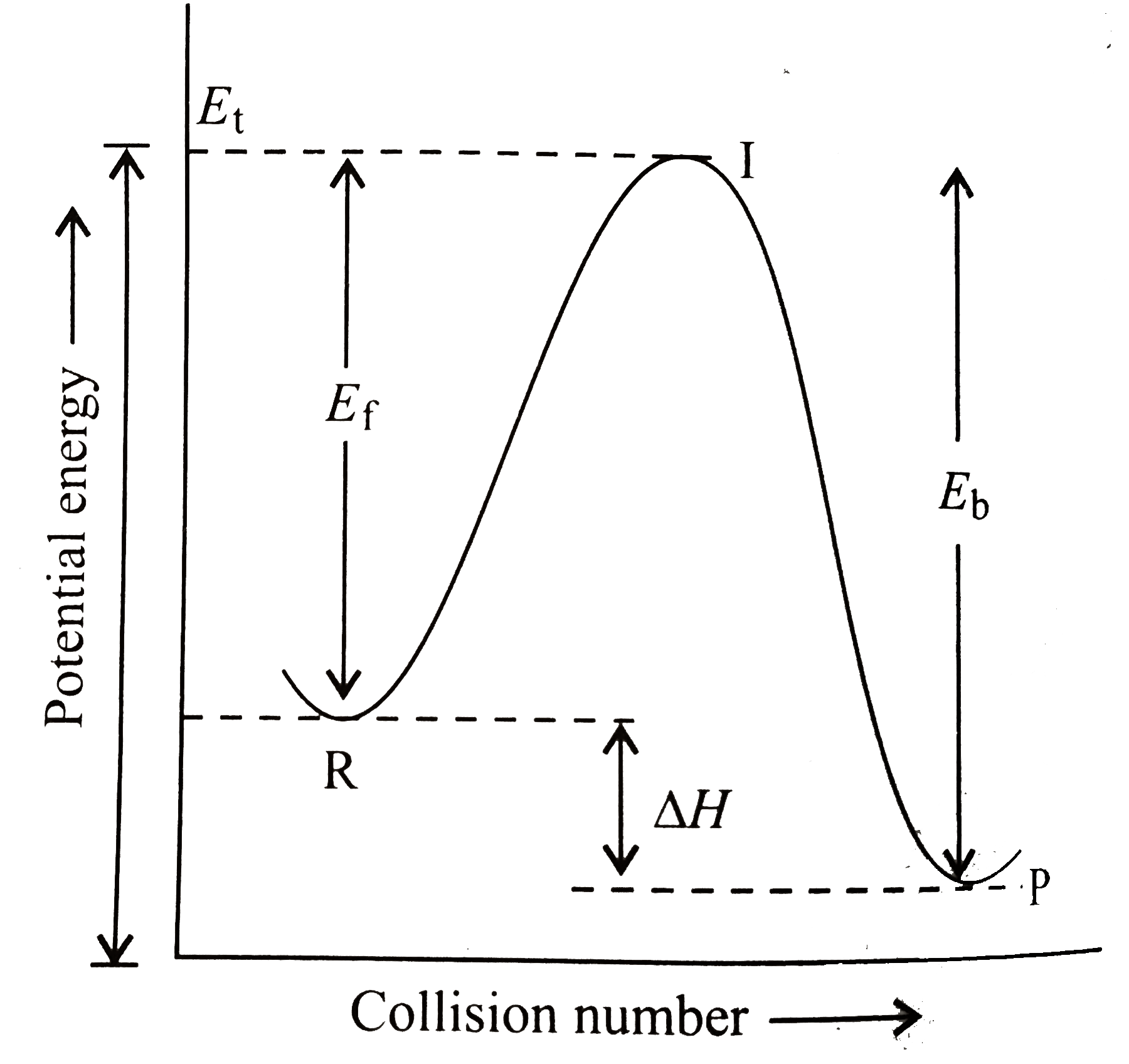
Ef= Activation energy of forward reaction
Eb= Activation energy of backward reaction
ΔH=Ef−Eb
Ef= threshold energy
For two reactions, activation energies are Ea1 and Ea2, rate constant are k1 and k2 at the same temperature. If k1>k2, then
View Solution
