The activation energy of a first order reaction at 300K is 60 kJmol−1. In the presence of a catalyst, the activation energy gets lowered to 50kJmol−1 at 300K. How many times the reaction rate change in the presence of a catalyst at the same temperature ?
To solve the problem of how many times the reaction rate changes in the presence of a catalyst, we can use the Arrhenius equation and the relationship between the rate constants of the reaction with and without the catalyst.
1. Identify Given Data:
- Activation energy without catalyst (Ea1) = 60 kJ/mol = 60000 J/mol
- Activation energy with catalyst (Ea2) = 50 kJ/mol = 50000 J/mol
- Temperature (T) = 300 K
- Universal gas constant (R) = 8.314 J/(mol·K)
2. Use the Arrhenius Equation:
The Arrhenius equation relates the rate constants (k) to the activation energy (Ea) and temperature (T):
k=Ae−EaRT
Where A is the pre-exponential factor.
3. Calculate the Rate Constants (k1 and k2):
We can express the ratio of the rate constants (k2/k1) as follows:
k2k1=Ae−Ea2RTAe−Ea1RT=e−Ea2RT/e−Ea1RT=e(Ea1−Ea2RT)
4. Substitute Values:
Now, substituting the values into the equation:
k2k1=e(60000J/mol−50000J/mol8.314J/(mol⋅K)×300K)
Simplifying the exponent:
k2k1=e(100002494.2)≈e4.008
5. Calculate the Exponential:
Now calculate e4.008:
e4.008≈55.08
6. Conclusion:
Therefore, the reaction rate increases by approximately 55 times in the presence of the catalyst.
Final Answer:
The reaction rate increases by approximately 55 times in the presence of a catalyst at the same temperature.
- Activation energy without catalyst (Ea1) = 60 kJ/mol = 60000 J/mol
- Activation energy with catalyst (Ea2) = 50 kJ/mol = 50000 J/mol
- Temperature (T) = 300 K
- Universal gas constant (R) = 8.314 J/(mol·K)
The Arrhenius equation relates the rate constants (k) to the activation energy (Ea) and temperature (T):
k=Ae−EaRT
Where A is the pre-exponential factor.
We can express the ratio of the rate constants (k2/k1) as follows:
k2k1=Ae−Ea2RTAe−Ea1RT=e−Ea2RT/e−Ea1RT=e(Ea1−Ea2RT)
Now, substituting the values into the equation:
k2k1=e(60000J/mol−50000J/mol8.314J/(mol⋅K)×300K)
Simplifying the exponent:
k2k1=e(100002494.2)≈e4.008
Now calculate e4.008:
e4.008≈55.08
Therefore, the reaction rate increases by approximately 55 times in the presence of the catalyst.
The reaction rate increases by approximately 55 times in the presence of a catalyst at the same temperature.
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Solved Example
52 Videos
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Ex 4.1 (Objective)
9 Videos
- CARBOXYLIC ACIDS AND THEIR DERIVATIVESBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CARBOXYLIC ACIDS AND THEIR DERIVATIVESEXERCISE - Exercises Archives (Analytical And Descriptive)
34 Videos
- COORDINATION COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - COORDINATION COMPOUNDSEXERCISE - Archives Subjective
18 Videos
Similar Questions
The activation energy for a first order reaction is 60 kJ mol−1 in the absence of a catalyst and 50 kJ mol−1 in the presence of a catalyst. How many times will the rate of reaction grow in the presence of the catalyst if the reaction proceeds at 27∘C ?
View SolutionThe activation energy for a first order reaction is 60 kJ mol−1 in the absence of a catalyst and 50 kJ mol−1 in the presence of a catalyst. How many times will the rate of reaction grow in the presence of the catalyst if the reaction proceeds at 27∘C ?
View SolutionThe activation energy for a first order reaction is 60 kJ mol−1 in the absence of a catalyst and 50 kJ mol−1 in the presence of a catalyst. How many times will the rate of reaction grow in the presence of the catalyst if the reaction proceeds at 27∘C ?
View SolutionA catalyst lowered the activation energy byh 25KJmol−1 at 25∘C . By how many times will the rate grow?
View SolutionThe activation energy of a reaction is 75.2 kJ mol−1 in the absence of a catalyst and 50.14 kJ mol−1 with a catalyst. How many times will the rate of reaction grow in the presence of the catalyst if the reaction proceeds at 25∘C?[R=8.314JK−1 mole1 ]
View SolutionThe activation energy of a reaction is 75.2 kJ mol−1 in the absence of a catalyst and 50.14 kJ mol−1 with a catalyst. How many times will the rate of reaction grow in the presence of the catalyst if the reaction proceeds at 25∘C?[R=8.314JK−1 mole1 ]
View SolutionThe activation energy of a reaction is 75.2 kJ mol−1 in the absence of a catalyst and 50.14 kJ mol−1 with a catalyst. How many times will the rate of reaction grow in the presence of the catalyst if the reaction proceeds at 25∘C?[R=8.314JK−1 mole1 ]
View SolutionThe activation energy for the forward reaction X→Y is 60kJmol−1 and ΔH is −20kJmol−1. The activation energy for the reverse reaction is
View SolutionThe major product of the following reaction is:
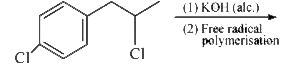
View SolutionThe activation energy of
H2+I2⇔2HI(g) in equilibrium for the forward reaction is 167kJmol−1 whereas for the reverse reaction is 180kJmol−1. The presence of catalyst lowers the activation energy by 80kJmol−1. Assuming that the reactions are made at 27∘C and the frequency factor for forwatd and backward reactions are 4×10−4 and 2×10−3 respectively, calculate Kc.
View Solution
