At 400K , the energy of activation of a reaction is decreased by 0.8Kcal in the presence of catalyst. Hence, the rate will be
a. Increased by 2.73 times
b. Increased by 1.18 times
c. Decreased by 2.72 times
d. Increased by 6.26 times
To solve the problem, we will use the Arrhenius equation, which relates the rate constant of a reaction to its activation energy and temperature. The steps are as follows:
1. Understand the given data:
- Activation energy decrease (ΔE) = -0.8 kcal = -0.8 × 10³ cal
- Temperature (T) = 400 K
2. Convert the activation energy to calories:
- Since 1 kcal = 1000 cal, the decrease in activation energy is:
ΔE=−0.8×103 cal
3. Use the Arrhenius equation:
- The Arrhenius equation can be expressed in logarithmic form as:
log(K2K1)=−Ea2.303RT
- Where:
- K1 = rate constant without catalyst
- K2 = rate constant with catalyst
- Ea = activation energy
- R = universal gas constant (2 cal/K·mol)
- T = temperature in Kelvin
4. Substituting the values into the equation:
- Substitute Ea=0.8×103 cal, R=2 cal/K·mol, and T=400 K into the equation:
log(K2K1)=−0.8×1032.303×2×400
5. Calculate the denominator:
- Calculate 2.303×2×400:
2.303×2×400=1842.4
6. Calculate the logarithm:
- Now substitute this value back into the equation:
log(K2K1)=−8001842.4≈−0.434
7. Convert logarithm to ratio:
- To find the ratio K2K1:
K2K1=10−0.434≈2.71
8. Relate the rate constants to reaction rates:
- Since the rate of the reaction is directly proportional to the rate constant, we can say:
R2R1=K2K1≈2.71
9. Conclusion:
- The rate of the reaction increases by approximately 2.71 times, which corresponds to option (a).
Final Answer:
The rate will be increased by approximately 2.73 times (option a).
- Activation energy decrease (ΔE) = -0.8 kcal = -0.8 × 10³ cal
- Temperature (T) = 400 K
- Since 1 kcal = 1000 cal, the decrease in activation energy is:
ΔE=−0.8×103 cal
- The Arrhenius equation can be expressed in logarithmic form as:
log(K2K1)=−Ea2.303RT
- Where:
- K1 = rate constant without catalyst
- K2 = rate constant with catalyst
- Ea = activation energy
- R = universal gas constant (2 cal/K·mol)
- T = temperature in Kelvin
- Substitute Ea=0.8×103 cal, R=2 cal/K·mol, and T=400 K into the equation:
log(K2K1)=−0.8×1032.303×2×400
- Calculate 2.303×2×400:
2.303×2×400=1842.4
- Now substitute this value back into the equation:
log(K2K1)=−8001842.4≈−0.434
- To find the ratio K2K1:
K2K1=10−0.434≈2.71
- Since the rate of the reaction is directly proportional to the rate constant, we can say:
R2R1=K2K1≈2.71
- The rate of the reaction increases by approximately 2.71 times, which corresponds to option (a).
The rate will be increased by approximately 2.73 times (option a).
Topper's Solved these Questions
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SURFACE CHEMISTRYEXERCISE - Illustration 5.361videos
SURFACE CHEMISTRY
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SURFACE CHEMISTRYEXERCISE - Solved Examples20videos
SURFACE CHEMISTRY
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLUTIONSEXERCISE - Ex 2.3 (Objective)9videos
SOLUTIONS
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SYNTHETIC AND NATURAL POLYMERSEXERCISE - Exercises Assertion Reasoning10videos
SYNTHETIC AND NATURAL POLYMERS
Similar Questions
If concentration of reactant is increased by 2 times then K
becomes :-View SolutionAt 227∘C , the presence of catalyst causes the activation energy of a reaction to decrease by 4.606Kcal.The rate of the reaction will be increased by :−
View SolutionThe solution of CuSO4 in which Cu ord is dipped is diluted to 10 times, the reduction electrode potential will :
a. Decrease by 0.03V b. Decrease by 0.059V
c. Increase by 0.03V d. Increase by −.059VView SolutionGiven : A⇔B+C,ΔH=−10 kcals, the energy of activation of backward reaction is 15 kcal mol−1. If the energy of activation of forward reaction in the presence of a catalyst is 3 kcal mol−1 the catalyst will increase the rate of reaction at 300 K by the number of times equal to
View SolutionAssertion: A catalyst increases the rate of a reaction.
Reason: In presence of a catalyst, the activation energy of the reaction decreases.View SolutionWhen the concentration of a reactant in reaction A→B is increased by 8 times but rate increases only 2 times, the order of the reaction would be
View SolutionThe major product of the following reaction is:
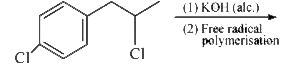 View Solution
View SolutionIn the presence of a catalyst, the rate of a reaction grows to the extent of 105 times at 298K. Hence, the catalyst must have lowered Ea by
View SolutionIf the rate of reaction increases by 27 times , when temperature is increased by 30 K, then temperature coefficient of the reaction is
View SolutionFor the chemical reaction X→Y, it is found that the rate of reaction increases by 2.25 times when the concentration of X is increased by 1.5 times, what is the order w.r.t. X ?
View Solution

