In the presence of a catalyst, the rate of a reaction grows to the extent of times at . Hence, the catalyst must have lowered by
The correct Answer is:D
To solve the problem, we need to determine how much the activation energy (Ea) has been lowered by a catalyst, given that the rate of reaction increases by a factor of 105 at a temperature of 298 K.
1. Understanding the Relationship Between Rate Constants and Activation Energy:
The rate constant k for a reaction can be expressed using the Arrhenius equation:
k=Ae−EaRT
where:
- A is the pre-exponential factor,
- Ea is the activation energy,
- R is the universal gas constant (8.314 J/mol·K),
- T is the temperature in Kelvin.
2. Setting Up the Problem:
We have two rate constants, k1 and k2, corresponding to the reaction rates before and after the introduction of the catalyst. Given that the rate increases by a factor of 105, we can express this as:
k2k1=105
3. Using the Arrhenius Equation:
We can express the ratio of the rate constants using the Arrhenius equation:
k2k1=Ae−Ea2RTAe−Ea1RT=e−Ea2−Ea1RT
This simplifies to:
k2k1=e−ΔEaRT
where ΔEa=Ea2−Ea1.
4. Taking the Natural Logarithm:
Taking the natural logarithm of both sides gives:
ln(k2k1)=−ΔEaRT
5. Substituting Known Values:
We know:
- k2k1=105
- R=8.314J/mol⋅K
- T=298K
Therefore:
ln(105)=5ln(10)≈5×2.303≈11.515
6. Rearranging the Equation:
Now substituting into the equation:
11.515=−ΔEa(8.314)(298)
7. Calculating ΔEa:
Rearranging gives:
ΔEa=−11.515×(8.314)×(298)
Calculating this:
ΔEa=−11.515×2477.572≈−28566.2J/mol≈−28.566kJ/mol
8. Final Answer:
Rounding to two decimal places, the catalyst must have lowered the activation energy by approximately:
ΔEa≈−28.5kJ/mol
Conclusion:
The catalyst must have lowered the activation energy by approximately 28.5 kJ/mol.
The rate constant k for a reaction can be expressed using the Arrhenius equation:
k=Ae−EaRT
where:
- A is the pre-exponential factor,
- Ea is the activation energy,
- R is the universal gas constant (8.314 J/mol·K),
- T is the temperature in Kelvin.
We have two rate constants, k1 and k2, corresponding to the reaction rates before and after the introduction of the catalyst. Given that the rate increases by a factor of 105, we can express this as:
k2k1=105
We can express the ratio of the rate constants using the Arrhenius equation:
k2k1=Ae−Ea2RTAe−Ea1RT=e−Ea2−Ea1RT
This simplifies to:
k2k1=e−ΔEaRT
where ΔEa=Ea2−Ea1.
Taking the natural logarithm of both sides gives:
ln(k2k1)=−ΔEaRT
We know:
- k2k1=105
- R=8.314J/mol⋅K
- T=298K
ln(105)=5ln(10)≈5×2.303≈11.515
Now substituting into the equation:
11.515=−ΔEa(8.314)(298)
Rearranging gives:
ΔEa=−11.515×(8.314)×(298)
Calculating this:
ΔEa=−11.515×2477.572≈−28566.2J/mol≈−28.566kJ/mol
Rounding to two decimal places, the catalyst must have lowered the activation energy by approximately:
ΔEa≈−28.5kJ/mol
The catalyst must have lowered the activation energy by approximately 28.5 kJ/mol.
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Exercises Linked Comprehension
59 Videos
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Exercises Multiple Correct
33 Videos
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Ex 4.3 More Than One Correct
5 Videos
- CARBOXYLIC ACIDS AND THEIR DERIVATIVESBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CARBOXYLIC ACIDS AND THEIR DERIVATIVESEXERCISE - Exercises Archives (Analytical And Descriptive)
34 Videos
- COORDINATION COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - COORDINATION COMPOUNDSEXERCISE - Archives Subjective
18 Videos
Similar Questions
The activation energy for a first order reaction is 60 kJ mol−1 in the absence of a catalyst and 50 kJ mol−1 in the presence of a catalyst. How many times will the rate of reaction grow in the presence of the catalyst if the reaction proceeds at 27∘C ?
View SolutionThe activation energy for a first order reaction is 60 kJ mol−1 in the absence of a catalyst and 50 kJ mol−1 in the presence of a catalyst. How many times will the rate of reaction grow in the presence of the catalyst if the reaction proceeds at 27∘C ?
View SolutionThe activation energy for a first order reaction is 60 kJ mol−1 in the absence of a catalyst and 50 kJ mol−1 in the presence of a catalyst. How many times will the rate of reaction grow in the presence of the catalyst if the reaction proceeds at 27∘C ?
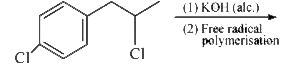
View SolutionThe major product of the following reaction is:
View SolutionThe activation energy of a first order reaction at 300K is 60 kJmol−1. In the presence of a catalyst, the activation energy gets lowered to 50kJmol−1 at 300K. How many times the reaction rate change in the presence of a catalyst at the same temperature ?
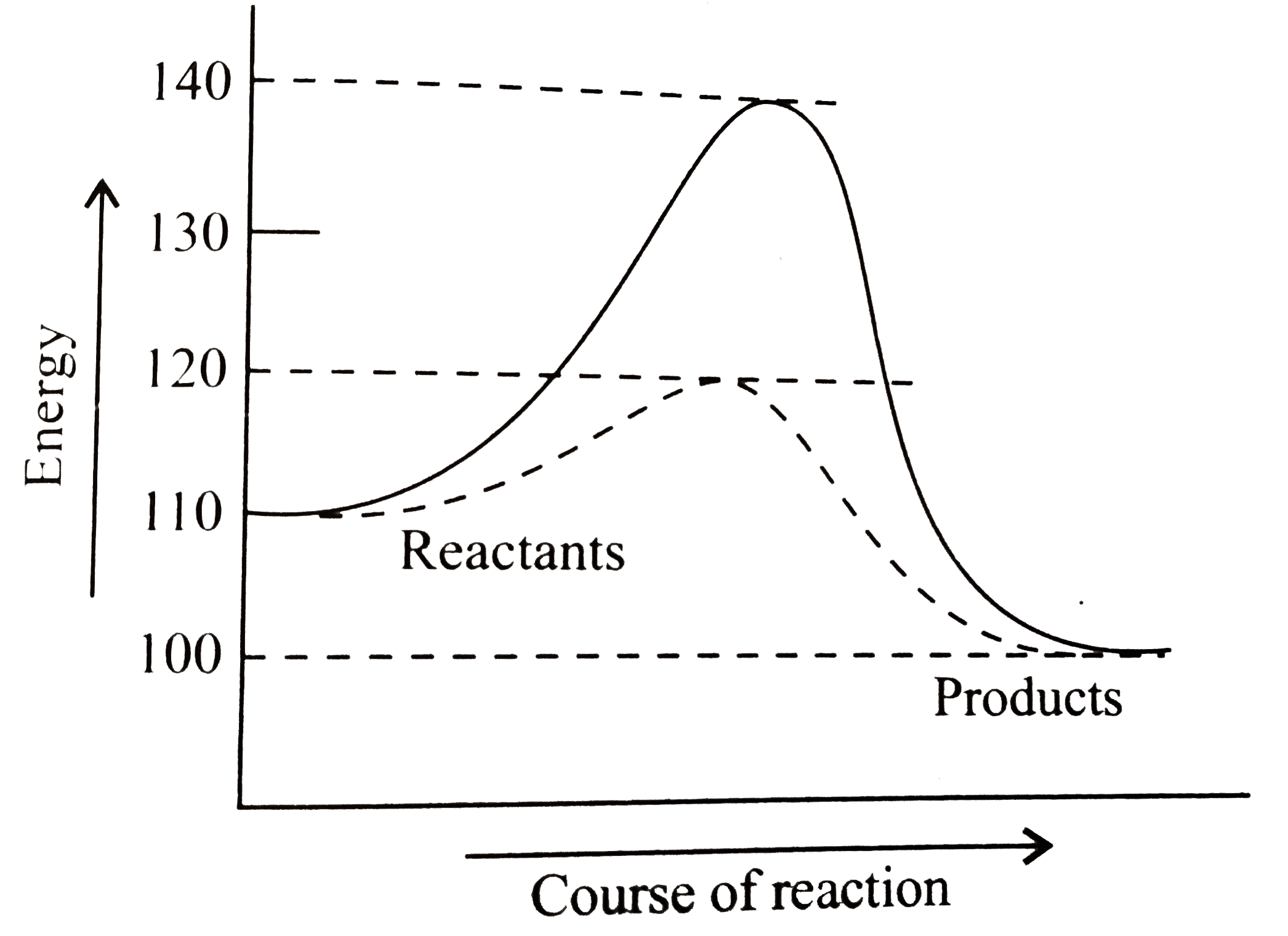
View SolutionRefer picture given below.
(a) Calculate ΔH for the reaction and the energy of activation for the forward reaction as well as backward reaction.
(b) The dotted curve is in the presence of a catalyst. What is the energy of activation for the two reactions in the presence of catalyst?
( c) Will the catalyst change the extent of reaction?
View SolutionAt 227∘C , the presence of catalyst causes the activation energy of a reaction to decrease by 4.606Kcal.The rate of the reaction will be increased by :−
View SolutionHow do temperature and the presence of a catalyst bring about an increase in the rate of a reaction ?
View SolutionAssertion(A): The pressence of a catalyst increases the speed of the forward and backward reactions to the same extent.
Reason(R): Activation energy for both the forward and backward reactions is lowered to same extent.
View SolutionThe activation energy of a reaction is 75.2 kJ mol−1 in the absence of a catalyst and 50.14 kJ mol−1 with a catalyst. How many times will the rate of reaction grow in the presence of the catalyst if the reaction proceeds at 25∘C?[R=8.314JK−1 mole1 ]
View Solution
