The optical rotation of an optically active compound is +20∘. The length of tube is 10cm and the density of solution is 0.4gmml−. The specific rotation of the compound is:
i. +50∘ ii. +500∘ iii. +5∘ iv. +0.5∘
To find the specific rotation of the optically active compound, we can use the formula for observed rotation:
αobserved=(α)⋅C⋅L
Where:
- αobserved is the observed rotation (given as +20∘),
- (α) is the specific rotation (what we need to find),
- C is the concentration of the solution in grams per milliliter (given as 0.4g/ml),
- L is the length of the tube in decimeters (given as 10cm, which is equal to 1dm).
1. Convert the length of the tube from centimeters to decimeters:
L=10cm=1dm
2. Substitute the known values into the formula:
αobserved=(α)⋅C⋅L
+20∘=(α)⋅(0.4g/ml)⋅(1dm)
3. Rearrange the formula to solve for specific rotation (α):
(α)=αobservedC⋅L
4. Substitute the values into the rearranged formula:
(α)=+20∘0.4⋅1
5. Calculate the specific rotation:
(α)=+20∘0.4=+50∘
Conclusion:
The specific rotation of the compound is +50∘.
Answer:
i. +50∘
- αobserved is the observed rotation (given as +20∘),
- (α) is the specific rotation (what we need to find),
- C is the concentration of the solution in grams per milliliter (given as 0.4g/ml),
- L is the length of the tube in decimeters (given as 10cm, which is equal to 1dm).
L=10cm=1dm
αobserved=(α)⋅C⋅L
+20∘=(α)⋅(0.4g/ml)⋅(1dm)
(α)=αobservedC⋅L
(α)=+20∘0.4⋅1
(α)=+20∘0.4=+50∘
The specific rotation of the compound is +50∘.
i. +50∘
Topper's Solved these Questions
- ISOMERISMBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ISOMERISMEXERCISE - Example
15 Videos
- ISOMERISMBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ISOMERISMEXERCISE - Exercise
19 Videos
- IONIC EQUILIBRIUMBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - IONIC EQUILIBRIUMEXERCISE - Archives Subjective
28 Videos
- NCERT BASED EXERCISEBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - NCERT BASED EXERCISEEXERCISE - Chemical Equilibrium
73 Videos
Similar Questions
The observed rotation of 2.0 gm of a compound in 10 mL solution in
a 25 cm long polarimeter tube is +13.4∘ . The specific
rotation of compound is :
View SolutionThe specific conductance of saturated solution of CaF2 is 3.86×10−5mhocm−1 and that of water used for solution is 0.15×10−5. The specific conductance of CaF2 alone is
View Solution
Knowledge Check
The observed rotation of 2.0 gm of a compound in 10 mL solution in
a 25 cm long polarimeter tube is +13.4∘ . The specific
rotation of compound is :A+30.2∘B−26.8∘C+26.8∘D+40.2∘
The length of the tube of a microscope is 10 cm . The focal lengths of the objective and eye lenses are 0.5 cm and 1.0 cm . The magnifying power of the microscope is about
View SolutionFind the cube of : (i) 225 (ii) 314 (iii) 0.3 (iv) 1.5
View SolutionCalculate the molality of potassium carbonate solution which is formed by dissolving 2.5 gm of it in one litre solution. (density of solution of 0.85 g/mL).
View SolutionDraw the graph of each of the following equations:
(i) y=3 (ii) y+5=0 (iii) x=4 (iv) x=6=0
View SolutionOptical rotations of some compounds alongwith their structures are given below which of them have D configuration.
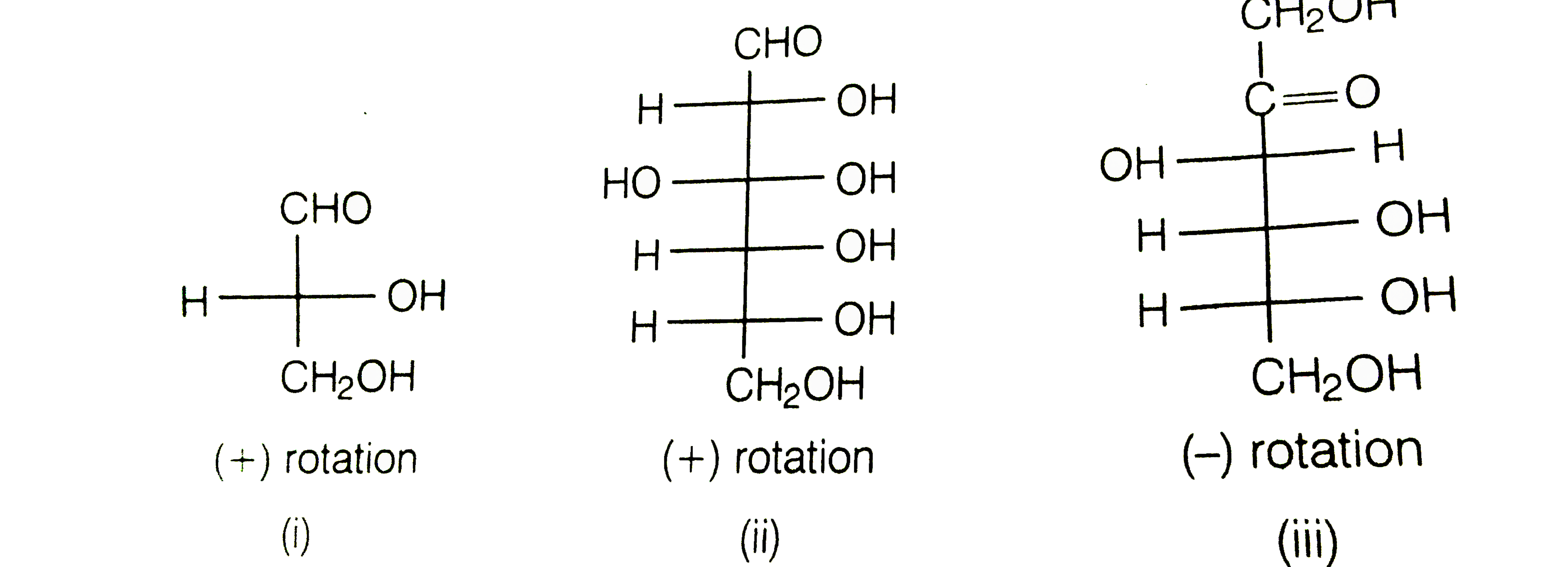
(a)I,II,III
(b)II,III
(c)I,II
(d)III
View Solution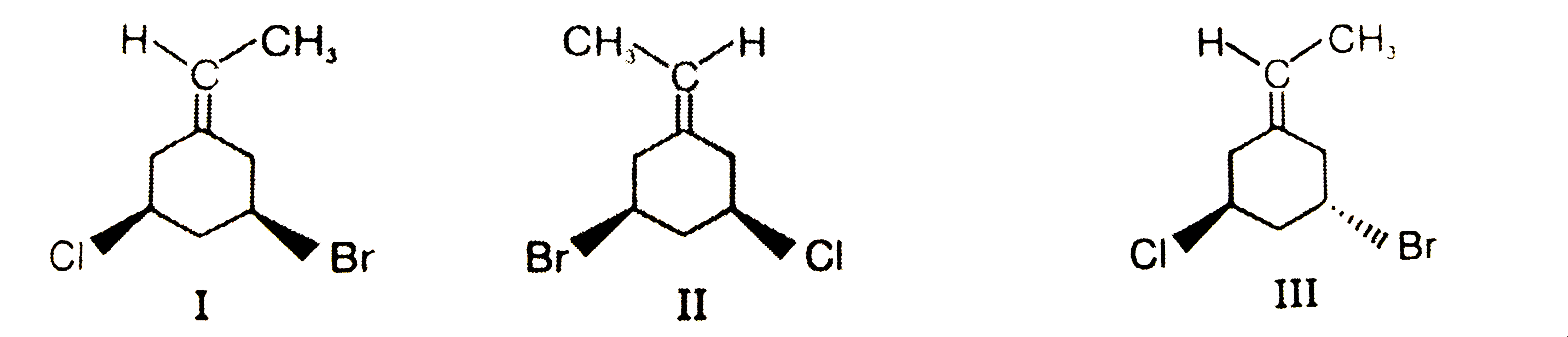 (i) Total number of tractions on fractional distillation of I, II and III. (ii) Optical active compounds.
(i) Total number of tractions on fractional distillation of I, II and III. (ii) Optical active compounds.
(iii) Relation between I and II. (iv) Relation between I and II.
View SolutionCompound which rotates the plane polarised light is known as optically active compound . On the basis of direction of rotation two forms of an optically active compounds are termed as dextro and laevo rotatory . The two are termed as enantiomers . If we have a 1 : 1 mixture of d and l isomers of a given chiral compound , optical rotation of such mixture is zero Such a mixture is optically inactive and is called a recemic modification.
The net specific rotation of any mixture of the d and isomers of a given chiral compound is equal to the weighted average of the rotations due to both the isomers Mathematically if can be expressed as :
[α]≠t=fd[αd]+f1[αl]
Where fa and fl are fractions of d and l isomers respectively and [αd],[αl] are their specific rotations
The pure d isomer of certain chiral compound has
[α]25d=+55∘.A non racemic mixture of this compound has a net [α]25d=−11∘. What is the fractions of this isomer in mixture ?
View Solution
