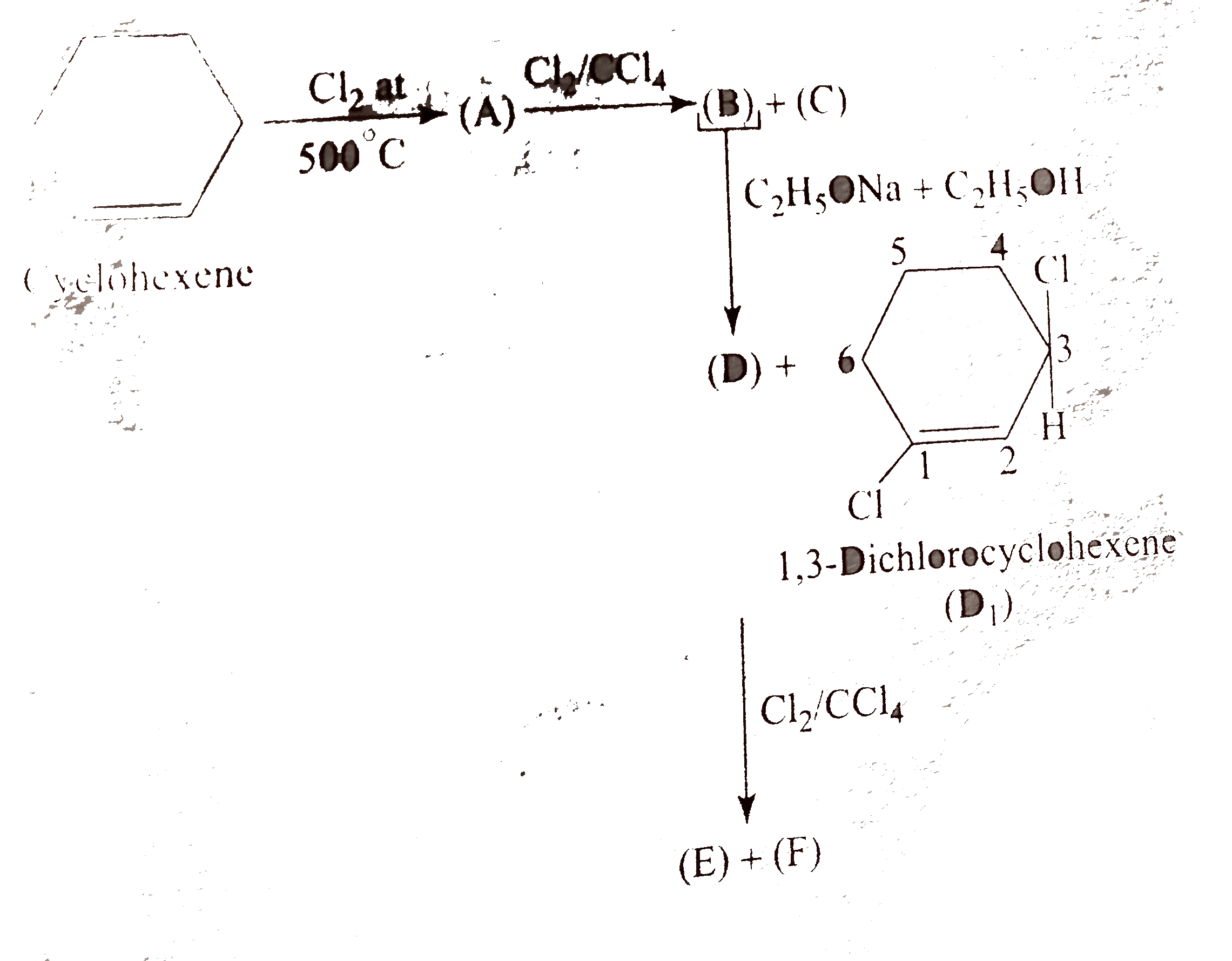
(E) and (F), respectively, are :
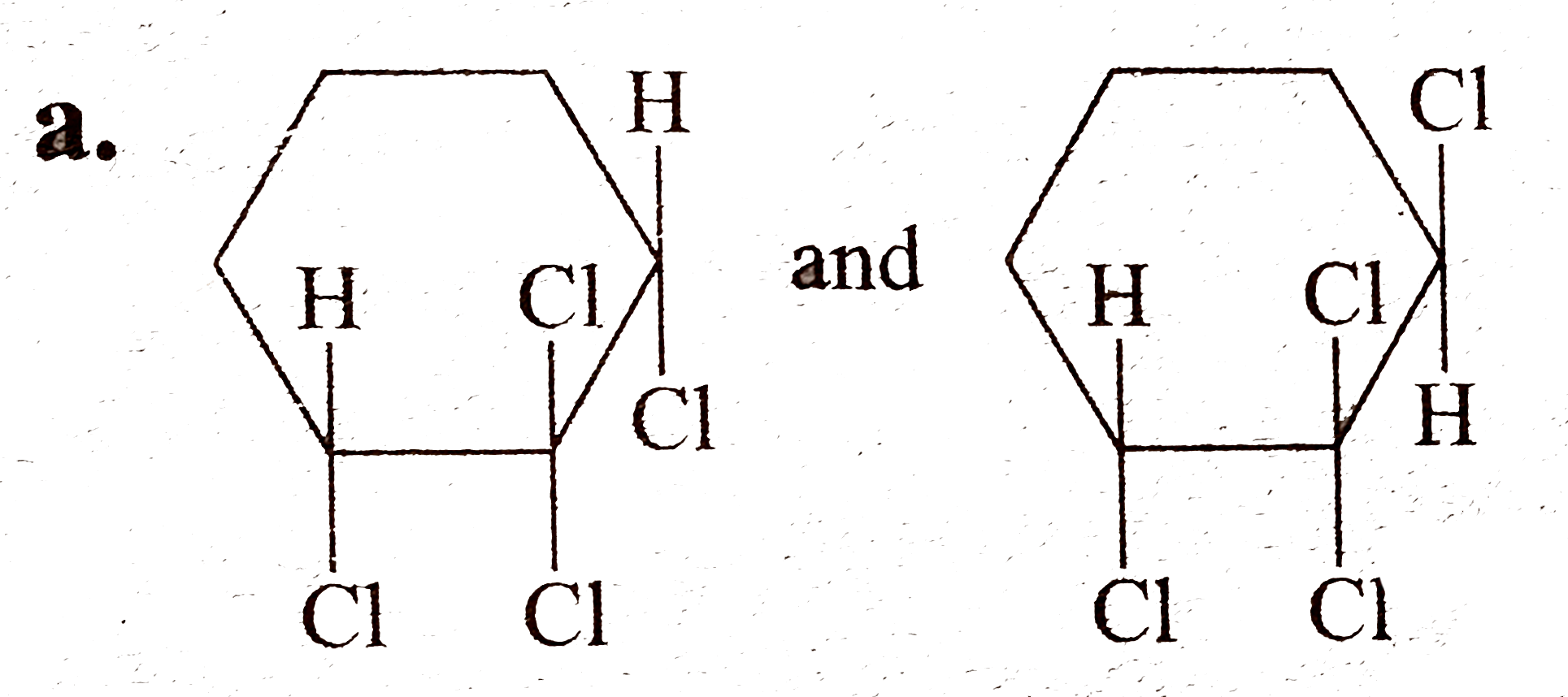
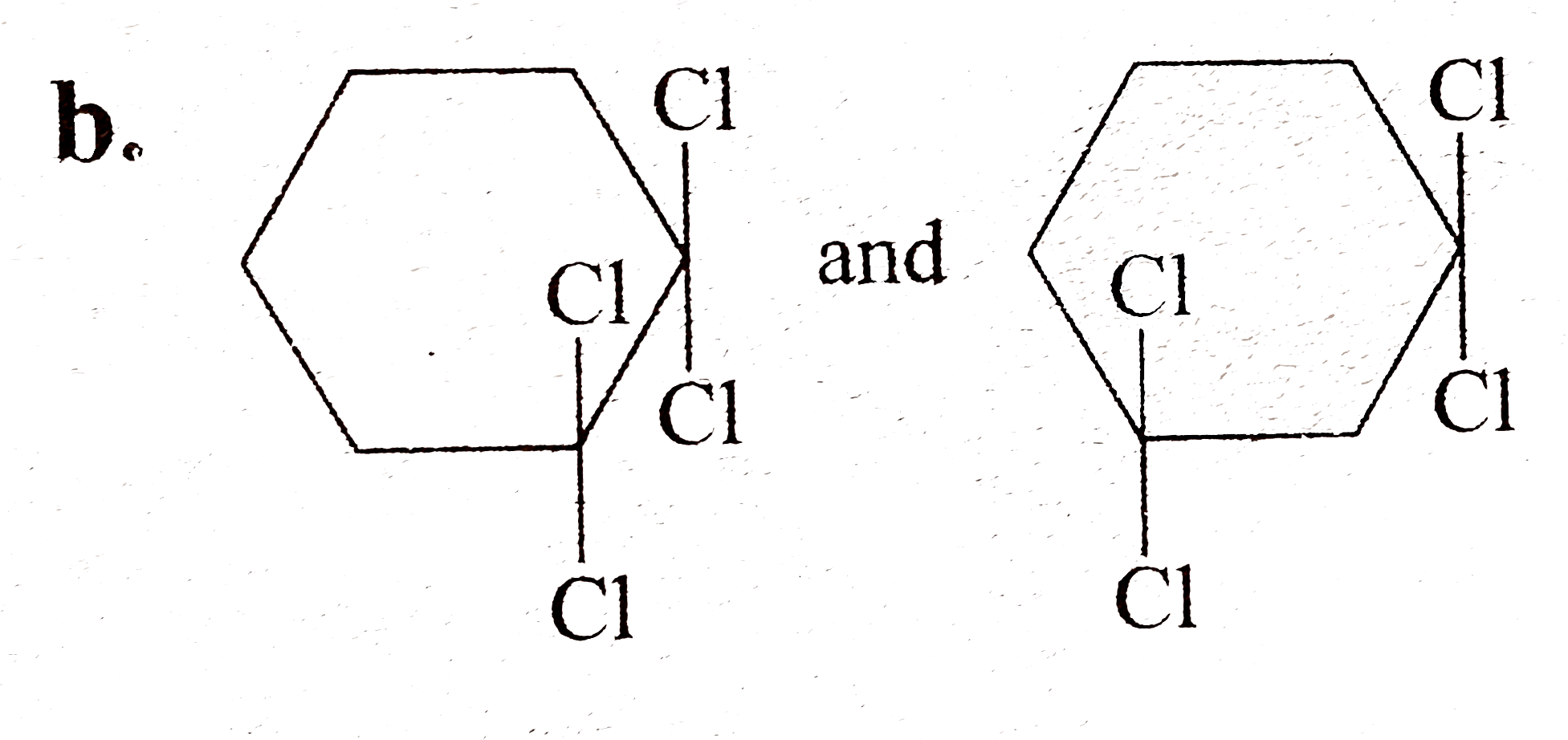
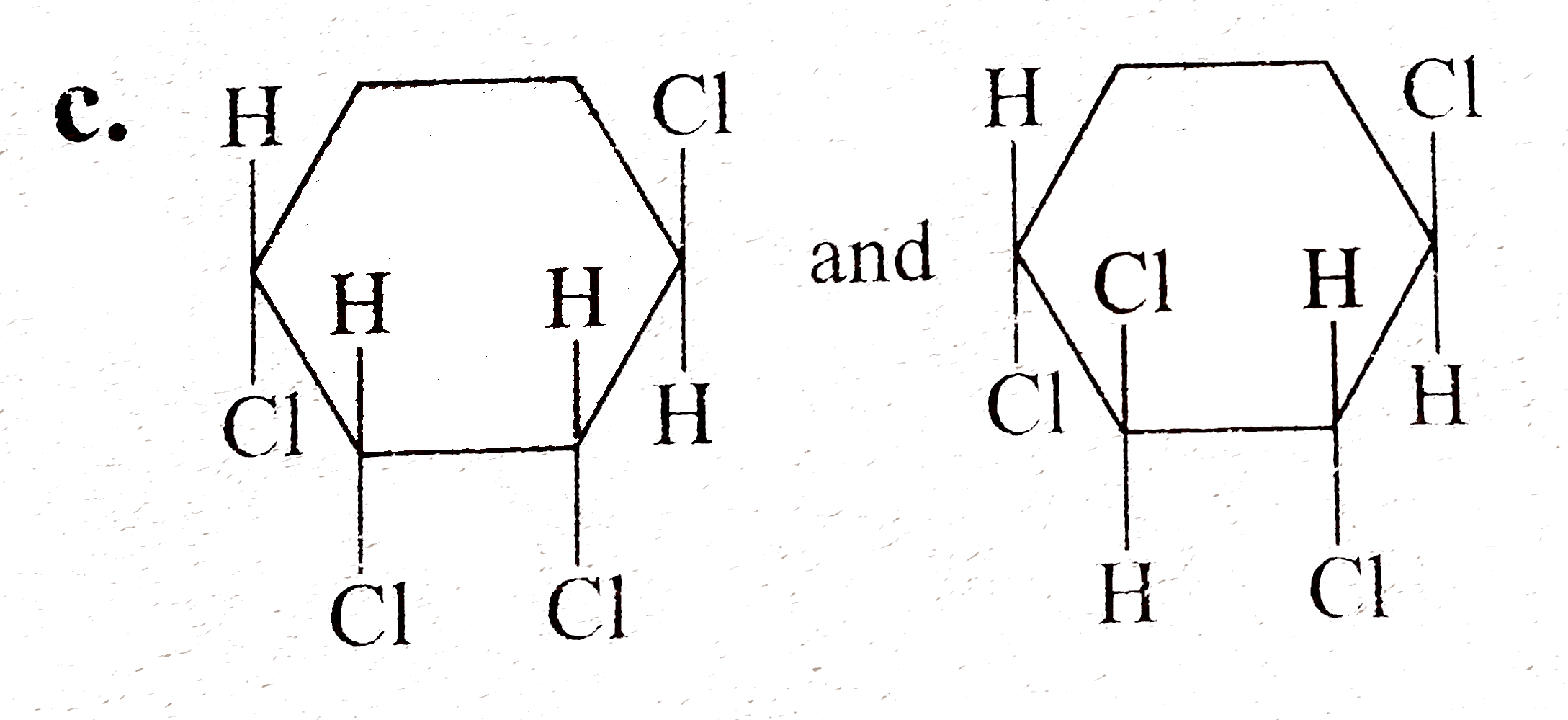

The correct Answer is:a
Anti − addition of Cl2.

Topper's Solved these Questions
- ALKENES AND ALKADIENESBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ALKENES AND ALKADIENESEXERCISE - Multiple Correct Answer Type
41 Videos
- ALKENES AND ALKADIENESBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ALKENES AND ALKADIENESEXERCISE - Single Correct Answer Type
62 Videos
- ALKENES AND ALKADIENESBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ALKENES AND ALKADIENESEXERCISE - EXERCISES
29 Videos
- ALKANES AND CYCLOALKANESBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ALKANES AND CYCLOALKANESEXERCISE - Archives
13 Videos
- ALKYNESBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ALKYNESEXERCISE - Exercises (Archives - Analytical and Desriptive Type)
4 Videos
Similar Questions
If EandFare the complementary events of events EandF, respectively, and if P(F) ∈ [0,1]
View SolutionThe three compounds (A),(B),and (C) on hydrogenation with H2+Pd give (D),(E) and (F), respectively.
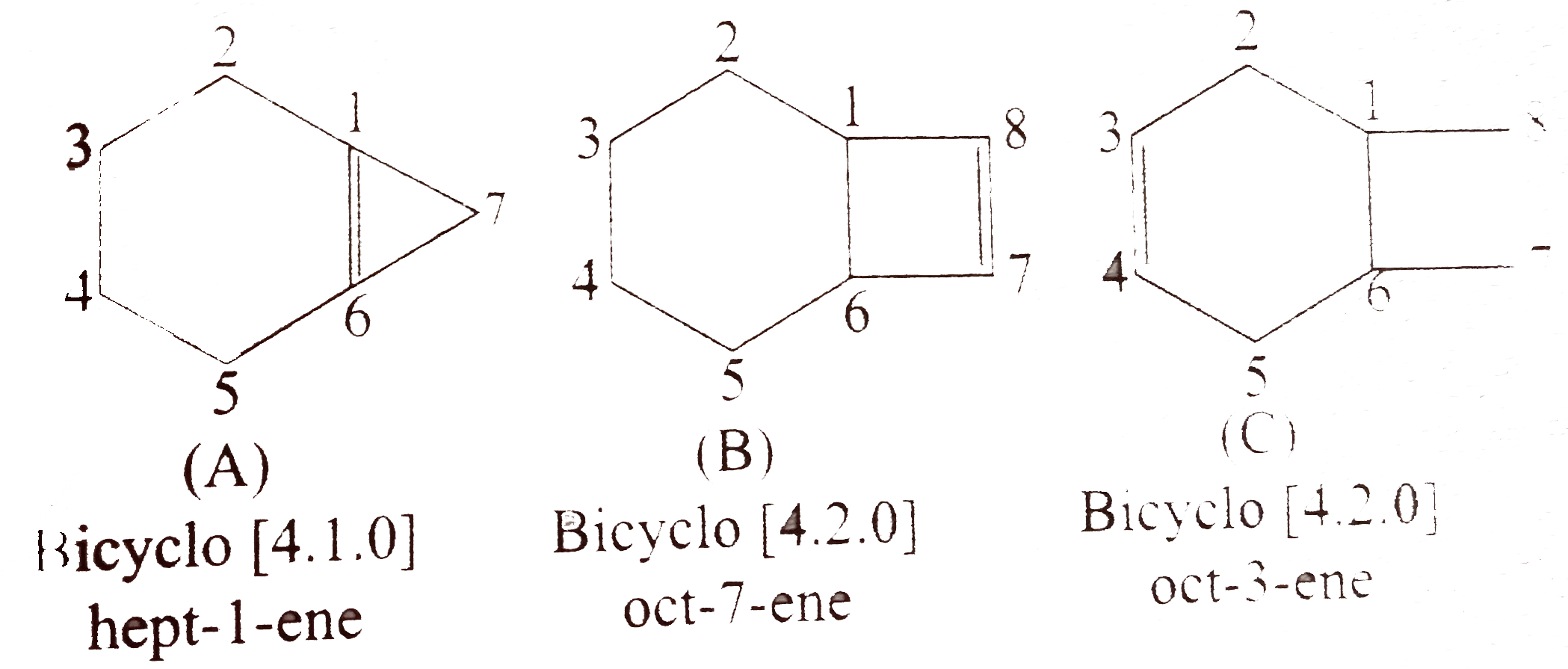
Compounds (D),(E) and (F) are :
View SolutionIncircle of ΔABC touches the sides BC, AC and AB at D, E and F, respectively. Then answer the following question
∠DEF is equal to
View SolutionXY is a line parallel to side BC of a triangle ABC. If BE∣∣AC and CF ∣∣ AB meet XY at E and F respectively, show that ar (ABE) = ar (ACF)
View SolutionABCD is a parallelogram. The sides AB and AD are produced to E and F respectively, such that AB = BE and AD = DF. Prove that : ΔBEC≅ΔDCF.
View SolutionIncircle of ΔABC touches the sides BC, AC and AB at D, E and F, respectively. Then answer the following question
The length of side EF is
View SolutionABCD is a quadrilateral in which AB=AD . The bisector of BAC and CAD intersect the sides BC and CD at the points E and F respectively. Prove that EF||BD.
View SolutionBisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are 90∘−12A,90∘−12B and 90∘−12C
View SolutionIn ABC, the three bisectors of the angle A, B and C are extended to intersect the circumcircle at D,E and F respectively. Prove that ADcosA2+BEcosB2+CFcosC2=2R(sinA+sinB+sinC)
View SolutionAD is a median of ΔABC . The bisector of ∠ADB and ∠ADC meet AB and AC in E and F respectively. Prove that EF||BC
View Solution
