This question has Statement I and Statement II. Of the four choices given after the Statement,choose the one that best describe the two Statements.
Statement-I: Component of →A along →B is equal to component of →B along →A.
Statement-II : Component of →A along →B is A cosθ where θ is the angle between two vectors.
Statement-I is true,Statement-II is true,Statement-II is a correct explanation of Statement-I
Statement-I is true,Statement-II is true,Statement-II is not a correct explanation of Statement-I
Statement-I is true,Statement-II is false.
Statement-I is false,Statement-II is true
The correct Answer is:D
Topper's Solved these Questions
Similar Questions
Knowledge Check
The component of →A along →B is √3 times that of the component of →B along →A. Then A:B is
A1:√3B√3:1C2:√3D√3:2Select the statement about two vector →A and →B .
AMax value of ∣∣→A+→B∣∣ = max value of ∣∣→A−→B∣∣BMax value of ∣∣→A+→B∣∣ = max value of ∣∣→A−→B∣∣CMax value of ∣∣→A+→B∣∣< max value of ∣∣→A−→B∣∣DInsufficient information provided.→A and →B are two vectors gives by →A=2ˆi+3ˆjand→B=ˆi+ˆj. The magnetiude of the component of →A along →B is :
A5√5B3√2C7√2D1√2
If →aand→b are the two vectors →R resultant of →a,→b as shown.
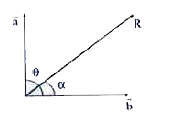
List-IList-IIA: component of→aalong→b(1)a2+b3B: component of→balong→a(2)0C: component of R along→a(3)RsinαD: component of R along→a(R)Rcosα
View SolutionStatement 1 : If |→a|=3,∣∣→b∣∣=4and∣∣→a+→b∣∣=5, then ∣∣→a−→b∣∣=5.
Statement 2 : The length of the diagonals of a rectangle is the same.
View SolutionTwo vectors →A and →B have equal magnitudes. If magnitude of →A+→B is equal to n times the magnitude of →A−→B, then the angle between →A and →B is :-
View SolutionStatement 1 : If |→a|=3,∣∣→b∣∣=4and∣∣→a+→b∣∣=5, then ∣∣→a−→b∣∣=5.
Statement 2 : The length of the diagonals of a rectangle is the same.
View SolutionWhich of the following statement about the sum of the two vectors →A and →B, is/are correct ?
View Solution
