If →aand→b are the two vectors →R resultant of →a,→b as shown.
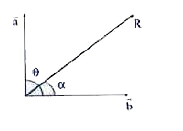
List-IList-IIA: component of→aalong→b(1)a2+b3B: component of→balong→a(2)0C: component of R along→a(3)RsinαD: component of R along→a(R)Rcosα
a-1, b-2, c-3, d-4
a-2,b-2,c-3,d-4
c-2,d-4,a-2,d-2
a-2,b-1, c-4, d-3
The correct Answer is:B
Step by step video & image solution for If veca and vecb are the two vectors vecR resultant of veca, vecb as shown. {:("List-I", "List-II"),("A: component of" veca "along" vecb,(1) a^(2)+b^(3)),("B: component of" vecb "along" veca,(2)0),("C: component of R along" veca,(3) R sin alpha),("D: component of R along" veca,(R) R cos alpha):} by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-IB (Vectors and Scalars)
5 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-IB (Addition and subtraction of vectors)
10 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-A (Ascending & descending Order)
2 Videos
- MAGNETISMBOOK - AAKASH SERIESCHAPTER - MAGNETISMEXERCISE - ADDITIONAL EXERCISE
22 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
Similar Questions
If →aand→b are non - zero vectors such that ∣∣→a+→b∣∣=∣∣→a−2→b∣∣ then
View SolutionIf →a=4ˆi+6ˆjand→b=3ˆi+4ˆk find the vector component of →a along →b.
View SolutionIf →a=4ˆi+6ˆjand→b=3ˆi+4ˆk find the vector component of →a alond →b.
View SolutionIf →A+→B=→R and 2→A+→B s perpendicular to →B then
View SolutionIf →aand→b are two vectors, such that ∣∣→a×→b∣∣=2 , then find the value of [→a→b→a]×→b .
View SolutionFind ∣∣→a−→b∣∣, if two vectors →aand→b are such that |→a|=2,∣∣→b∣∣=3and→a.→b=4.
View SolutionFind ∣∣→a−→b∣∣, if two vector →a and →b are such that |→a|=4,∣∣→b∣∣=5 and →a.→b=3
View SolutionIf →aand→b are two vectors , then prove that (→a×→b)2=∣∣∣→a.→a →a.→b→b.→a →b.→b∣∣∣
View SolutionIf →aand→b are two vectors , then prove that (→a×→b)2=∣∣∣→a.→a →a.→b→b.→a →b.→b∣∣∣
View SolutionIf →a,→b are unit vectors such that ∣∣→a+→b∣∣=1and∣∣→a−→b∣∣=√3, then |3→a+2→b |=
View Solution
