Two particles are simultaneously projected upwards from the top and bottom of a cliff of height H = 40 m. The speed of one is double that of the other and they meet after a time t = 2 second, find their speed of Projection.
We all know meeting time t=Hv2−v1
Where v2=2v1
therefore t=hv1 or v1=Ht=402=20msec
therefore v2=2v1=40msec.
Topper's Solved these Questions
Similar Questions
Two particles are simultaneously projected upwards from the top and bottom of a cliff of height = 20 m. If the speed of one is double that of the other and they meet after a time to 2 second, find their speed of projection.
View SolutionA stone is released from the top of a cliff .Another particles is simultaneously projected v=10msec from the bottom of the cliff if they meet after 2 second find the height of the cliff.
View Solution
Knowledge Check
A particle is dropped from rest from the top of a building of height 100m. At the same instant another particle is projected upward from the bottom of the building What should be the speed of projection of the particle projected from the bottom of building so that the particle cross each other after 1s? Acceleration due to gravity is 10 m/s2.
A100m/sB95m/sC90m/sD105m/sTwo projectiles are projected simultaneously from the top and bottom of a vertical tower of height h at angles 45∘ and 60∘ above horizontal respectively.Body strike at the same point on ground at distance 20m from the foot of the tower after same time.
The speed of projectile projected from the bottom isA40m/sB20√3m/sC40√3m/sD20√√3m/s
A ball is prouected vertical up from the top of a cliff of height h with a speed v1 Another ball is projected vertically up with a speed v2 from the bottom of the cliff, after a time t0 from the instantof projection of the first ball, When will the balls meet?.
View SolutionTwo particle of equal mass are projected simultaneously from the roof of a tower of height 20 m with same speed 20m//s, one horizontally and the other vertically upwards. Choose the correct alternative (s).
View SolutionTwo paarticles 1 and 2 are projected simultaneusly with velocities v1 and v2, respectively. Particle 1 is projectected vertically up from the top of a cliff of heitht h and particle 2 is projected vertically up from the bottom of the cliff. If the bodies meet (a) above the top of the cliff, (b) between the top and bottom of the the cliff, and (c ) below the bottom of the cliff, find the time of meeting of the particles.
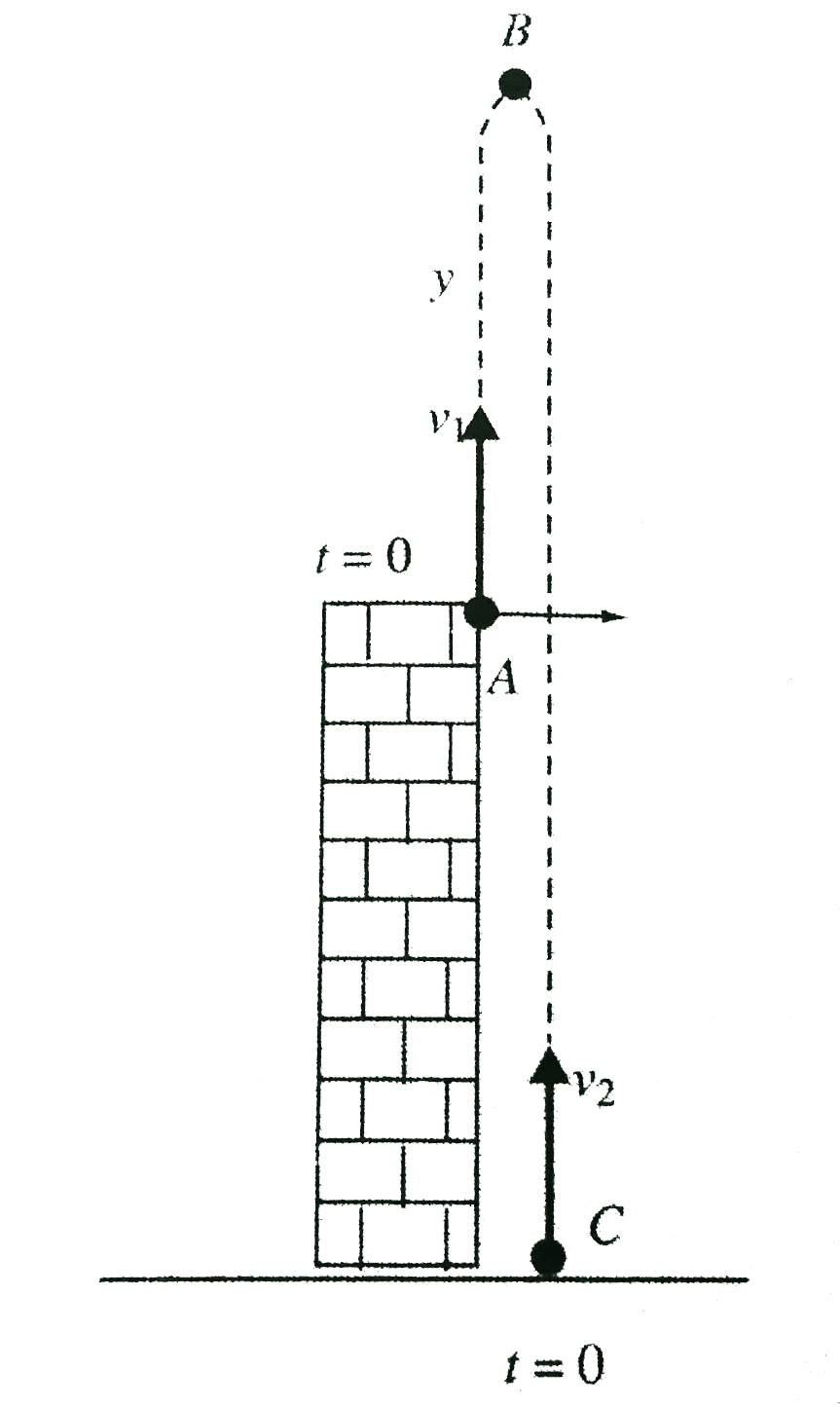 .
.
View SolutionTwo paarticles 1 and 2 are projected simultaneusly with velocities v1 and v2, respectively. Particle 1 is projectected vertically up from the top of a cliff of heitht h and particle 2 is projected vertically up from the bottom of the cliff. If the bodies meet (a) above the top of the cliff, (b) between the top and bottom of the the cliff, and (c ) below the bottom of the cliff, find the time of meeting of the particles.
 .
.
View SolutionTwo bodies 1 and 2 are projected simultaneously with velocities v1=2ms−1andv2=4ms−1 respectively. The body 1 is projected vertically up from the top of a cliff of height h = 10m and the body 2 is projected vertically up from the bottom of the cliff. If the bodies meet, find the time (in s) of meeting of the bodies.
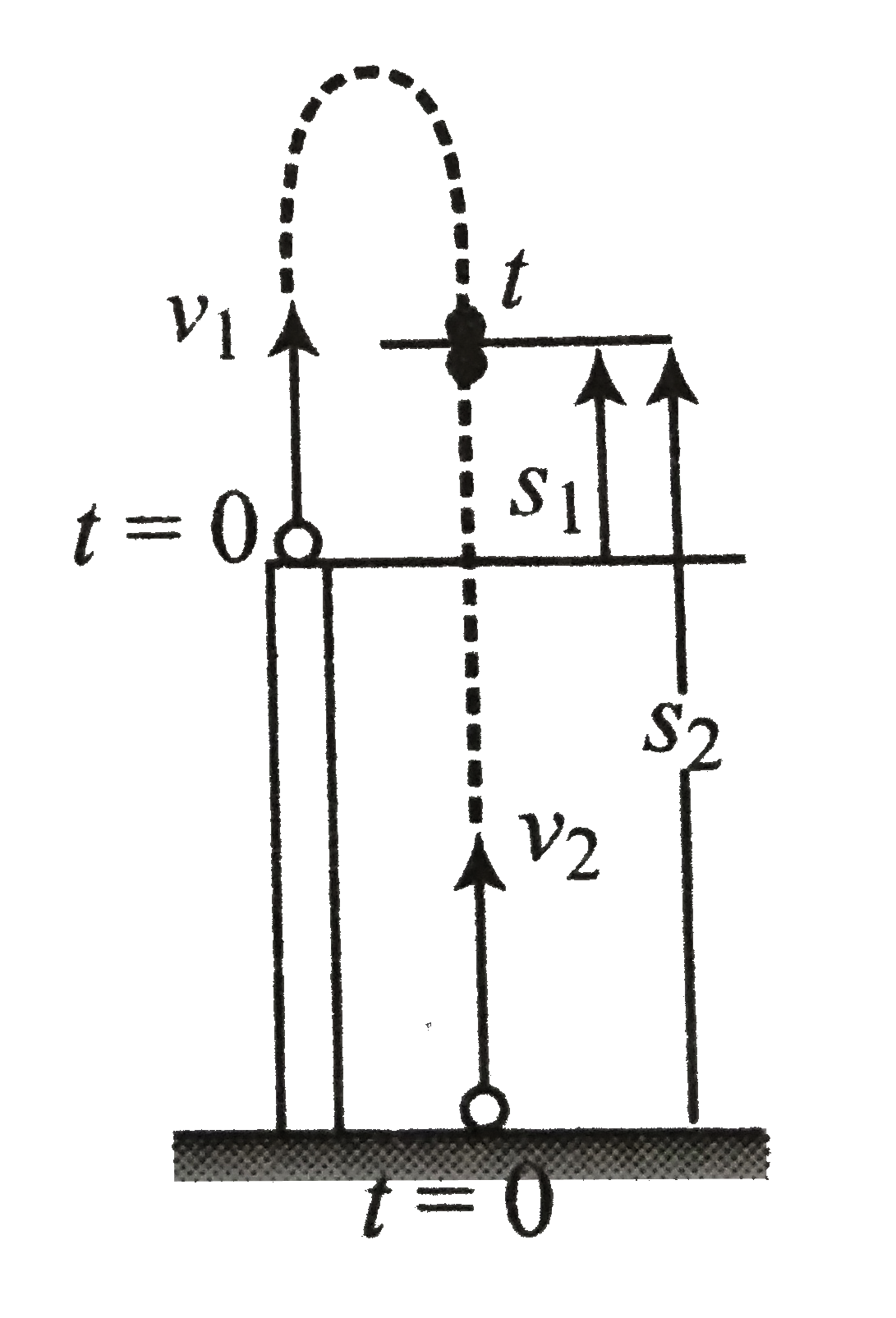
View SolutionTwo bodies 1 and 2 are projected simultaneously with velocities v1=2ms−1andv2=4ms−1 respectively. The body 1 is projected vertically up from the top of a cliff of height h = 10 and the body 2 is projected vertically up from the bottom of the cliff. If the bodies meet, find the time (in s) of meeting of the bodies.

View Solution
