Two particles are simultaneously projected upwards from the top and bottom of a cliff of height = 20 m. If the speed of one is double that of the other and they meet after a time to 2 second, find their speed of projection.
To solve the problem, we need to analyze the motion of two particles projected from the top and bottom of a cliff of height 20 meters. Let's denote the speed of the particle projected from the bottom as V and the speed of the particle projected from the top as 2V (since one speed is double the other).
1. Understanding the Motion:
- Let particle A be projected from the top of the cliff with speed 2V.
- Let particle B be projected from the bottom of the cliff with speed V.
- Both particles meet after t=2 seconds.
2. Distance Covered by Particle A:
- The distance covered by particle A in 2 seconds can be calculated using the second equation of motion:
hA=uAt−12gt2
where:
- uA=2V (initial speed of particle A)
- g=10m/s2 (acceleration due to gravity)
- t=2s
Plugging in the values:
hA=2V⋅2−12⋅10⋅(2)2
hA=4V−20
3. Distance Covered by Particle B:
- The distance covered by particle B in 2 seconds is:
hB=uBt−12gt2
where:
- uB=V (initial speed of particle B)
Plugging in the values:
hB=V⋅2−12⋅10⋅(2)2
hB=2V−20
4. Total Distance:
- Since the total height of the cliff is 20 meters, the distances covered by both particles must add up to the height of the cliff:
hA+hB=20
Substituting the expressions for hA and hB:
(4V−20)+(2V−20)=20
Simplifying this:
6V−40=20
6V=60
V=10m/s
5. Finding the Speeds:
- The speed of the particle projected from the bottom (B) is V=10m/s.
- The speed of the particle projected from the top (A) is 2V=20m/s.
Final Answer:
- The speed of projection for the particle from the bottom is 10m/s.
- The speed of projection for the particle from the top is 20m/s.
---
- Let particle A be projected from the top of the cliff with speed 2V.
- Let particle B be projected from the bottom of the cliff with speed V.
- Both particles meet after t=2 seconds.
- The distance covered by particle A in 2 seconds can be calculated using the second equation of motion:
hA=uAt−12gt2
where:
- uA=2V (initial speed of particle A)
- g=10m/s2 (acceleration due to gravity)
- t=2s
hA=2V⋅2−12⋅10⋅(2)2
hA=4V−20
- The distance covered by particle B in 2 seconds is:
hB=uBt−12gt2
where:
- uB=V (initial speed of particle B)
hB=V⋅2−12⋅10⋅(2)2
hB=2V−20
- Since the total height of the cliff is 20 meters, the distances covered by both particles must add up to the height of the cliff:
hA+hB=20
Substituting the expressions for hA and hB:
(4V−20)+(2V−20)=20
Simplifying this:
6V−40=20
6V=60
V=10m/s
- The speed of the particle projected from the bottom (B) is V=10m/s.
- The speed of the particle projected from the top (A) is 2V=20m/s.
- The speed of projection for the particle from the bottom is 10m/s.
- The speed of projection for the particle from the top is 20m/s.
Topper's Solved these Questions
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) LEVEL-II & III
15 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-I
45 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) LEVEL-I (True/False)
2 Videos
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS
1 Video
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION-III
2 Videos
Similar Questions
A stone is released from the top of a cliff .Another particles is simultaneously projected v=10msec from the bottom of the cliff if they meet after 2 second find the height of the cliff.
View SolutionA ball is prouected vertical up from the top of a cliff of height h with a speed v1 Another ball is projected vertically up with a speed v2 from the bottom of the cliff, after a time t0 from the instantof projection of the first ball, When will the balls meet?.
View Solution
Knowledge Check
A particle is dropped from rest from the top of a building of height 100m. At the same instant another particle is projected upward from the bottom of the building What should be the speed of projection of the particle projected from the bottom of building so that the particle cross each other after 1s? Acceleration due to gravity is 10 m/s2.
A100m/sB95m/sC90m/sD105m/sTwo particles are projected simultaneously from the level ground as shown figure. They may collide after a time :
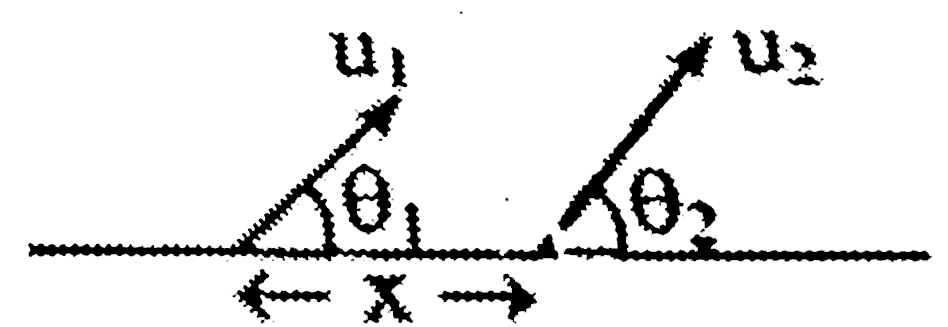 Axsinθ2u1Bxcosθ2u2Cxsinθ2u1sin(θ2−θ1)Dxsinθ1u2sin(θ2−θ1)
Axsinθ2u1Bxcosθ2u2Cxsinθ2u1sin(θ2−θ1)Dxsinθ1u2sin(θ2−θ1)Two projectiles are projected simultaneously from the top and bottom of a vertical tower of height h at angles 45∘ and 60∘ above horizontal respectively.Body strike at the same point on ground at distance 20m from the foot of the tower after same time.
The speed of projectile projected from the bottom isA40m/sB20√3m/sC40√3m/sD20√√3m/s
Two paarticles 1 and 2 are projected simultaneusly with velocities v1 and v2, respectively. Particle 1 is projectected vertically up from the top of a cliff of heitht h and particle 2 is projected vertically up from the bottom of the cliff. If the bodies meet (a) above the top of the cliff, (b) between the top and bottom of the the cliff, and (c ) below the bottom of the cliff, find the time of meeting of the particles.
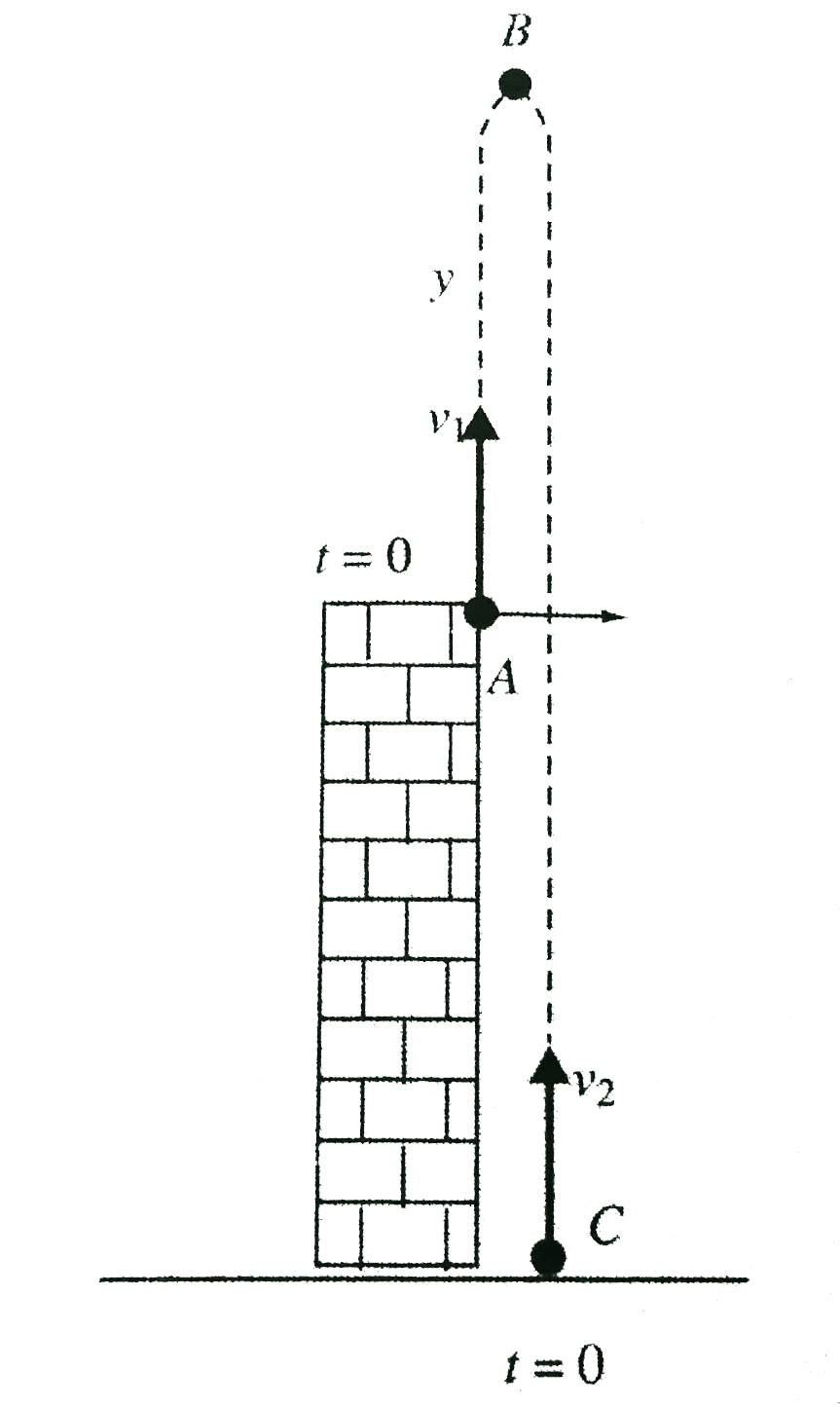 .
.
View SolutionA ball is projected downward from the top of a cliff of height h with an initial speed v.Another ball is simultaneously projected vertically up from the bottommost of the cliff with the same speed.When do they meet?
View SolutionTwo bodies 1 and 2 are projected simultaneously with velocities v1=2ms−1andv2=4ms−1 respectively. The body 1 is projected vertically up from the top of a cliff of height h = 10 and the body 2 is projected vertically up from the bottom of the cliff. If the bodies meet, find the time (in s) of meeting of the bodies.
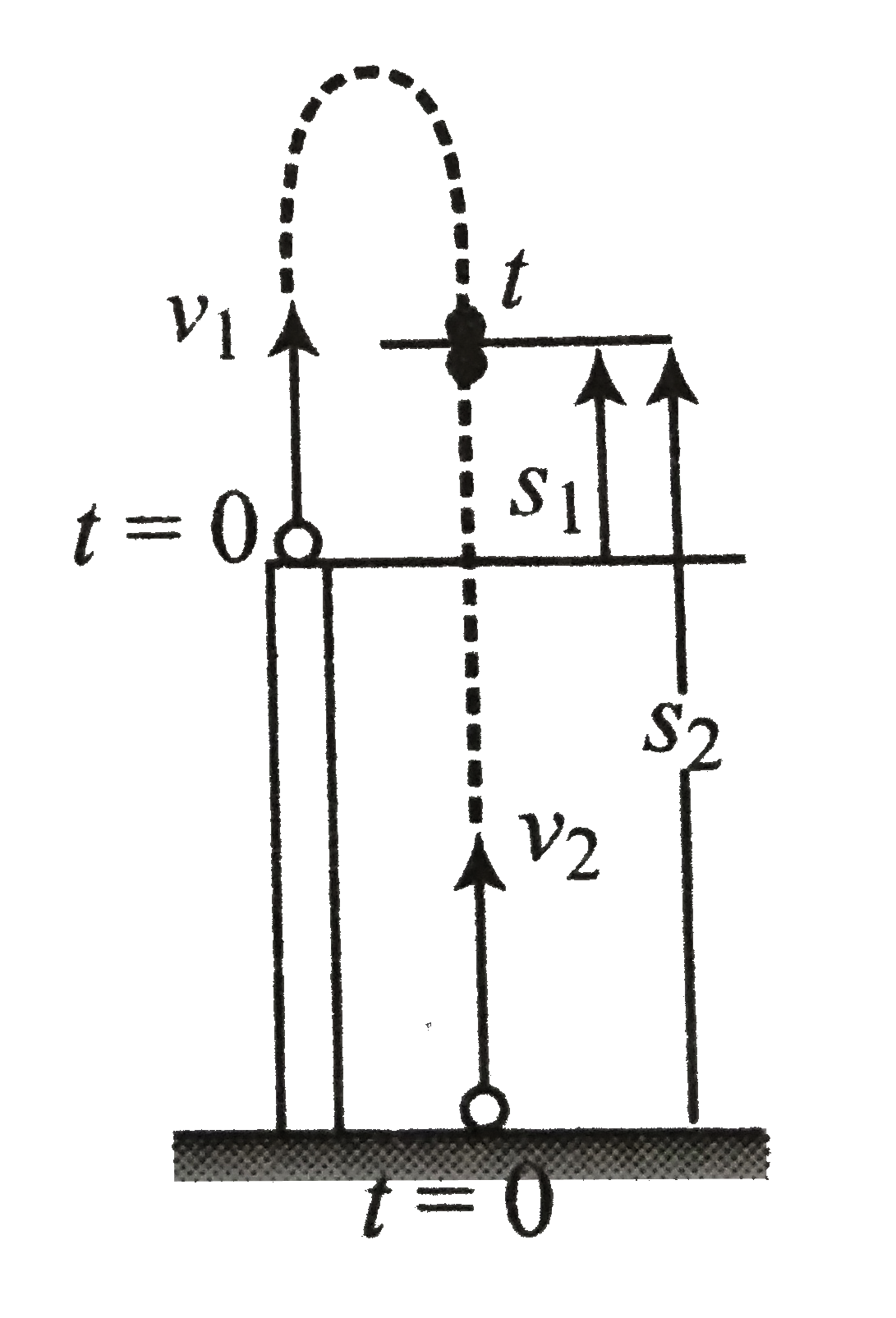
View SolutionTwo projectiles are projected simultaneously from the top and bottom of a vertical tower of height h at angles 45∘ and 60∘ above horizontal respectively.Body strike at the same point on ground at distance 20m from the foot of the tower after same time.
The ratio of the speed of the projectile projected from the top and the speed of the projectile projected from the bottom of tower is
View SolutionTwo projectiles are projected simultaneously from the top and bottom of a vertical tower of height h at angles 45∘ and 60∘ above horizontal respectively.Body strike at the same point on ground at distance 20m from the foot of the tower after same time.
The time of flight of projectles is
View Solution