A horizontal plane supports a stationary vertical cylinder of radius R and disc A attached to the cylinder by a horizontal thread AB of length l. An initial velocity is imparted to the disc as shown in figure . How long will it move along the plane till it strikes the cylinder? The friction is assumed to be absent.
Topper's Solved these Questions
Similar Questions
A horizontal plane supports a stationary vertical cylinder of radius R and a disc A attached to the cylinder by a horizontal thread AB of length l0 (figure, to view). An initial velocity v0
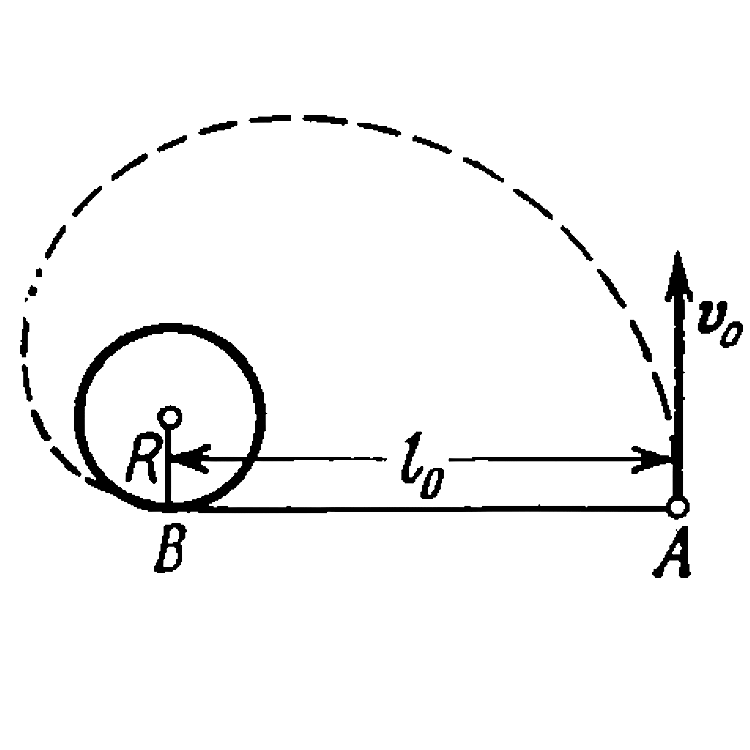
is imparted to the disc as shown in the figure. How long will it move along the plane until it strikes against the cylinder? The friction is assumed to be absent.
View SolutionA horizontal plane supports a fixed vertical cylinder of radius R and a particle is attached to the cylinder by a horizontal thread AB as shown in Fig. The particle initially rest on a horizontal plane. A horizontal velocity v0 is imparted to the particle, normal to the threading during subsequent motion. Point out the false statements:
View Solution
Knowledge Check
A horizontal plane supports a fixed vertical cylinder of radius R and a particle is attached to the cylinder by a horizontal thread AB as shown in Fig. The particle initially rest on a horizontal plane. A horizontal velocity v0 is imparted to the particle, normal to the threading during subsequent motion. Point out the false statements:
AAngular momentum of particle about O remains constant.BAngular momentum about B remains constantCMomentum and kinetic energy both remain constant.DKinetic energy remains constantA cylinder is rolling towards a cube of same mass on rough horizontal surface ( coefficient of friction = μ) with velocity v0 as shown in figure. Assume elastic collision and friction is negligible between cube and cylinder. Then after collision
ACylinder will stop permanentlyBCylinder will stop and then move towards right.CThe maximum seperation between cylinder and block is 4v209μgDThe time after the collision , the cylinder will again start pure rolling is v03μg
On a horizontal smooth plane there is a fixed vertical cylinder and a particle A connected to the cylinder by a thread AB. The particle is set in motion with the initial velocity v as shown in the figure. Is there any fixed point relative to which the angular
momentum of the particle is constant in the process of motion?
View SolutionA cylinder of mass M and radius R is to be raised on a horizontal step of height h=R3. Cylinder is pulled by a rope as shown in figure. Assuming no slipping, the minimum value of force F to raise the cylinder is
_PHY_E05_246_Q01.png)
View SolutionA uniform solid cylinder of radius R=15cm rolls over a horizontal plane passing into an inclined plane forming an angle α=30∘ with the horizontal(figure). Find the maximum value of the velocity v0 which still permits the cylinder to roll onto the inclined plane section without a jump. The sliding is assumed to be absent.
View SolutionA disc of radius R is moving on a rough horizontal surface with velocity v and angular speed ω at an instant as shown in figure. Choose the correct statement.
View SolutionA disc of radius R is moving on a rough horizontal surface with velocity v and angular speed ω at an instant as shown in figure. Choose the correct statement.
View SolutionA cylinder is rolling towards a cube of same mass on rough horizontal surface ( coefficient of friction = μ) with velocity v0 as shown in figure. Assume elastic collision and friction is negligible between cube and cylinder. Then after collision
View Solution