The Young's modulus of iron and steel are 5×1010N/m2 and 2×1011N/m2 respectively. An iron wire and steel wire of same length are extended by 2 mm under the same force. If the radii of iron and steel wires are RI and RS respectively, then what will be the relation between RI and RS?Solution in Bengali
Step by step video & image solution for The Young's modulus of iron and steel are 5xx10^10N//m^2 and 2xx10^11N//m^2 respectively. An iron wire and steel wire of same length are extended by 2 mm under the same force. If the radii of iron and steel wires are R_I and R_S respectively, then what will be the relation between R_I and R_S? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A ball of mass 0.1 kg is suspended by a string 30 cm long. Keeping the string always taut, the ball describes a horizontal circle of radius 15 cm. Find its angular speed and tension.
View SolutionWhat is the ratio of SI units to C.G.S. unit of G?
View SolutionFind the increment in the length of a steel wire of length 5m and radius 6mm under its own weight. Density of steel =8000kg/m3 and young's modulus of steel =2×1011N/m2. What is the energy stored in the wire ? (Take g =9.8m/s2)
View SolutionYoung's modulus of brass and steel are 10×1010N/m and 2×1011N/m2, respectively. A brass wire and a steel wire of the same length are extended by 1mm under the same force. The radii of the brass and steel wires are RB and RS. respectively. Then
View SolutionSteel and copper wires of same length are stretched by the same weight one after the other. Young's modulus of steel and copper are 2xx10^(11)(N)/(m^2) and 1.2xx10^(11)(N)/(m^2) . The ratio of increase in length is
View SolutionThe young 's modulus of brass and steel are 1.0 xx 10^(11) Nm^(-2) and 2.0 xx 10^(11) N//m^(2) . Respectively . A brass wire and steel wire of the same length extend by 1 mm, each under the same forece . It radii of brass and steel wires are R_(B) and R_(S) respectively, them
View SolutionThe Young's modulus of brass and steel are respectively 1.0×1011N/m2 and 2.0×1011N/m2 . A brass wire and steel wire of the same length are extended by 1mm each under the same force. If radii of brass and steel wires are RB and RS respectively,. then
View SolutionThe Young's modulus of brass and steel are respectively 1.0×1011Nm−2 and 2.0×1011Nm−2. A brass wire and a steel wire of the same length are extended by 1 mm each under the same force. If radii of bras and steel wires are RB and Rs respectively, then
View SolutionA steel wire of length 2.5 m and area of cross section 1.25mm2, when it is stretched by a force of 40 N and Y for steel is 2×1011N/m2. The extension produced in a steel wire is
View SolutionA steel wire of length 5 m and area of cross-section 4mm2 is stretched by 2 mm by the application of a force. If young's modulus of steel is 2×1011N/m2, then the energy stored in the wire is
View SolutionThe Young's modulii of brass ans steel are in the ratio of 1:2. A brass wire and a steel wire of the same length are extended by the same amount under the same deforming force. If rB and rS are the radii of brass and steel wires respectively, then
View SolutionAn iron wire of length 4 m and diameter 2 mm is loaded with a weight of 8 kg. if the Young's modulus Y for iron is 2×1011N/m2 then the increase in the length of the wire is
View SolutionIf the ratio of lengths, radii and Young's modulus of steel and brass wires shown in the figure are a, b and c respectively, the ratio between the increase in lengths of brass and steel wires would be Brass and steel wire would be
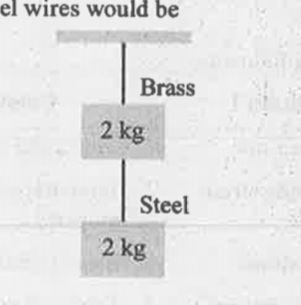
View Solutionपीतल व स्टील के यंग प्रत्यास्थता गुणांक 1.0×1010न्यूटन/मी2 व 2×1010न्यूटन/मी2 है। यह पीतल व एक स्टील के तारों पर (समान लम्बाई) समान बल लगाने पर, 1 मिमी खिंच जाते हैं। पीतल व स्टील के तारों की त्रिज्याएं RB व RS है तो
View SolutionThe Young's modulus of brass and steel are 10 ^(11) Nm ^(-2) and 2 xx 10 ^(11) Nm ^(-2) respectively. A brass wire and a steel wire of the same length extend by 1 mm, each under the same force. If radii of brass and steel wires are R_(B) and R_(S) respectively, then .. .
View SolutionA steel wire of length 5 m and area of cross-section 4mm2 is stretched by 2 mm by the application of a force. If young's modulus of steel is 2×1011N/m2, then the energy stored in the wire is
View Solution
