A solid cone hangs from a frictionless pivot at the origin O, as shown. If ˆi,ˆj and ˆk are unit vectors, and a, b and c, are positive constants, which of the following forces F applied to the rim of the cone at a point P results in a torque τ on the cone with a negative component τZ?
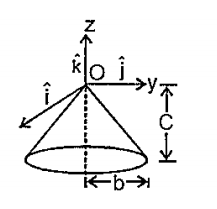
→F=aˆk, P is (0, b, -c)
→F=aˆk, P is (0, -b, -c)
→F=aˆj, P is (-b, 0 -c)
none of these
The correct Answer is:C
Topper's Solved these Questions
Similar Questions
A force →F=Aˆi+Bˆj is applied to a point whose radius vector relative to the origin is →r=aˆi+bˆj, where a, b, A,B are constants and ˆi, ˆj are unit vectors along the X and Y axes. Find the torque →τ and the arm l of the force →F relative to the point O.
View Solution(i) Find the torque of a force 7ˆi+3ˆj−5ˆk about the origin. The force acts on a particle whose position vector is ˆi−ˆj+ˆk.
(ii) Show that moment of a couple does not depend on the point about which you take the moments.
View Solution
Knowledge Check
A solid cone hanges from a frictionless pivot at the origin O, as shown. If ˆi,ˆj and ˆk are unit vectors, and a,b, and c are positive constants, which of the following forces F applied to the rim of the cone at a point P results in a torque τ on the cone with a negative component τZ ?
 .AF=aˆk,P is (0,b,−c)BF=−aˆk,P is (0,−b,−c)CF=aˆj,P is (−b,0,−c)DNone
.AF=aˆk,P is (0,b,−c)BF=−aˆk,P is (0,−b,−c)CF=aˆj,P is (−b,0,−c)DNoneA force F=Ai+Bj is applied to a point whose radius vector relative to the origin of coordinates O is equal to r=ai+bj, where a, b, A, B are constants, and i,j are the unit vectors of the x and y axes. Find the moment N and the arm l of the force F relative to the point O.
AaB−Ab√A2+B2BaA−Bb√A2+B2CaB+Ab√A2+B2DAb−aB√A2+B2
(i) Find the torque of a force 7ˆi+3ˆj−5ˆk about the origin. The force acts on a particle whose position vector is ˆi−ˆj+ˆk.
(ii) Show that moment of a couple does not depend on the point about which you take the moments.
View SolutionA round cone with half-angle α=30∘ and the radius of the base R=5.0cm rolls uniformly and without slipping over a horizontal plane as shown in fiugre. The cone apex is hinged at the point O which is one the same level with the point C, the cone base centre. The velocity of point C is v=10.0cm/s. Find the moduli of
(a) the vector of the angular velocity of the cone and the angle it forms with the vertical,
(b) the vector of the angular acceleration of the cone.

View SolutionIn Fig. 10-73, a particle of mass m is released from rest at point A, at distance b from the origin, and falls parallel to a vertical y axis. As a function of time t and with respect to the origin, find the magnitudes of (a) the torque τ on the particle due to the gravitational force and (b) the angular momentum L of the particle. ( c) From those results, verify that τ=dL/dt.

View SolutionThe position vector of a particle P with respect to a stationary point O change with time according to the law →r=→bsinωt+→ccosωt where →b and →c are constant vectors with bpotc and ω is a positive constant. Find the equation of the path of the particle y=f(x), assuming x an dy axes to coincide with the direction of the vector →b and →c respectively and to have the origin at the point O
View SolutionThe position vectors of points A and B w.r.t. the origin are →a=ˆi+3ˆj−2ˆkand→b=3ˆi+ˆj−2ˆk, respectively. Determine vector −−→OP which bisects angle AOB, where P is a point on AB.
View SolutionThe position vectors of points A and B w.r.t. the origin are →a=ˆi+3ˆj−2ˆkand→b=3ˆi+ˆj−2ˆk, respectively. Determine vector −−→OP which bisects angle AOB, where P is a point on AB.
View Solution
