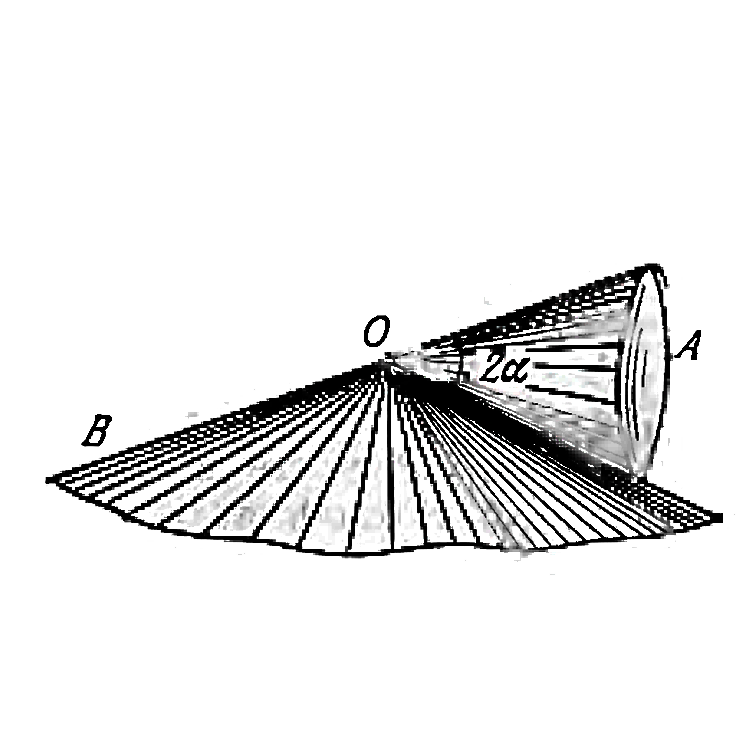
A round cone with half-angle α=30∘ and the radius of the base R=5.0cm rolls uniformly and without slipping over a horizontal plane as shown in fiugre. The cone apex is hinged at the point O which is one the same level with the point C, the cone base centre. The velocity of point C is v=10.0cm/s. Find the moduli of
(a) the vector of the angular velocity of the cone and the angle it forms with the vertical,
(b) the vector of the angular acceleration of the cone.

(a) Let the axis of the cone (OC) rotates in anticlockwise sense with constant angular velocity →ω and the cone itself about it's own axis (OC) in clockwise sense with angular velocity →ω0(figure). Then the resultant angular velocity of the cone.
→ω=→ω+→ω0 (1)
As the rolling is pure the magnitudes of the vectors →ω and →ω0 can be easily found from figure.
ω'=vRcotα, ω0=v/R (2)
As →ω⊥→ω0 from Eq. (1) and (2)
ω=√ω′2+ω20
√(vRcotα)2+(vR)2=vRcosα=2⋅3rad/s
(b) Vector of angular acceleration
→β=d→ωdt=d(→ω+→ω0)dt(as →ω= constant.)
The vector →ω0 which rotates about the OO′ axis with the angular velocity →ω, retains i magnitude. This increment in the time interval dt is equal to
|d→ω0|=ω0⋅ω′dt or in vector from d→ω0=(→ω×→ω0)dt.
Thus →β=→ω×→ω0
The magnitude of the vector →β is equal to
β=ω′ω0 (as →ω⊥→ω0)
So, β=vRcotαvR=v2R2tanα=2⋅3rad/s

Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - The Fundamental Equation Of Dynamics
59 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Laws Of Conservation Of Energy, Momentum And Angular Momentum
82 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena
38 Videos
Similar Questions
The volume of a cone is 18480cm3. If the height of the cone is 40cm. Find the radius of its base.
View SolutionA round cone A of mass m=3.2kg and half-angle α=10∘ rolls uniformly and without slipping along a round conical surface B so that its apex O remains stationary (figure). The centre of gravity of the cone A is at the same level as the point O and at a distance l=17cm from it. The cone's axis moves with angular velocity ω. Find:
(a) the static friction force acting on the cone A, if ω=1.0rad/s,
(b) at what values of ω the cone A will roll without sliding, if the coefficient of friction between the surfaces is equal to k=0.25.
View Solution
Knowledge Check
A solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.
AThe kinetic energy of rotation is 15mv20.BThe total kinetic energy is 710mv20.CThe mechanical energy (assume the ground as reference) is mgR+710mv20.DAll options are correct.A wheel is rolling uniformly along a level road without slipping . Velocity of the highest point on its rim about the road is V . Then magnitude of velocity of a point on its rim which is at the same level as that of the centre is
A√2VBV/2C2VDV/√2A cone was melted and cast into a cylinder of the same radius as that of the base of the cone. If the height of the cylinder is 5cm, find the height of the cone.
A15 cmB10 cmC18 cmD5 cm
A uniform solid cone of height 40 cm is shown in figure. The distance of centre of mass of the cone from point B (centre of the base) is :
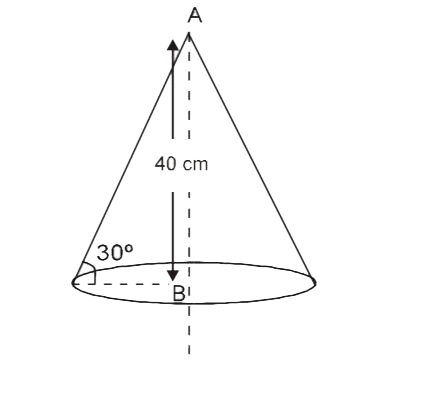
View SolutionA uniform solid cone of height 40 cm is shown in figure. The distance of centre of mass of the cone from point B (centre of the base) is :
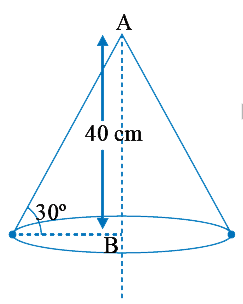
View SolutionA uniform solid cone of height 40 cm is shown in figure. The distance of centre of mass of the cone from point B (centre of the base) is :

View SolutionFind the volume of the cone of height 10 cm and radius of the base 3 cm.
View SolutionThe volume of a cone is 18480cm3. If the height of the cone is 40cm. Find the radius of its base.
View Solution
