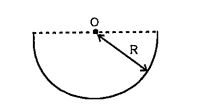
A current I flows in a long stright wire with its cross section having the form of a thin half ring of radius R.O is the centre of its mid section perpendicular to its length assume the wire extends to infinite length on either side of the mids ection then the magnetic field B at the centre O will be
B=μ0Iπr
B=(mu_0I)/(2piR)
B=μ0Iπ2R
B=μ0I2R
The correct Answer is:C
Topper's Solved these Questions
Similar Questions
A current I flows in a long straight wire with cross-section haviing the form of a thin half-ring of radius R (Fig). Find the induction of the magnitude field at the point O.

View SolutionA current I flows in a long straight wire whose cross section is in the shape of a thin quarter ring of radius R. Find the induction of the magnetic field (B) at point O on the axis.

View Solution
Knowledge Check
A current I flows an infinitely long wire with cross section in the form of a semi - circular ring of radius R. The magnitude of the magnetic induction along its axis is :
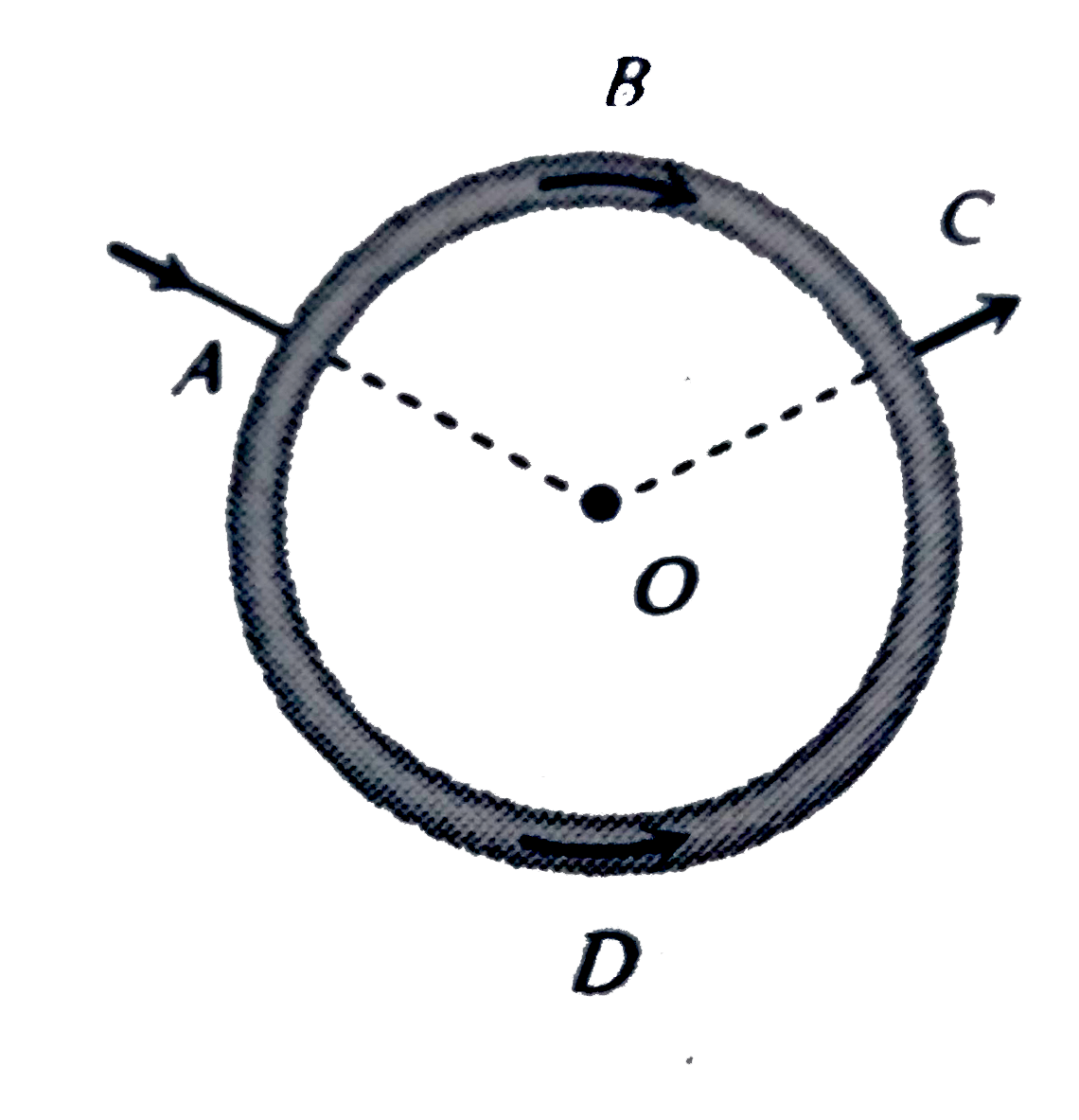
Aμ0I2π2RBμ0I2πRCμ0I4πRDμ0Iπ2RA current I flows along a thin wire shaped as shown in figure. The radius of the curved part of the wire is r. The field at the centre O of the coil is:
 Aμ04.irBμ02πrCμ0I2πrDμ0I8πr(3π+4)
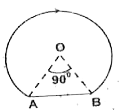
Aμ04.irBμ02πrCμ0I2πrDμ0I8πr(3π+4)A uniform wire is bent in the form of a circle of radius R. A current I enters at A and leaves at C as shown in the figure :
If the length ABC is half of the length ADC, the magnetic field at the centre O will be
 AZeroBμ0I2RCμ0I4RDμ0I6R
AZeroBμ0I2RCμ0I4RDμ0I6R
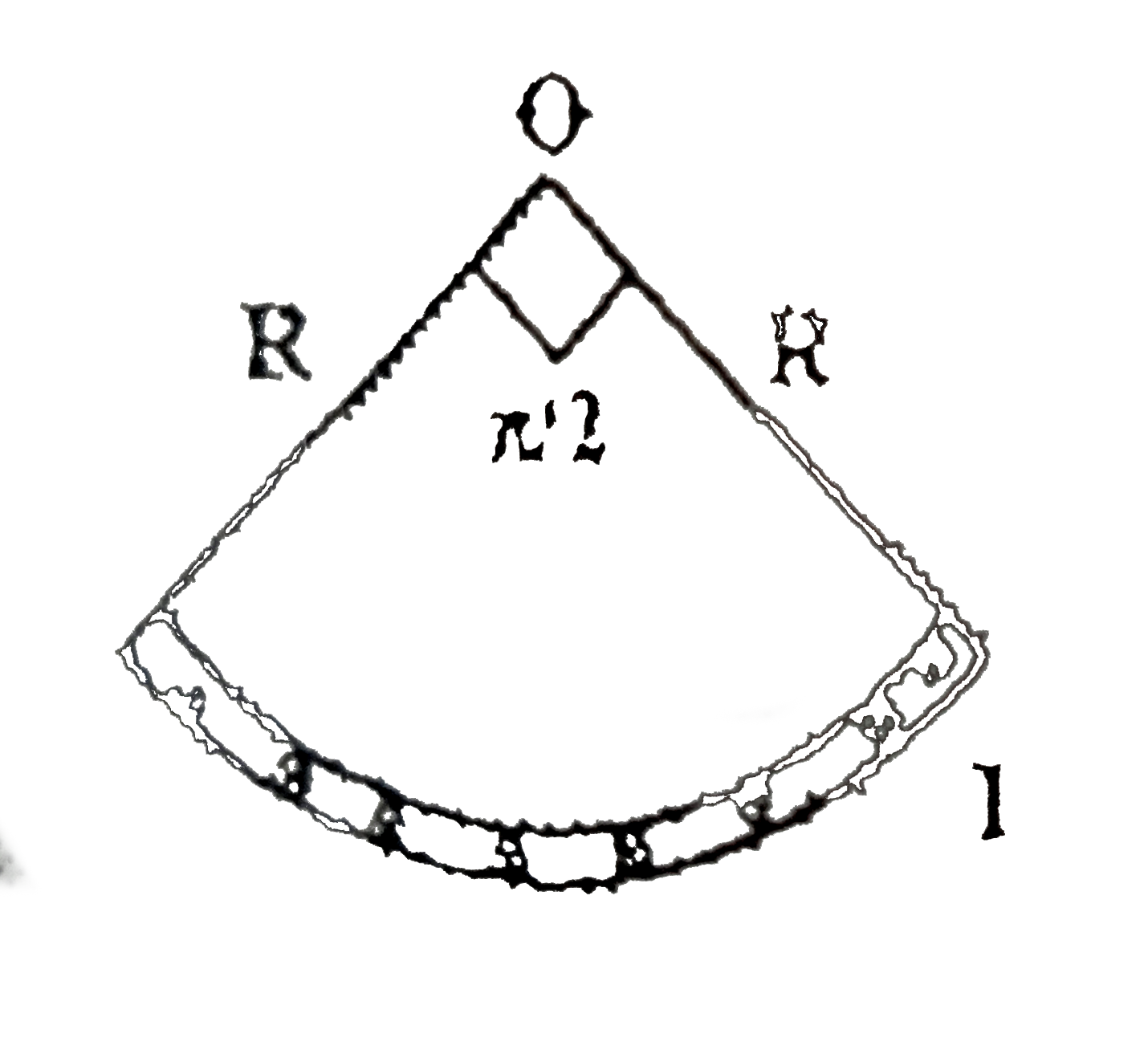
A current I flows in a long straight wire (into the plane of the paper) with cross-section having the from of a circular are of radius R a shown in the figure. Find the magnetic induction at the point O.
View SolutionA current I is flowing in a straight conductor of length L. The magnetic induction at a point distant L4 from its centre will be
View SolutionA current I flows along a thin wire shaped as shown in figure. The radius of the curved part of the wire is r. The field at the centre O of the coil is:

View SolutionA direct current I=10A flows in a long straight round conductor. Find the magnetic flux through a half of the wire's cross-section per one meter of its length.
View SolutionA rod having length L, density D and area of Cross-section A is rotating about the centre with velocity @ and perpendicular to its length. Its rotational kinetic energy is
View Solution
