A body enters in an MRI machine in 10s. If the magnctic field is 1.5T and circumference of the MRI mechine is 0.9m, then find out the magnitude of emf induced (in milli volt) in the body.
The correct Answer is:9.6
To find the magnitude of the induced EMF in the body entering the MRI machine, we can follow these steps:
Step 1: Understand the formula for induced EMF
The induced EMF (ε) can be calculated using Faraday's law of electromagnetic induction, which states:
ϵ=−dΦdt
where Φ is the magnetic flux.
Step 2: Calculate the change in magnetic flux
The magnetic flux Φ is given by:
Φ=B⋅A
where B is the magnetic field strength (in Tesla) and A is the area (in square meters) through which the magnetic field lines pass.
Step 3: Determine the area
Given the circumference of the MRI machine is C=0.9m, we can find the radius r using the formula for circumference:
C=2πr⟹r=C2π=0.92π
Now, calculate the area A:
A=πr2=π(0.92π)2=0.924π=0.814π
Step 4: Substitute values into the flux equation
Now we can substitute the values of B and A into the flux equation:
Φ=B⋅A=1.5⋅0.814π
Step 5: Calculate the change in flux over time
The change in flux over the time interval t=10s is:
ΔΦ=Φ−0=Φ
Thus, the induced EMF becomes:
ϵ=ΔΦt=1.5⋅0.814π10
Step 6: Simplify the expression
Calculating the above expression:
ϵ=1.5⋅0.8140π
Using π≈3.14:
ϵ=1.5⋅0.8140⋅3.14
Step 7: Calculate the numerical value
Calculating the numerator:
1.5⋅0.81=1.215
Calculating the denominator:
40⋅3.14=125.6
Now, divide:
ϵ=1.215125.6≈0.0097V
Step 8: Convert to millivolts
To convert volts to millivolts, multiply by 1000:
ϵ≈0.0097×1000≈9.7mV
Final Answer
The magnitude of the induced EMF in the body is approximately 9.7 mV.
---
The induced EMF (ε) can be calculated using Faraday's law of electromagnetic induction, which states:
ϵ=−dΦdt
where Φ is the magnetic flux.
The magnetic flux Φ is given by:
Φ=B⋅A
where B is the magnetic field strength (in Tesla) and A is the area (in square meters) through which the magnetic field lines pass.
Given the circumference of the MRI machine is C=0.9m, we can find the radius r using the formula for circumference:
C=2πr⟹r=C2π=0.92π
Now, calculate the area A:
A=πr2=π(0.92π)2=0.924π=0.814π
Now we can substitute the values of B and A into the flux equation:
Φ=B⋅A=1.5⋅0.814π
The change in flux over the time interval t=10s is:
ΔΦ=Φ−0=Φ
Thus, the induced EMF becomes:
ϵ=ΔΦt=1.5⋅0.814π10
Calculating the above expression:
ϵ=1.5⋅0.8140π
Using π≈3.14:
ϵ=1.5⋅0.8140⋅3.14
Calculating the numerator:
1.5⋅0.81=1.215
Calculating the denominator:
40⋅3.14=125.6
Now, divide:
ϵ=1.215125.6≈0.0097V
To convert volts to millivolts, multiply by 1000:
ϵ≈0.0097×1000≈9.7mV
The magnitude of the induced EMF in the body is approximately 9.7 mV.
Topper's Solved these Questions
Similar Questions
A body enters in an MRI machine in 10s. If the magnctic field is 1.5T and circumference of the MRI mechine is 0.9m, then find out the magnitude of emf induced (in milli volt) in the body.
View SolutionA flat, circular coil of radius 10cm has 100 turns of wire. Auniform magnetic field exists in a direction perpendicular to the plane of the coil. This ficld is increasing at the rate of 0.1Ts. Calculate the magnitude of emf induced (in volt) in the coil.
View Solution
Knowledge Check
If the current increases from zero to 1A in 0.1 s in a coil of 5 mH then magnitude of induced emf will be
A5 VB0.5 VC0.05 VD0.005 VThe inductance of a coil is 60μH. A current in this coil increase from 1.0A to 1.5A in 0.1 second. The magnitude of the induced e.m.f. is
A60×106(−60VB300×10−4VC30×10−4VD3×10−4VThe figure shows a uniform, 3.0 T magnetic field that is normal to the plane of a conducting, circular loop with a resistance of 1.5 Ω and a radius of 0.024 m. The magnetic field is directed out of the paper as shown . Note: The area of the non-circular portion of the wire is considered negligible compared to that of the circular loop.
If the magnetic field is held constant at 3.0 T and the loop is pulled out of the region that contains the field in 0.2 s, what is the magnitude of the average induced emf in the loop?A2.7×10−2VB6.4×10−2VC9.8×10−2VD5.4×10−2V
A square loop of side 20 cm and resistance 0.30 Ω is placed in a magnetic field of 0.4 T. The magnetic field is at an angle of 45∘ to the plane of loop. If the magnetic field is reduced to zero in 0.5 s, then find the induced emf and induced current in the loop in this time interval.
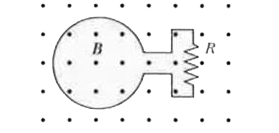
View SolutionIn the given arrangement magnetic field is B = 1T and radius of circular loop is 1m. Find emf induced in 1s.
View SolutionA force acts for 10 s on a body of mass 10 kg after which the force ceases and the body describes 50 m in the next 5 s. Find the magnitude of the force.
View SolutionA wire is moving with velocity 12×10−2m/s in a magnetic field of 0.5 T. if the induced emf is 9 mV, the length of wire is
View SolutionThe megnetic flux through a coil is 5×10−4 Wb. At time t=0. it reduces to ten percent of its original value in 0.5 s. The magnitude of e.m.f. induced in the coil is
View Solution
