Light of wavelength from a small He-Ne laser source is used in the school laboratory to shine on perfectly absorbing surface of a spacecraft of mass . The tịne needed' for the spacecraft to reachi a velocity of from rest is given by in scientific notation. Find the value of .
The correct Answer is:5
To solve the problem step by step, we will follow the reasoning provided in the video transcript and apply the relevant physics concepts.
Step 1: Determine the number of photons emitted per second by the laser.
The power of the laser is given as P=0.5mW=0.5×10−3W.
The energy of a single photon can be expressed as:
E=hν=hcλ
where h is Planck's constant (6.626×10−34Js), c is the speed of light (3×108m/s), and λ is the wavelength of the light.
The number of photons emitted per second, n, can be calculated using the formula:
P=n⋅E⟹n=PE=Pλhc
Substituting the values, we have:
n=0.5×10−3⋅λ6.626×10−34⋅3×108
Step 2: Calculate the rate of change of momentum.
The momentum of a single photon is given by:
p=Ec=hcλc=hλ
The rate of change of momentum (force) due to n photons is:
F=n⋅p=n⋅hλ
Substituting the expression for n:
F=(0.5×10−3⋅λ6.626×10−34⋅3×108)⋅hλ=0.5×10−3⋅6.626×10−346.626×10−34⋅3×108=0.5×10−33×108
Step 3: Relate force to acceleration.
Using Newton's second law, F=ma, where m=1000kg:
a=Fm=0.5×10−33×108⋅1000
Calculating a:
a=0.5×10−33×1011=16×1011m/s2
Step 4: Calculate the time to reach a velocity of 1km/s.
Using the first equation of motion v=u+at (where u=0):
t=va=100016×1011=1000⋅6×1011=6×1014s
Step 5: Express time in scientific notation.
The time t can be expressed as:
t=6×1014s
Here, α=6 and β=14.
Step 6: Calculate β−2α.
β−2α=14−2⋅6=14−12=2
Final Answer:
The value of β−2α is 2.
---
The power of the laser is given as P=0.5mW=0.5×10−3W.
E=hν=hcλ
where h is Planck's constant (6.626×10−34Js), c is the speed of light (3×108m/s), and λ is the wavelength of the light.
P=n⋅E⟹n=PE=Pλhc
Substituting the values, we have:
n=0.5×10−3⋅λ6.626×10−34⋅3×108
The momentum of a single photon is given by:
p=Ec=hcλc=hλ
The rate of change of momentum (force) due to n photons is:
F=n⋅p=n⋅hλ
Substituting the expression for n:
F=(0.5×10−3⋅λ6.626×10−34⋅3×108)⋅hλ=0.5×10−3⋅6.626×10−346.626×10−34⋅3×108=0.5×10−33×108
Using Newton's second law, F=ma, where m=1000kg:
a=Fm=0.5×10−33×108⋅1000
Calculating a:
a=0.5×10−33×1011=16×1011m/s2
Using the first equation of motion v=u+at (where u=0):
t=va=100016×1011=1000⋅6×1011=6×1014s
The time t can be expressed as:
t=6×1014s
Here, α=6 and β=14.
β−2α=14−2⋅6=14−12=2
The value of β−2α is 2.
Topper's Solved these Questions
Similar Questions
_S01_033_Q01.png)
In a typical young's double slit experiment a point source of monochromatic light is kept as shown in the figure. If the source is given an instantaneous velocity v=1 mm per second towards the screen, then the instantaneous velocity of central maxima is given as α×10−βcm/s upward in scientific notation find the value of α+β
View SolutionThe internal energy of monatomic ideal gas is 1.5(MR)T. One mole of helium is kept in a cylinder of cross-section 8.5cm2. The cylinder is closed by a light frictionless piston. The gas is heated slowly in a process during which a total of 42J heat is given to the gas. The temperature of the gas rises by 2C. The distance moved by the piston is given as α×10β meter. Find the value of (α+β). [Take universal gas constant R=253Jmol−1K−1. atmospheric pressure =100(kPa)]
View Solution
Knowledge Check
Light of wavelength λ from a small 0.5 mW He-Ne laser source, used in the school laboratory, shines from a spacecraft of mass 1000 kg. Estimate the time needed for the spacecraft to reach a velocity of 1.0km−1 from rest. The momentum p of a photon of wavelength λ is given by p=hλ, where h is Planck's constant.
A6..1018B3×1017C6×1017D2×1015
A horizontal cylindrical tank is half full of water ( refractive index =43) . The space above the water is filled with a light liquid of unknown refractive index (μ). A small laser source (s) can move along the curved bottom of the cylinder and aims a light beam towards the centre of the cylinder. The time needed by the laser beam to travel from the source to the rim of the cylinder depends on position (θ) of the source as shown in the graph. Find μ, it is given that sinθ0=56.
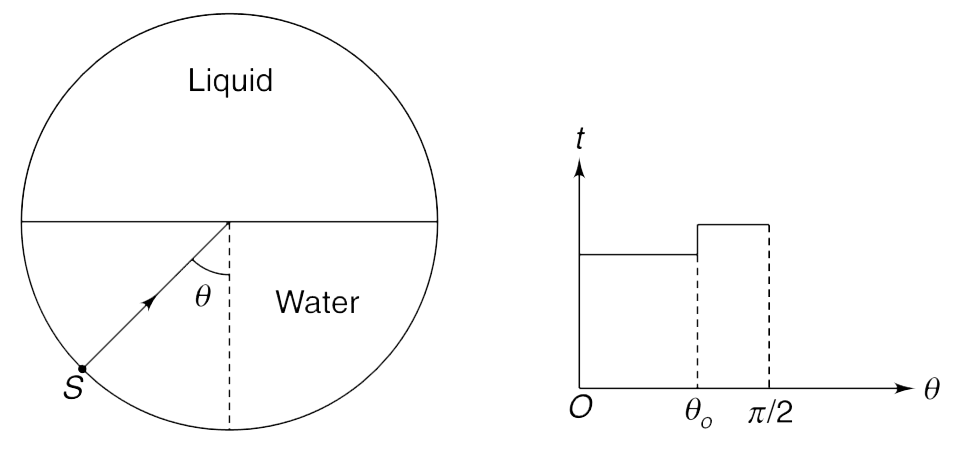
View Solution(a) A parallel beam of monochromatic light of wavelength 500 nm is incident normally on a perfectly absorbing surface. The power through any cross section of the beam is 10 W. Find
(i) the number of photons absorbed per second by the surface and
the force exerted by the lilght beam on the surface.
(a) Radiation of wavelength 200 nm, propagating in the form of a parallel beam, fall normally on a plane metallic surface. The intensity of the beam is 5 mW and its cross-sectional area is 1.0mm2. Find the pressure exerted by the radiation on the metallic surface if the radiation is completeley reflected.
(c) A parallel beam of monochromatic light of wavelength 663 nm is incident on a totally reflecting plane mirror. The angle of incidence is 60∘ and the number of photons striking the mirror per second is 1.0×1019 . Calculate the force exerted by the light beam on the mirror.
(d) A beam of white light is incident normally on a plane surface absorbing 70%) of the light and reflecting the rest. If the incident beam carries 10 W of power, find the force exerted by it on the surface.
View SolutionA projectile is to be launched from the surface of the earth so as to escape the solar system. Consider the gravitational force on the projectile due to the earth and the sun nly. The projectile is projected perpendicular to the radius vector of the earth relative to the centre of the sun in the direction of motion of the earth. Find the minimum speed of projection relative to the earth so that the projectile escapes out of the solar system. Neglect rotation of the earth. mass if the sum Ms2×1030kg, Mass of the earth Me=6.4×1024kg Radius if the earthRe=6.4×106m, Earth- Sun distence r=1.5×1011m
View SolutionTwo unequal masses of 1kg and 2kg are connected by a string going over a clamed light smooth pulley as shown in figure . The system is released from rest .The larger mass is stopped for a moment 1.0s after the system is set in motion.Find the time elapsed before the string is tight again.

View Solution(i) A source of sound emits waves of frequency f0=1200Hz. The source is travelling at a speed of v1=30m/s towards east. There is a large reflecting surface in front of the source which is travelling at a velocity of v2=60m/s towards west. Speed of sound in air is v=330m/s.
(a) Find the number of waves arriving per second at the reflecting surface.
(b) Find the ratio of wavelength (λ1) of sound in front of the source travelling towards the reflecting surface to the wavelength (λ2) of sound in front of the source approaching it after getting reflected.
(ii) A sound source (S) and an observer (A) are moving towards a point O along two straight lines making an angle of 60∘ with each other. The velocities of S and A are 18ms–1 and 12ms–1 respectively and remain constant with time. Frequency of the source is 1000Hz and speed of sound is v=330ms–1.
(a) Find the frequency received by the observer when both the source and observer are at a distance of 180 m from point O (see figure). (b) Find the frequency received by the observer when she reaches point O.
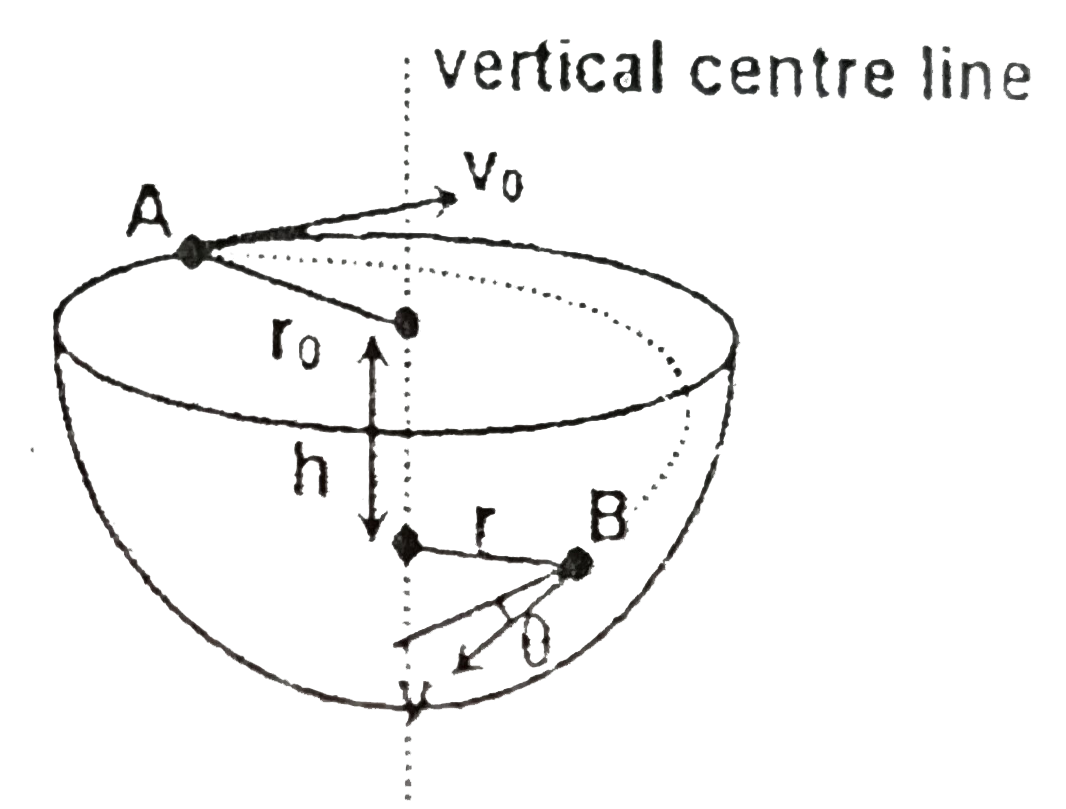
View SolutionA small particle is given an initial velocity v0=10m/s along the tangent to the brim of a fixed smooth hemisphere bowl of radius r0=15√2m as shown in the figure. The particle slides on the inner surface and reaches point B, a vertical distance h=15m below A and a distance r from the vertical centerline, where its velocity v makes an angle θ with the horizontal tangent to the bowl through B. If θ=15K∘. Find the value of K. (take g=10m/s2)
View Solution(a) Photoelectric threshold of metallic silver is λ=3800Å. Ultravilolet light of λ=260 nm is incident on silver surface. Calculate :
(i) the value of work function in joule and eV
Kmax of the emitted photoelectrons
(iii) vmax of the photoelectrons
(b) Ultraviolet light of wavelength 280 nm is used in an experiment on photoelectric effict with lithium (ϕ=2.5eV) cathode. Find
(i) the maximum kinetic energy of the photoelectrons
(ii) the stopping potential
(c) Find the maximum magnitude of the linear momentum of a photelectron emitted when light of wavelength 400 nm falls on a metal (ϕ=2.5eV).
(d) A monochromitc light source of intensity 5 mW emits 8×105 photons per second. This light ejects photoelectrons from a metal surface. The stopping potential for this set up is 2.0V . Calculate the work function of the metal.
(e) The maximum kinetic energy of photoelectrons emitted from a certain metallic surface is 30 eV when imonochromatic radiation of wavelength λ falls on it. When the same surface is illuminated with light of wavelength 2λ the maximum kinetic energy of photo electrons is observed to be 10 eV. Calculate the wavelength λ and determine the maximum wavelength of incident radiation for which photoelectrons can be emitted by this surface.
View Solution
