Draw an equilateral triangle. Find its circumcentre (C), incentre (I), centroid (G) and orthocentre (O). Write your observation.Solution in Marathi
The circumcentrem© , incentre (I) centroid (G) and orthocentre (O), coincide I, e. they are one and the same points
Topper's Solved these Questions
Similar Questions
If base of a parallelogram is 18 cm and its height is 11 cm, find its area.
View SolutionStatement I : If centroid and circumcentre of a triangle are known its orthocentre can be found
Statement II : Centroid, orthocentre and circumcentre of a triangle are collinear.07:18View SolutionABC is a triangle whose circumcentre, incentre and orthocentre are O, I and H respectively which lie inside the triangle, then :
03:14View SolutionIf S is the circumcentre, G the centroid, O the orthocentre of Δ ABC, then →SA+→SB+→SC=
05:22View SolutionIn an equilateral triangle, the incentre, circumcentre, orthocentre and centroid are :
02:18View SolutionIn a triangle, if orthocentre, circumcentre, incentre and centroid coincide, then the triangle must be
03:59View SolutionIf the orthocentre and the circucentre of are (-3,5,2) ,(6,2,5) then its centroid is
05:33View SolutionIn an equilateral triangle, the inradius, circumradius, and one of the exradii are in the ratio
02:27View SolutionIn ΔXYZ, I is incentre , O is orthocentre & C is circumcentre . ∠XOZ=2.5∠XCZ. Find ∠XIZ.
01:29View SolutionStatement I : If centroid and circumcentre of a triangle are known its orthocentre can be found
Statement II : Centroid, orthocentre and circumcentre of a triangle are collinear.07:18View SolutionThe vertices of a triangle are A(−10,8),B(14,8) and C(−10,26). Let G, I, H, O be the centroid, incentre, orthocentre, circumcentre respectively of ΔABC.
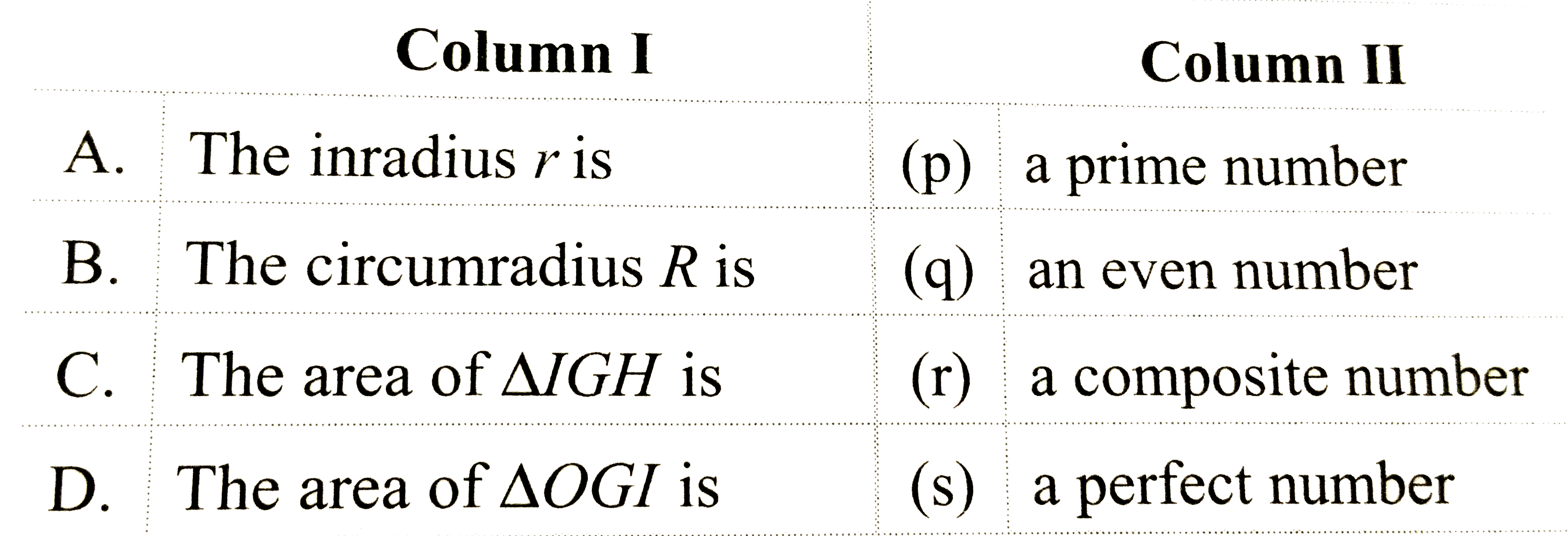14:00View SolutionDraw an isosceles triangle. Locate its centroid, orthocentre, circumcentre and in- centre. Write your observation.
03:14View SolutionIn a triangle, if orthocentre, circumcentre, incentre and centroid coincide, then the triangle must be_____
02:45View SolutionStatement I : If centroid and circumcentre of a triangle are known its orthocentre can be found
Statement II : Centroid, orthocentre and circumcentre of a triangle are collinear.04:21View SolutionThe incentre of a triangle coincides with the circumcentre, orthocentre and centroid in case of :
02:16View Solution