Fill in the gap :
The ratio of the areas of two similar triangles is equal to the square of the ratio of their _______.Solution in Assamese
Step by step video & image solution for Fill in the gap : The ratio of the areas of two similar triangles is equal to the square of the ratio of their _______. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The length of a diagonal of a square is 16cm. Find the length of the side of it.
View Solutiona number is selected from 1,2,3,....,15. what is the probability that the number is a multiple of 4
View SolutionWhich of the following is quadratic equation:
x2+√2x+3=0.
View SolutionProve that the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.
View SolutionThe ratio of area of Two similar triangles is equal to the ratio of the squares of any two corresponding sides.
View SolutionThe ratio of the the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides/altitudes.
View SolutionTheorem 6.6 : The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
View SolutionThe ratio of areas of two similar triangles is equal to the ratio of the squares of corresponding…….
View SolutionProve that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
View SolutionProve that " the ratio of areas of two similar triangles is equal to the square of the ratio of their altitudes.
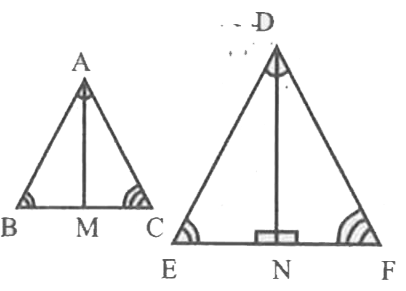
View SolutionProve that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
View SolutionProve that the ratio at the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
View SolutionProve that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
View SolutionTheorem 6.6 : The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
View SolutionProve that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
View SolutionProve that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
View Solution
