The area of an equilateral triangle ABC is 17320.5cm2.With each vertex of the triangle as center,a circle is drawn with radius equal to half the length of the side of the triangle(seeFig.12.28).Find the area of the shaded region.(use π=3.14 and √3=1.73205)
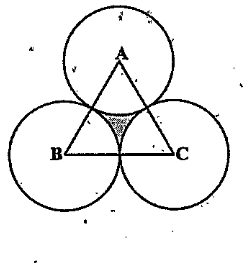 Solution in Assamese
Solution in Assamese
Step by step video & image solution for The area of an equilateral triangle ABC is 17320.5cm^2.With each vertex of the triangle as center,a circle is drawn with radius equal to half the length of the side of the triangle(seeFig.12.28).Find the area of the shaded region.(use pi=3.14 and sqrt3=1.73205) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREAS RELATED TO CIRCLESBOOK - KALYANI PUBLICATIONCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - EXERCISE
60 Videos
- AREAS OF SIMILAR TRIANGLESBOOK - KALYANI PUBLICATIONCHAPTER - AREAS OF SIMILAR TRIANGLESEXERCISE - EXAMPLE
1 Videos
- ARITHMATIC PROGRESSIONBOOK - KALYANI PUBLICATIONCHAPTER - ARITHMATIC PROGRESSIONEXERCISE - EXERCISE
68 Videos
Similar Questions
The inner circumference of a circular track is 220 m. The track is 7 m everywhere. Calculate the cost of putting a fence along the outer boundary at rupees 20per metre.
View SolutionABC is a triangle. D and E are two points on AB and AC such that DE and BC are parallel. If the area of DECB is m times the area of ADE then find DBAB .
View Solutionfor the A.P. 5,9,13,17,.... which term of the progression is 81.
View SolutionThe area of an equilateral triangle ABC is 17320.5 cm2. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (see Fig. 12.28). Find the area of the shaded region. (U
View SolutionThe area of an equilateral ΔABC is 17320.5 cm2. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (see the figure). Find the area of the shaded region. [Take π = 3.14 and √3 = 1.73205]
View SolutionFind the area of the shaded region, given that the radius of each circle is equal to 5 cm.
View SolutionMatch the following Column A to Column B

View SolutionFind out area of triangle OAB and BCD shown in figure :- ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R05_E01_014_Q01.png" width="80%"gt
View Solutionएक समबाहु त्रिभुज ABC का क्षेत्रफल 17320.5 cm2 है। इस त्रिभुज के प्रत्येक शीर्ष को केन्द्र मानकर त्रिभुज की भुजा के आधे के बराबर की त्रिज्या लेकर एक वृत्त खींचा जाता है। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।
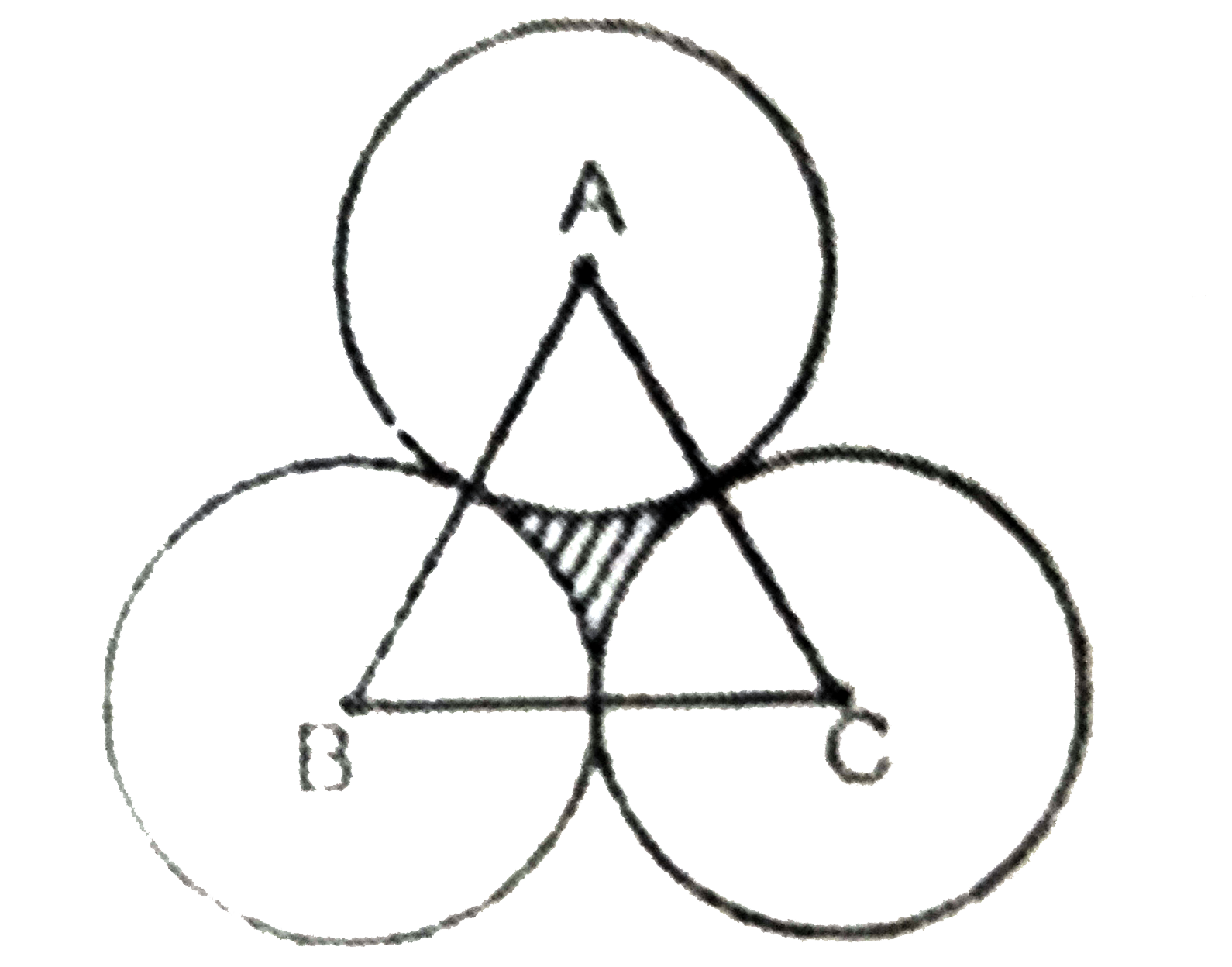
View Solutionचित्र में, 6 सेमी. भुजा वाला एक समबाहु त्रिभुज ABC एक वृत्त के अन्दर बनाया गया है | छायांकित भाग का क्षेत्रफल ज्ञात कीजिए | (π=3.14)
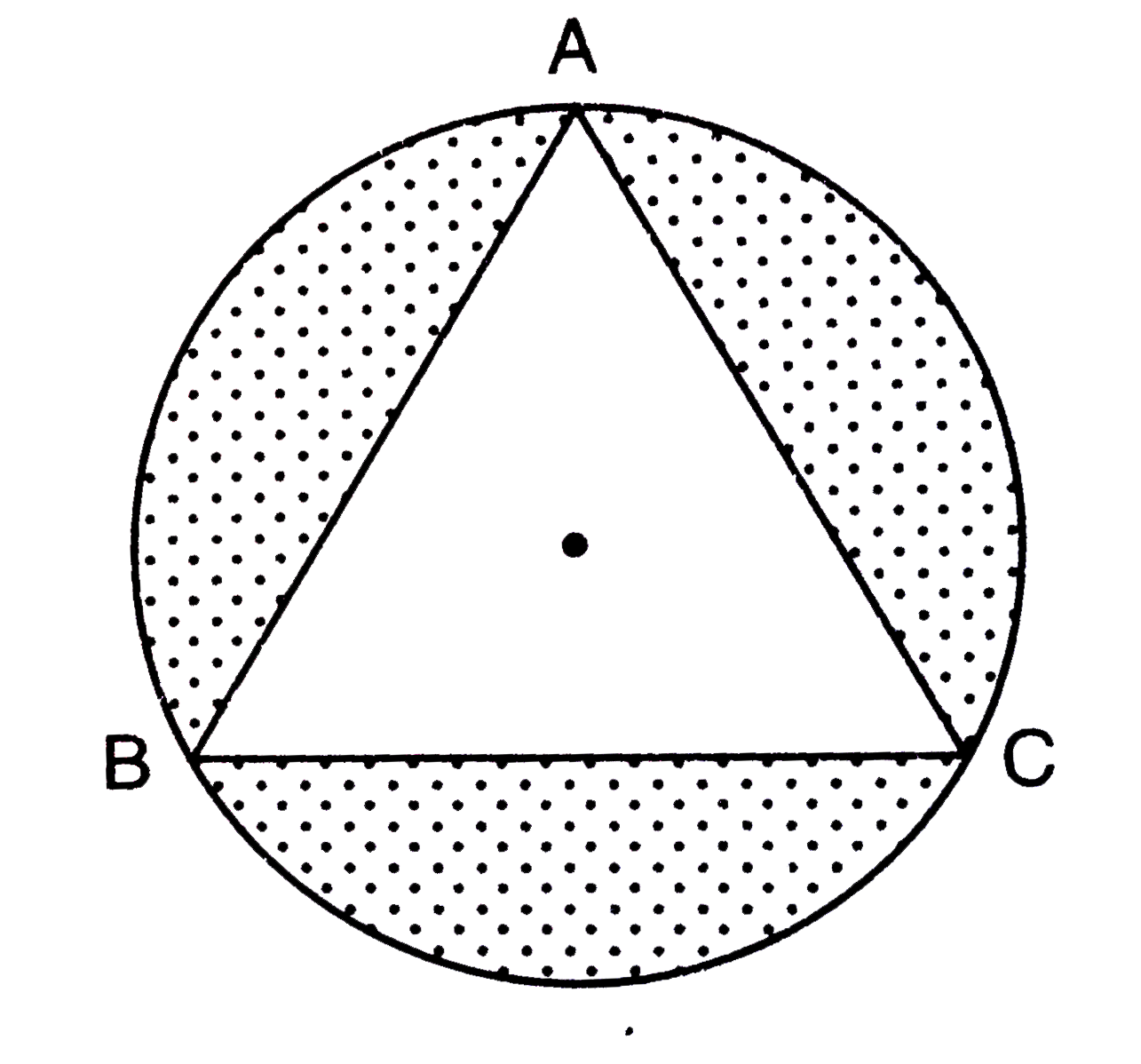
View Solutionएक समबाहु त्रिभुज ABC का क्षेत्रफल 17320.5 सेमी2 है । इस त्रिभुज के प्रत्येक शीर्ष को केंद्र मानकर त्रिभुज की भुजा के आधे के बराबर की त्रिज्या लेकर एक वृत्त खींचा जाता है ( देखिए आकृति )।छायांकित भाग का क्षेत्रफल ज्ञात कीजिए । ( π=3.14 और √3=1.73205 लीजिए )

View Solutionएक समबाहु त्रिभुज का क्षेत्रफल 17300cm2 है। त्रिभुज के प्रत्येक शीर्ष को केन्द्र लेकर एक वृत्त खींचा गया ह। वृत्त की त्रिज्या समबाहु त्रिभुज की भुजा की लंबाई के आधा है । त्रिभुज के उस भाग का क्षेत्रफल ज्ञात कीजिए जो वृत्त में नहीं है। (π=3.14 और √3=1.73)
View Solutionचित्र में ABC एक समबाहु त्रिभुज है जिसकी एक भुजा 20 सेमी है। त्रिभुज के प्रत्येक शीर्ष से 10 सेमी त्रिज्या के वृत्त खींचे गये हैं। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए। (π=3.14 लीजिए)
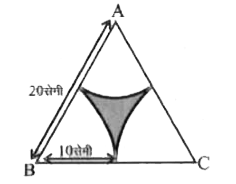
View SolutionThe area of an equilateral triangle ABC is 17320.5 cm2. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (see Fig. 12.28). Find the area of the shaded region. (Use π=3.14and√3= 1.73205)
View SolutionThe area of an equilateral triangle ABC is 17320.5cm2. With each vertex of the trianlge as centre, a circle is drawn with radius equal to half the length of the side of the triangle. Find the area of the shaded region .
View SolutionArea of an equilateral triangle is 17300 cm2. By taking each vertex of the triangle as centre, a circle is drawn at each vertex. The radius of thecircleis half of the length of the side of an equilateral triangle. Find the area of that portion of the triangle which is not included in the circle. (π=3.14 and √3=1.73)
View Solution
