A parallelogram ABCD has P the mid-point of DC and Q a point of AC such that CQ=14AC.PQ produced meets BC at R. Prove that:
PR=12DB.
To prove that PR = (1/2) DB in the given parallelogram ABCD with the specified points, we can follow these steps:
Step 1: Understand the Given Information
We have a parallelogram ABCD where:
- P is the midpoint of side DC.
- Q is a point on diagonal AC such that CQ = (1/4) AC.
- The line PQ produced meets BC at point R.
Step 2: Set Up the Coordinate System
Let’s assign coordinates to the points:
- A(0, 0)
- B(a, 0)
- C(a, b)
- D(0, b)
Since P is the midpoint of DC, we can find its coordinates:
- P = ((0 + a)/2, (b + b)/2) = (a/2, b)
For point Q, since CQ = (1/4) AC, we can find its coordinates:
- The coordinates of C are (a, b) and A are (0, 0).
- The vector AC = (a - 0, b - 0) = (a, b).
- Therefore, CQ = (1/4)(a, b) = (a/4, b/4).
- Thus, the coordinates of Q = C + CQ = (a, b) + (a/4, b/4) = (5a/4, 5b/4).
Step 3: Find the Equation of Line PQ
Using the coordinates of P and Q, we can find the slope of line PQ:
- Slope of PQ = (y2 - y1) / (x2 - x1) = (5b/4 - b) / (5a/4 - a) = (5b/4 - 4b/4) / (5a/4 - 4a/4) = (b/4) / (a/4) = b/a.
Now, we can write the equation of line PQ using point-slope form:
- y - y1 = m(x - x1)
- y - b = (b/a)(x - a/2)
- Rearranging gives us: y = (b/a)x + (b - (b/2)) = (b/a)x + b/2.
Step 4: Find the Equation of Line BC
The line BC can be represented as:
- The slope of BC = (b - 0) / (a - a) = undefined (vertical line).
- The equation of line BC is x = a.
Step 5: Find the Intersection Point R
To find the intersection point R, we substitute x = a into the equation of line PQ:
- y = (b/a)(a) + b/2 = b + b/2 = (3b/2).
- Therefore, R = (a, 3b/2).
Step 6: Find the Lengths PR and DB
Now, we need to find the lengths PR and DB:
- Length PR = Distance from P(a/2, b) to R(a, 3b/2):
PR = √((a - a/2)² + (3b/2 - b)²) = √((a/2)² + (b/2)²) = √((a²/4) + (b²/4)) = (1/2)√(a² + b²).
- Length DB = Distance from D(0, b) to B(a, 0):
DB = √((a - 0)² + (0 - b)²) = √(a² + b²).
Step 7: Prove PR = (1/2) DB
Now we can compare the lengths:
- PR = (1/2)√(a² + b²)
- DB = √(a² + b²)
Thus, we have:
PR = (1/2) DB.
Conclusion
We have proved that PR = (1/2) DB.
---
We have a parallelogram ABCD where:
- P is the midpoint of side DC.
- Q is a point on diagonal AC such that CQ = (1/4) AC.
- The line PQ produced meets BC at point R.
Let’s assign coordinates to the points:
- A(0, 0)
- B(a, 0)
- C(a, b)
- D(0, b)
- P = ((0 + a)/2, (b + b)/2) = (a/2, b)
- The coordinates of C are (a, b) and A are (0, 0).
- The vector AC = (a - 0, b - 0) = (a, b).
- Therefore, CQ = (1/4)(a, b) = (a/4, b/4).
- Thus, the coordinates of Q = C + CQ = (a, b) + (a/4, b/4) = (5a/4, 5b/4).
Using the coordinates of P and Q, we can find the slope of line PQ:
- Slope of PQ = (y2 - y1) / (x2 - x1) = (5b/4 - b) / (5a/4 - a) = (5b/4 - 4b/4) / (5a/4 - 4a/4) = (b/4) / (a/4) = b/a.
- y - y1 = m(x - x1)
- y - b = (b/a)(x - a/2)
- Rearranging gives us: y = (b/a)x + (b - (b/2)) = (b/a)x + b/2.
The line BC can be represented as:
- The slope of BC = (b - 0) / (a - a) = undefined (vertical line).
- The equation of line BC is x = a.
To find the intersection point R, we substitute x = a into the equation of line PQ:
- y = (b/a)(a) + b/2 = b + b/2 = (3b/2).
- Therefore, R = (a, 3b/2).
Now, we need to find the lengths PR and DB:
- Length PR = Distance from P(a/2, b) to R(a, 3b/2):
PR = √((a - a/2)² + (3b/2 - b)²) = √((a/2)² + (b/2)²) = √((a²/4) + (b²/4)) = (1/2)√(a² + b²).
DB = √((a - 0)² + (0 - b)²) = √(a² + b²).
Now we can compare the lengths:
- PR = (1/2)√(a² + b²)
- DB = √(a² + b²)
PR = (1/2) DB.
We have proved that PR = (1/2) DB.
Topper's Solved these Questions
- MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM)Book:ICSEChapter:MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM)Exercise:EXERCISE 12(B)
Explore 23 Videos
- MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM)Book:ICSEChapter:MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM)Exercise:EXERCISE 12(B)
Explore 23 Videos
- MENSURATION (PLANE FIGURE) Book:ICSEChapter:MENSURATION (PLANE FIGURE) Exercise:TOPIC-3 (4 Marks Questions)
Explore 8 Videos
- MID-POINT THEOREMBook:ICSEChapter:MID-POINT THEOREMExercise:4 MARKS QUESTION
Explore 15 Videos
Similar Questions
A parallelogram ABCD has P the mid-point of DC and Q a midpoint of AC such that CQ=14AC.PQ produced meets BC at R. Prove that:
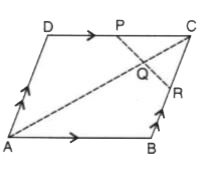
R is the mid-point of BC
View SolutionIn Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R. Prove that R is a mid-point of BC.
View SolutionIn Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R, prove that R is a mid-point of BC.
View SolutionIn figure, P is the mid-point of BC,,Q is the mid-point of AP , such that BQ produced meets AC at R. Prove that 3RA=CA
View SolutionIn parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that :
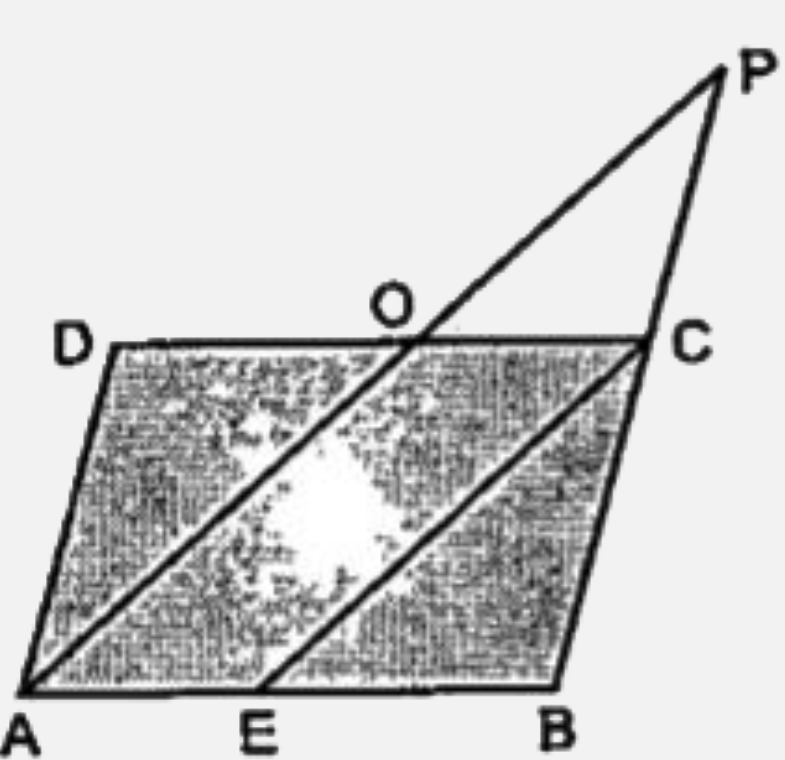
BP=2AD
View SolutionIn parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that:
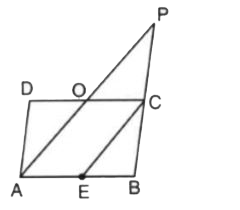
PB=2AD
View SolutionIn parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.
View SolutionIn parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that:

O is mid-point of AP.
View SolutionIn trapezium ABCD, AB is parallel to DC. P and Q are the mid-points of AD and BC respectively. BP produced meets CD produced at point E. Prove that :
PQ is parallel to AB.
View SolutionIn a parallelogram ABCD, P is a point on side AD such that 3AP = AD and Q is a point on BC such that 3CQ = BC. Prove that : AQCP is a parallelogram.
View Solution