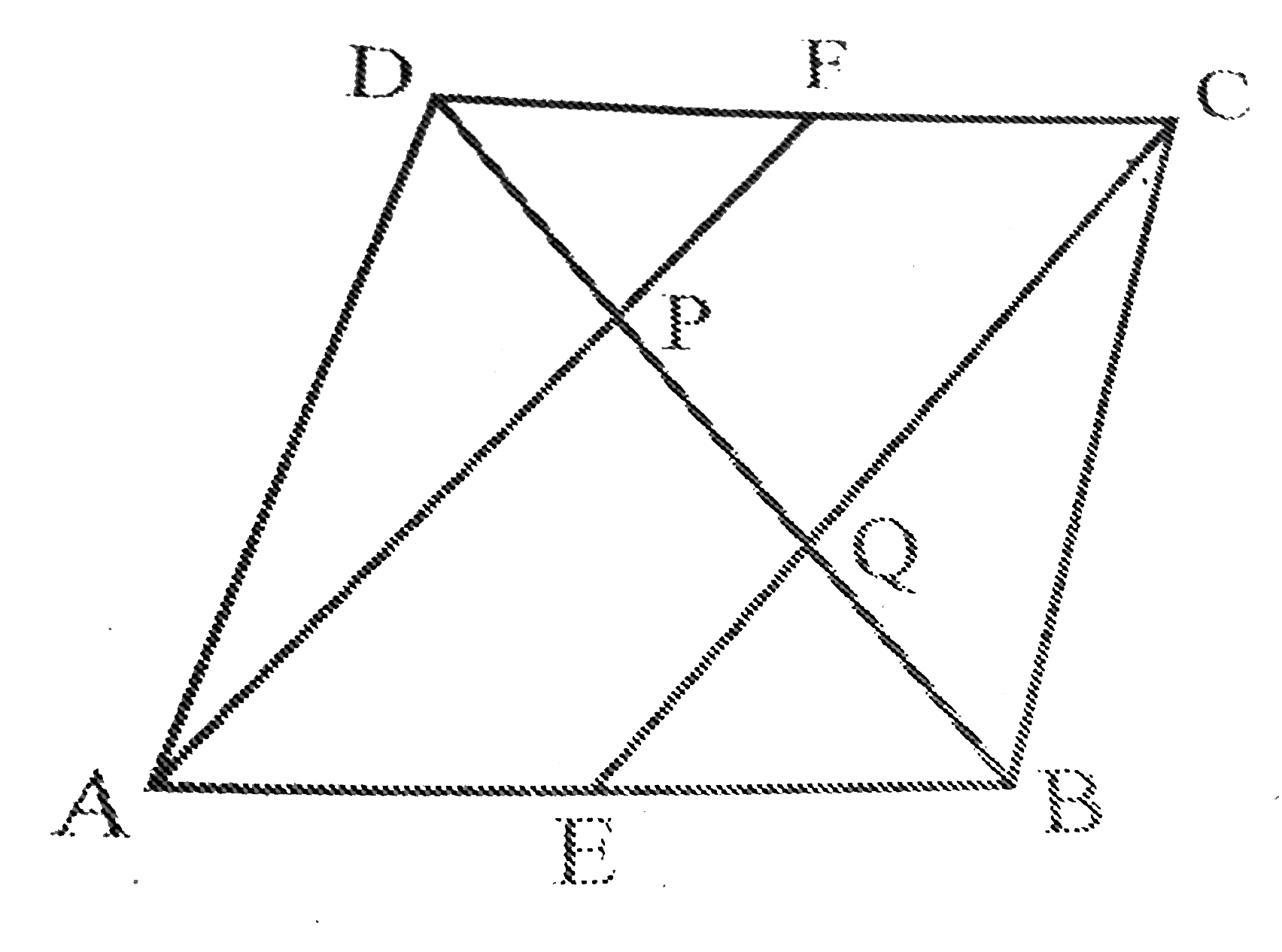
In parallelogram ABCD, E and F are mid-points of the sides AB and CD respectively. The lines segments AF and BF meet the line segments ED and EC at points G and H respectively. Prove that :
triangle HEB and FHC are congruent.
Step by step video & image solution for In parallelogram ABCD, E and F are mid-points of the sides AB and CD respectively. The lines segments AF and BF meet the line segments ED and EC at points G and H respectively. Prove that : triangle HEB and FHC are congruent. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM)BOOK - ICSECHAPTER - MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM)EXERCISE - EXERCISE 12(A)
23 Videos
- MENSURATION (PLANE FIGURE) BOOK - ICSECHAPTER - MENSURATION (PLANE FIGURE) EXERCISE - TOPIC-3 (4 Marks Questions)
8 Videos
- MID-POINT THEOREMBOOK - ICSECHAPTER - MID-POINT THEOREMEXERCISE - 4 MARKS QUESTION
15 Videos
Similar Questions
In parallelogram ABCD, E and F are mid-points of the sides AB and CD respectively. The lines segments AF and BF meet the line segments ED and EC at points G and H respectively. Prove that :
GEHF is a parallelogram.
View SolutionIn a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively. Show that the line segments AF and EC trisect the diagonal BD.
View SolutionIn a parallelogram ABCD, E and F are the mid-points of sides BC and AD respectively. Show that the line segment BF and ED trisect the diagonal AC.
View SolutionIn ΔABC,D,E and F are mid-point of sides AB ,BC and AC respectively , Prove that AE and DF bisect each other.
View SolutionD, E and F are the mid-points of the sides AB, BC and CA respectively of A ABC. AE meets DF at O. P and Q are the mid-points of OB and OC respectively. Prove that DPOF is a parallelogram.
View SolutionL and M are the mid-points of sides AB and DC respectively of parallelogram ABCD. Prove that segments DL and BM trisect diagonal AC.
View SolutionIn Figure, ABCD is a parallelogram. E and F are the mid-points of the sides AB and CD respectively. Prove that the line segments AF and CE triset (divide into three equal parts) the diagonal BD.
View SolutionABCD is a parallelogram, E and F are the mid-points of AB and CD respectively. GH is any line intersecting AD, EF and BC at G, P and H respectively. Prove that GP=PH
View SolutionD, E and F are the mid-points of the sides BC, CA and AB respectively of triangle ABC. Prove that:
BDEF is a parallelogram.
View SolutionIn a trapezium ABCD, if E and F be the mid-points of diagonal AC and BD respectively. Prove that EF=12(AB−CD).

View Solution
