A ball of mass 175g moves with an uniform velocity. The ball can be located with an error equal to 5500Å. If an effort is made to determine the velocity of the ball, what will be the uncertainity in this measurement?
To solve the problem using Heisenberg's uncertainty principle, we will follow these steps:
Step 1: Understand Heisenberg's Uncertainty Principle
Heisenberg's uncertainty principle states that the product of the uncertainties in position (Δx) and momentum (Δp) is greater than or equal to a constant, given by:
Δx⋅Δp≥h4π
where h is Planck's constant.
Step 2: Relate Momentum to Mass and Velocity
Momentum (p) is defined as the product of mass (m) and velocity (v):
p=m⋅v
Thus, the uncertainty in momentum (Δp) can be expressed as:
Δp=m⋅Δv
where Δv is the uncertainty in velocity.
Step 3: Substitute into the Uncertainty Principle
Substituting Δp into the uncertainty principle gives:
Δx⋅(m⋅Δv)≥h4π
Step 4: Rearrange the Equation
Rearranging the equation to solve for Δv:
Δv≥h4πmΔx
Step 5: Insert Known Values
We have the following values:
- Mass of the ball, m=175g=0.175kg (note: we will use grams in CGS units)
- Position uncertainty, Δx=5500Å=5500×10−8cm=5.5×10−5cm
- Planck's constant, h=6.626×10−27erg⋅s (in CGS units)
Now substituting these values into the equation:
Δv≥6.626×10−274⋅3.14⋅175⋅5.5×10−5
Step 6: Calculate the Uncertainty in Velocity
Calculating the denominator:
4⋅3.14⋅175⋅5.5×10−5≈0.000386g⋅cm/s
Now substituting back:
Δv≥6.626×10−270.000386≈1.718×10−23cm/s
Step 7: Final Result
Thus, the uncertainty in the velocity measurement (Δv) is approximately:
Δv≥1.718×10−23cm/s
Heisenberg's uncertainty principle states that the product of the uncertainties in position (Δx) and momentum (Δp) is greater than or equal to a constant, given by:
Δx⋅Δp≥h4π
where h is Planck's constant.
Momentum (p) is defined as the product of mass (m) and velocity (v):
p=m⋅v
Thus, the uncertainty in momentum (Δp) can be expressed as:
Δp=m⋅Δv
where Δv is the uncertainty in velocity.
Substituting Δp into the uncertainty principle gives:
Δx⋅(m⋅Δv)≥h4π
Rearranging the equation to solve for Δv:
Δv≥h4πmΔx
We have the following values:
- Mass of the ball, m=175g=0.175kg (note: we will use grams in CGS units)
- Position uncertainty, Δx=5500Å=5500×10−8cm=5.5×10−5cm
- Planck's constant, h=6.626×10−27erg⋅s (in CGS units)
Δv≥6.626×10−274⋅3.14⋅175⋅5.5×10−5
Calculating the denominator:
4⋅3.14⋅175⋅5.5×10−5≈0.000386g⋅cm/s
Δv≥6.626×10−270.000386≈1.718×10−23cm/s
Thus, the uncertainty in the velocity measurement (Δv) is approximately:
Δv≥1.718×10−23cm/s
Topper's Solved these Questions
- BOOK - ICSECHAPTER - STRUCTURE OF ATOMEXERCISE - Review Exercises35videos
STRUCTURE OF ATOM
- BOOK - ICSECHAPTER - STRUCTURE OF ATOMEXERCISE - Very Short Answer Type Questions30videos
STRUCTURE OF ATOM
- BOOK - ICSECHAPTER - STATES OF MATTER : GASES AND LIQUIDSEXERCISE - NCERT TEXT-BOOK EXERCISES (With Hints and Solutions)23videos
STATES OF MATTER : GASES AND LIQUIDS
- BOOK - ICSECHAPTER - THE s - BLOCK ELEMENTSEXERCISE - NCERT TEXT-BOOK. EXERCISES (WITH HINTS AND SOLUTIONS)55videos
THE s - BLOCK ELEMENTS
Similar Questions
A base ball of mass 200g is moving with velocity of 3×103cms−1 .If we can locte the base ball with an error equal to the magnitude of the wavelength of the light used (5000Å) how wil the uncertainty in momentum be used with the total momentum of the base ball?
View SolutionA base ball of mass 200g is moving with velocity of 3×103cms−1. If we can locate the base ball with an error equal to the magnitude of the wavelength of the light used (5000Å). How will the uncertainty in momentum be used with the total momentum of the base ball?
View SolutionA heavy ball of mass 2M moving with a velocity v0 collides elastically head on with a cradle of three identical ball each of mass M as shown in figure. Determine the velocity of each ball after collision.
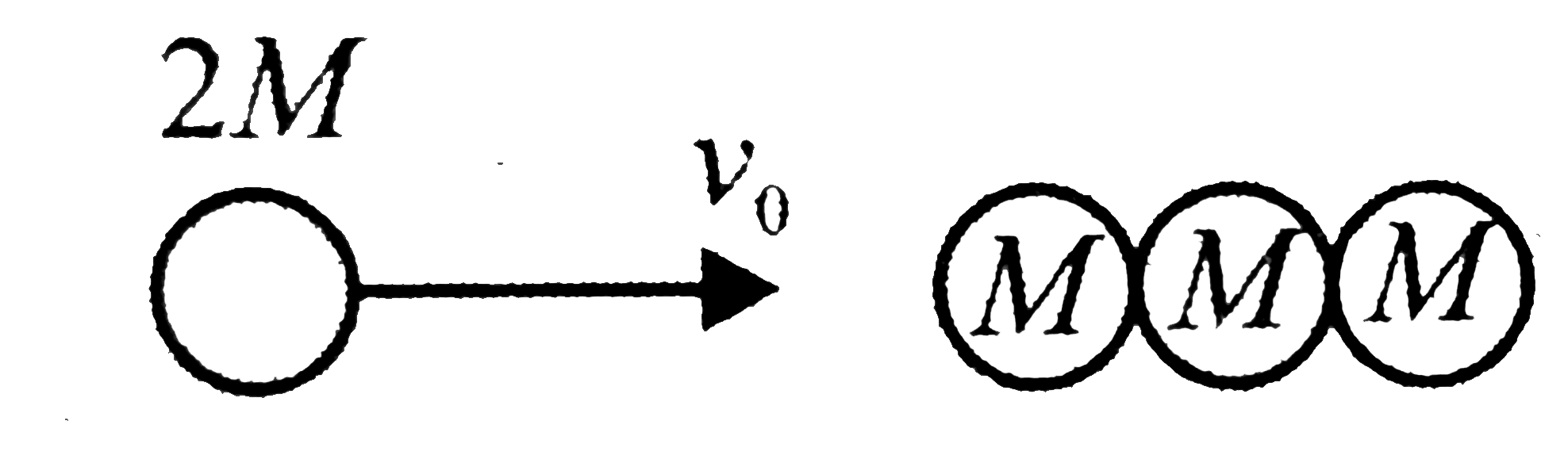 View Solution
View SolutionA ball of mass 0.2 kg moves with a velocity of 20m/sec and it stops in 0.1 sec , then the force on the ball is
View SolutionA ball of mass 0.2 kg moves with a velocity of 20m/sec and it stops in 0.1 sec , then the force on the ball is
View SolutionA ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision
View SolutionA ball of mass m1 is moving with velocity 3v. It collides head on elastically with a stationary ball of mass m2 . The velocity of both the balls become v after collision. Then the value of the ratio m2m1 is
View SolutionA boy is sitting in a car moving with uniform velocity. The boy throws a ball vertically upwards which falls back into his hands. A man standing on the road watches the motion of the ball. The path of the motion of the ball will be:
View SolutionA ball of mass 1 kg moving with velocity →v=3ˆi+4ˆj collides with a wall and after collision velocity of the ball is −2ˆi+6ˆj . Which of the following unit vectors is perpendicular to wall?
View SolutionA ball of mass 200g is moving with a velocity of 10msec−1 . If the error in measurement of velocity is 0.1%, the uncertainty in its position is :
View Solution

