A ball of mass 1 kg moving with velocity →v=3ˆi+4ˆj collides with a wall and after collision velocity of the ball is −2ˆi+6ˆj . Which of the following unit vectors is perpendicular to wall?
15(−3ˆi−4ˆj)
1√29(5ˆi+2ˆj)
1√40−(2ˆi+6ˆj)
1√40(5ˆi−2ˆj)
The correct Answer is:B
To find the unit vector that is perpendicular to the wall after the collision of the ball, we need to follow these steps:
Step 1: Determine the initial and final velocities of the ball.
- Initial velocity of the ball:
→vi=3^i+4^j
- Final velocity of the ball after collision:
→vf=−2^i+6^j
Step 2: Calculate the change in velocity.
The change in velocity (Δ→v) is given by:
Δ→v=→vf−→vi
Substituting the values:
Δ→v=(−2^i+6^j)−(3^i+4^j)
Δ→v=−2^i+6^j−3^i−4^j
Δ→v=(−2−3)^i+(6−4)^j
Δ→v=−5^i+2^j
Step 3: Find the magnitude of the change in velocity.
The magnitude of Δ→v is calculated as follows:
|Δ→v|=√(−5)2+(2)2
|Δ→v|=√25+4=√29
Step 4: Calculate the unit vector in the direction of the change in velocity.
The unit vector ^n in the direction of Δ→v is given by:
^n=Δ→v|Δ→v|
Substituting the values:
^n=−5^i+2^j√29
Step 5: Identify the unit vector perpendicular to the wall.
Since the impulse acts in the direction of the change in momentum, which is the same as the change in velocity, the unit vector we found is perpendicular to the wall. Thus, the unit vector perpendicular to the wall is:
^n=−5√29^i+2√29^j
Final Answer:
The unit vector perpendicular to the wall is:
^n=−5^i+2^j√29
---
- Initial velocity of the ball:
→vi=3^i+4^j
- Final velocity of the ball after collision:
→vf=−2^i+6^j
The change in velocity (Δ→v) is given by:
Δ→v=→vf−→vi
Substituting the values:
Δ→v=(−2^i+6^j)−(3^i+4^j)
Δ→v=−2^i+6^j−3^i−4^j
Δ→v=(−2−3)^i+(6−4)^j
Δ→v=−5^i+2^j
The magnitude of Δ→v is calculated as follows:
|Δ→v|=√(−5)2+(2)2
|Δ→v|=√25+4=√29
The unit vector ^n in the direction of Δ→v is given by:
^n=Δ→v|Δ→v|
Substituting the values:
^n=−5^i+2^j√29
Since the impulse acts in the direction of the change in momentum, which is the same as the change in velocity, the unit vector we found is perpendicular to the wall. Thus, the unit vector perpendicular to the wall is:
^n=−5√29^i+2√29^j
The unit vector perpendicular to the wall is:
^n=−5^i+2^j√29
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - LEVEL - 2 PARAGRAPH QUESTIONS2videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE MAIN (ARCHIVE)53videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - Level - 1 PARAGRAPH QUESTIONS3videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)89videos
ELECTROSTATICS
- BOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )111videos
GASEOUS STATE & THERMODYNAMICS
Similar Questions
A ball A moving with momentum 2ˆi+4ˆj collides with identical ball B moving with momentum 6ˆj . After collision momentum of ball B is 10ˆj . Which of the following statement is correct?
View SolutionA ball of mass m, travelling with velocity 2ˆi+3ˆj receives an impulse −3mˆi. What is the velocity of the ball immediately afterwards?
View Solution
Knowledge Check
- Question 1 - Select One
A ball weighing 4 kg and moving with velocity of 8 m/sec. Collides with a stationary ball of mass 12 kg. After the collision, the two balls move together. The final velocity is
A0B2 m/secC8 m/secD16 m/sec
A particle of mass m moving with a velocity (3ˆi+2ˆj)ms−1 collides with another body of mass M and finally moves with velocity (−2ˆi+ˆj)ms−1. Then during the collision
View Solutionp1ˆi+p2ˆj is a unit vector perpendicular to 4ˆi−3ˆj if
View Solutiona1ˆi+a2ˆj is a unit vector perpendicular to 4ˆi−3ˆj if
View SolutionA ball of mass m moving with velocity v0 collides with a wall as shown in Fig. After impact it rebounds with a velocity' (v0)/2The component of impulse acting on the ball along the wall is
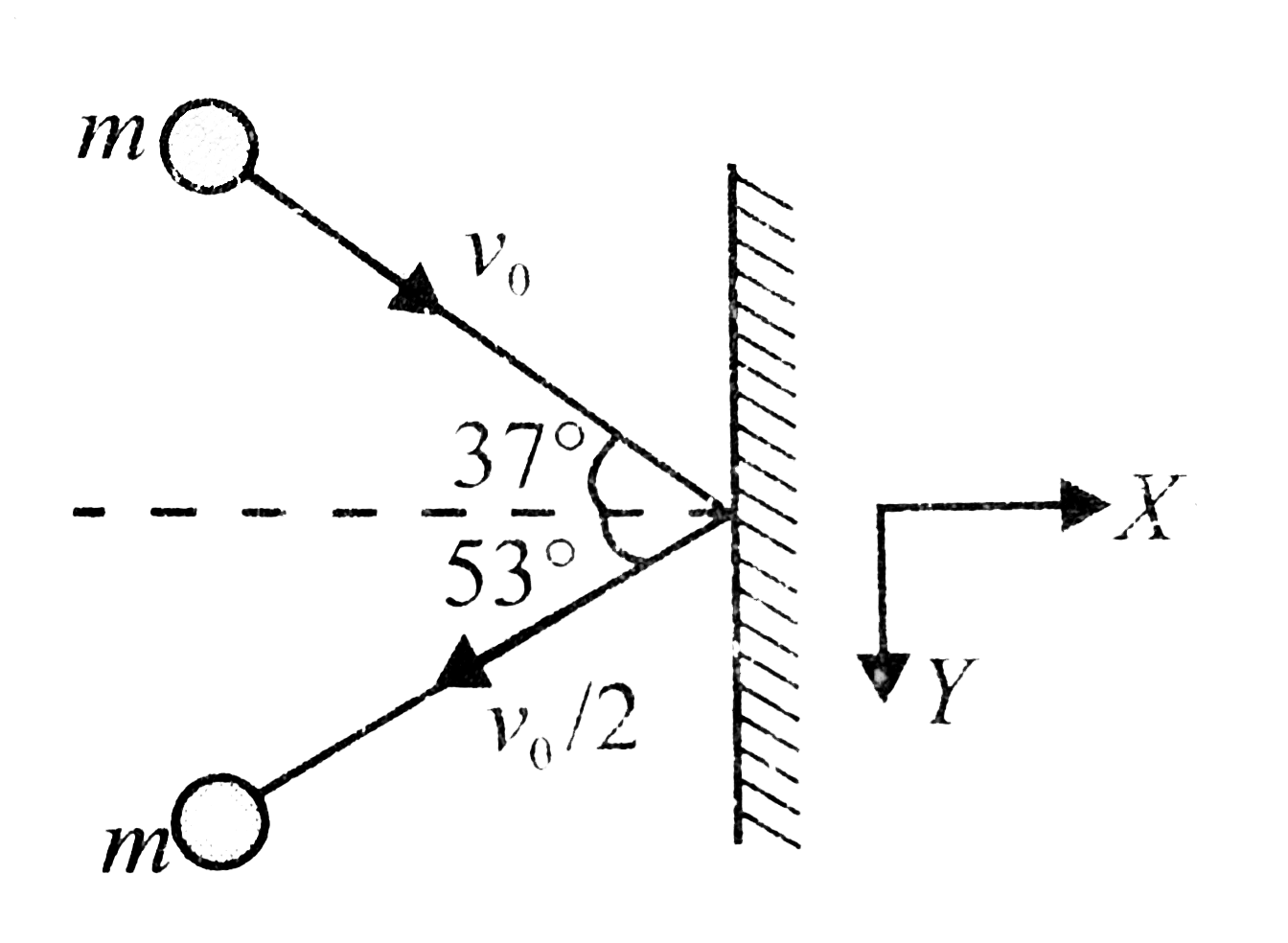 View Solution
View SolutionA small sphere of mass 1kg is moving with a velocity (6ˆi+ˆj)m/s . It hits a fixed smooth wall and rebounds with velocity (4ˆi+ˆj)m/s. The coefficient of restitution between the sphere and the wall is
View SolutionA small sphere of mass m=1kg is moving with a velocity (4ˆi−ˆj)m/s. it hits a fixed smooth wall and rebounds with velocity (ˆi+3ˆj)m/s. The coefficient of restitution between the sphere and the wall is n/16. Find the value of n.
View SolutionA ball of mass 1 kg moving with a velocity of 0.4 ms−1 collides with another stationary ball. After the collision, the first ball moves with a velocity of 0.3ms1 in a direction making an angle of 90∘ with its initial direction. The momentum of the second ball after the collision will be (in kg ms−1)
View Solution

