The position and velocity of earth can be determined simultaneously with a fair degree of accuracy.Comment.
The correct Answer is:1
To address the question regarding the simultaneous determination of the position and velocity of Earth, we can follow these steps:
Step 1: Understand the Statement
The statement claims that the position and velocity of Earth can be determined simultaneously with a fair degree of accuracy.
Hint: Consider what is meant by "simultaneously" and "accuracy" in the context of measurement.
Step 2: Define Position and Velocity
Position refers to the location of an object in space, while velocity refers to the speed of the object in a given direction. For Earth, we can determine its position in its orbit around the Sun and its rotational position on its axis.
Hint: Think about how we measure position (e.g., using coordinates) and velocity (e.g., speed and direction).
Step 3: Introduce Heisenberg Uncertainty Principle
The Heisenberg Uncertainty Principle states that it is impossible to simultaneously know both the position (Δx) and momentum (Δp) of a particle with complete accuracy. The principle can be mathematically expressed as:
Δx⋅Δp≥h2π
where h is Planck's constant.
Hint: Reflect on how this principle applies to measurements in quantum mechanics and whether it can be extended to macroscopic objects like Earth.
Step 4: Analyze the Implications
According to the Heisenberg Uncertainty Principle, if we try to measure the position of Earth very accurately (small Δx), the uncertainty in its momentum (and thus velocity) will increase (large Δp), and vice versa. This means that we cannot determine both quantities with high precision at the same time.
Hint: Consider how this principle applies to objects of different scales—does it only apply to quantum particles or can it also apply to larger objects?
Step 5: Conclude
Thus, while we can measure the position and velocity of Earth, we cannot do so simultaneously with complete accuracy. There will always be some uncertainty in either the position or the velocity when one is measured more accurately.
Hint: Think about real-world applications—how do scientists and astronomers deal with these uncertainties when observing celestial bodies?
Final Statement
In conclusion, the statement that the position and velocity of Earth can be determined simultaneously with a fair degree of accuracy is not correct. Due to the Heisenberg Uncertainty Principle, there will always be a trade-off in the accuracy of these measurements.
The statement claims that the position and velocity of Earth can be determined simultaneously with a fair degree of accuracy.
Position refers to the location of an object in space, while velocity refers to the speed of the object in a given direction. For Earth, we can determine its position in its orbit around the Sun and its rotational position on its axis.
The Heisenberg Uncertainty Principle states that it is impossible to simultaneously know both the position (Δx) and momentum (Δp) of a particle with complete accuracy. The principle can be mathematically expressed as:
Δx⋅Δp≥h2π
where h is Planck's constant.
According to the Heisenberg Uncertainty Principle, if we try to measure the position of Earth very accurately (small Δx), the uncertainty in its momentum (and thus velocity) will increase (large Δp), and vice versa. This means that we cannot determine both quantities with high precision at the same time.
Thus, while we can measure the position and velocity of Earth, we cannot do so simultaneously with complete accuracy. There will always be some uncertainty in either the position or the velocity when one is measured more accurately.
In conclusion, the statement that the position and velocity of Earth can be determined simultaneously with a fair degree of accuracy is not correct. Due to the Heisenberg Uncertainty Principle, there will always be a trade-off in the accuracy of these measurements.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - STRUCTURE OF ATOMEXERCISE - Fill in the Blanks Type Questions20videos
STRUCTURE OF ATOM
- BOOK - ICSECHAPTER - STRUCTURE OF ATOMEXERCISE - Assertion-Reason Type Questions6videos
STRUCTURE OF ATOM
- BOOK - ICSECHAPTER - STRUCTURE OF ATOMEXERCISE - Objective (MCQ) TYPE Questions67videos
STRUCTURE OF ATOM
- BOOK - ICSECHAPTER - STATES OF MATTER : GASES AND LIQUIDSEXERCISE - NCERT TEXT-BOOK EXERCISES (With Hints and Solutions)23videos
STATES OF MATTER : GASES AND LIQUIDS
- BOOK - ICSECHAPTER - THE s - BLOCK ELEMENTSEXERCISE - NCERT TEXT-BOOK. EXERCISES (WITH HINTS AND SOLUTIONS)55videos
THE s - BLOCK ELEMENTS
Similar Questions
Knowledge Check
- Question 1 - Select One
The sign of a is positive. The sign of b is negative. If it can be determined, what is the sign of the mean of a and b?
APositiveBNegativeCBoth positive and negativeDCannot be determined from the given information.
Assertion (A) : The position of electron can be determined with the help of an electronic microscope.
Reason (R) : The product of uncertainty in momentum and the uncertainty in the position of an electron cannot be less than a finite limit.View SolutionIt is impossible to determine simultaneously the position of velocity of small microscopic particle such as electron , proton or neutron with accuracy .This is called Heisenberg's uncertainty principle. Mathematically, it is represented as Δx.Δp≥h4π,Δx is uncertainty in position Δp is uncertainty in momentum.
View SolutionIf position and momentum of an electron are determined at a time then value of ΔP is obtained 3ΔX, now the uncertainity
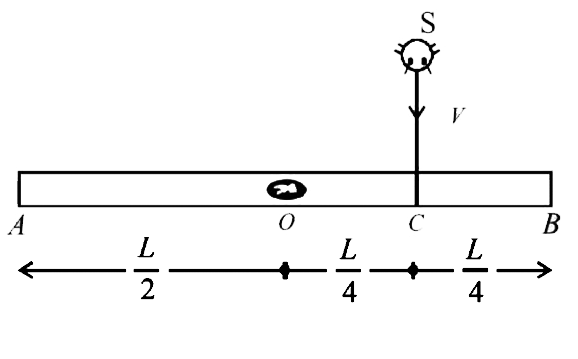
in velocity of electron will be :−View SolutionA homogeneous rod AB of length L = 1.8 m and mass M is pivoted at the center O in such a way that it can rotate it can rotate freely position. An insect S of the same mass M falls vertically with speed V on the point C, midway between the points O and B. Immediately after falling, the insect moves towards the end B such that the rod rotates with a constant angular velocity omega.
(a) Determine the angular velocity ω in terms of V and L.
(b) If the insect reaches the end B when the rod has turned through an angle of 90∘, determine V.
 View Solution
View SolutionWerner Heisenberg considered the limits of how precisely we can measure the properties of an electron or other microscopic particle. He determined that there is a fundamental limit to how closely we can measure both position and momentum. The more accurately we measure the momentum of a particle, the less accurately we can determine its position. The converse also true. This is summed up in what we now call the Heisenberg uncertainty principle.
The equation si δx.δ(mv)≥h4π
The uncertainty in the position or in the momentum of a marcroscopic object like a baseball is too small to observe. However, the mass of microscopic object such as an electon is small enough for the uncertainty to be relatively large and significant.
If the uncertainties in position and momentum are equal, the uncertainty in the velocity is :View SolutionWerner Heisenberg considered the limits of how precisely we can measure the properties of an electron or other microscopic particle. He determined that there is a fundamental limit to how closely we can measure both position and momentum. The more accurately we measure the momentum of a particle, the less accurately we can determine its position. The converse also true. This is summed up in what we now call the Heisenberg uncertainty principle.
The equation si δx.δ(mv)≥h4π
The uncertainty in the position or in the momentum of a marcroscopic object like a baseball is too small to observe. However, the mass of microscopic object such as an electon is small enough for the uncertainty to be relatively large and significant.
If the uncertainty in velocity and position is same, then the uncertainty in momentum will be :View SolutionA particle simple harmonic motion completes 1200 oscillations per minute and passes through the mean position with a velocity 3.14ms−1. Determine displacement of the particle from its mean position. Also obtain the displacement equation of the particle if its displacement be zero at the instant t=0.
View Solution

