AB is a diameter of a circle with centre C = (-2, 5). If A = (3, -7). Find
the length of radius AC
To find the length of the radius AC in the given circle, we will use the distance formula. Here are the steps to solve the problem:
1. Identify the Coordinates:
- The center of the circle C is given as (−2,5).
- The point A is given as (3,−7).
2. Use the Distance Formula:
The distance d between two points (x1,y1) and (x2,y2) is given by the formula:
d=√(x2−x1)2+(y2−y1)2
Here, we will let (x1,y1)=(3,−7) for point A and (x2,y2)=(−2,5) for center C.
3. Substitute the Coordinates into the Formula:
AC=√((−2)−3)2+(5−(−7))2
Simplifying this:
AC=√(−5)2+(5+7)2
4. Calculate the Squares:
AC=√25+(12)2
AC=√25+144
5. Add the Values:
AC=√169
6. Find the Square Root:
AC=13
Conclusion:
The length of the radius AC is 13 units.
---
- The center of the circle C is given as (−2,5).
- The point A is given as (3,−7).
The distance d between two points (x1,y1) and (x2,y2) is given by the formula:
d=√(x2−x1)2+(y2−y1)2
Here, we will let (x1,y1)=(3,−7) for point A and (x2,y2)=(−2,5) for center C.
AC=√((−2)−3)2+(5−(−7))2
Simplifying this:
AC=√(−5)2+(5+7)2
AC=√25+(12)2
AC=√25+144
AC=√169
AC=13
The length of the radius AC is 13 units.
Topper's Solved these Questions
Similar Questions
AB is a diameter of a circle with centre C = (-2, 5). If A = (3, -7). Find
the coordinates of B.
View SolutionIn the figure, AB is a diameter of the circle with centre O and OA = 7cm. Find the area of the shaded region
View SolutionThe co-ordinates of the end points of a diameter of a circle are (3, -2) and (-3, 6). Find the co-ordinates of the centre and radius.
View SolutionIn the given figure AB is the diameter of a circle with centre O . If chord AC = chord AD, prove that :
(i) are BC=areDB
(ii) AB is bisector of ∠CAD.
Further, if the length of are AC is twice the length of are BC , find :
(i) ∠BAC
(ii) ∠ABC
View SolutionIn the given figure, AB and PQ are perpendicular diameters of the circle whose centre is O and radius OA = 7 cm. Find the area of the shade region.

View SolutionAB is a diameter of a circle with centre O. Chord CD is equal to radius OC. AC and BD produced intersect at P. Prove that : ∠APB=60∘
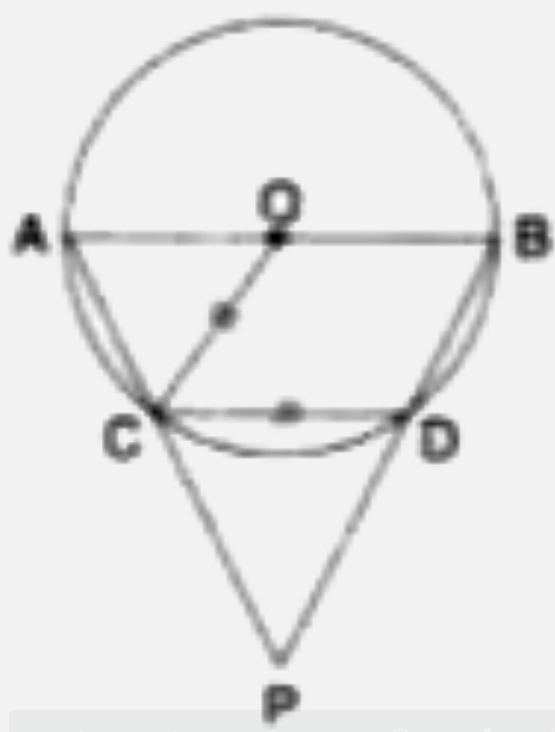
View SolutionOne end of a diameterof a circle is at (2,3) and the centre is (−2,5), find the coordinates of the other end of the diameter.
View SolutionThe end points of a diameter of a circle are (1,-1) and (3,5). Find the equation of the circle. Also find its centre and radius.
View SolutionAB is a diameter of the circle with centre O and chord CD is equal to radius OC (fig). AC and BD proudced meet at P. Prove that ∠CPD=60∘.
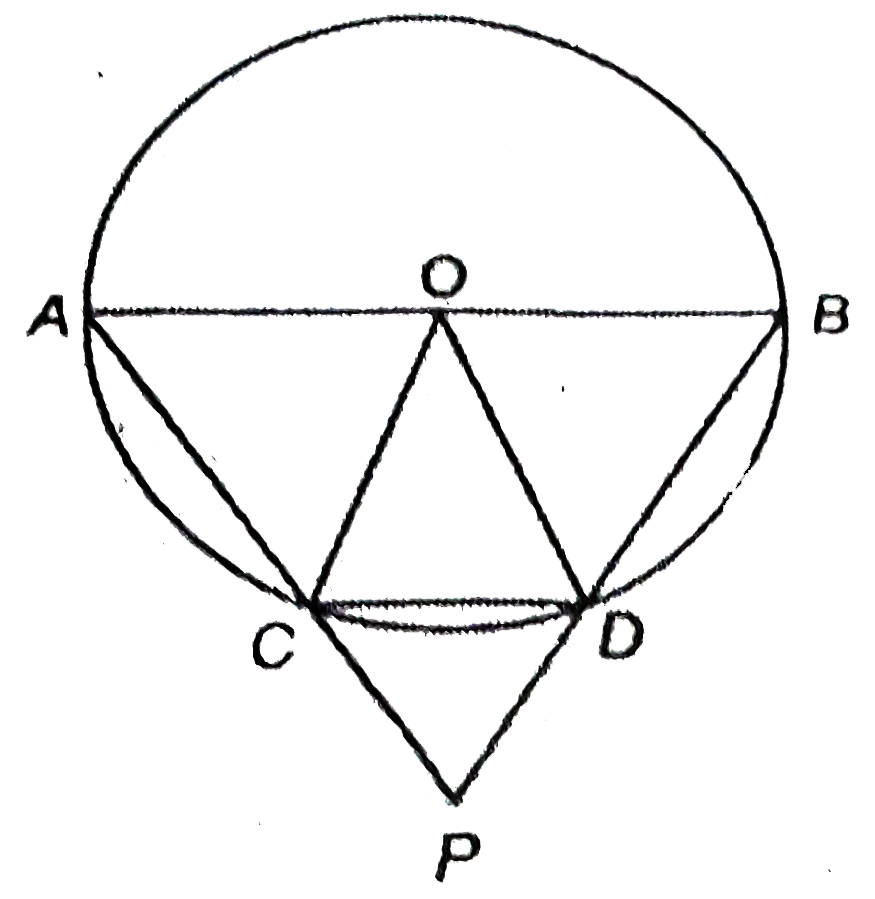
View SolutionABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AD and BC produced meet at P, show that APB=60∘ .
View Solution
