In the given figure ABC is a triangle and BC is parallel to the Y-axis. AB and AC intersects the y-axis at Pand Q respectively.

(i) Write the coordinates of A.
The correct Answer is:(4, 0)
Step by step video, text & image solution for In the given figure ABC is a triangle and BC is parallel to the Y-axis. AB and AC intersects the y-axis at Pand Q respectively. (i) Write the coordinates of A. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
Similar Questions
In the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.
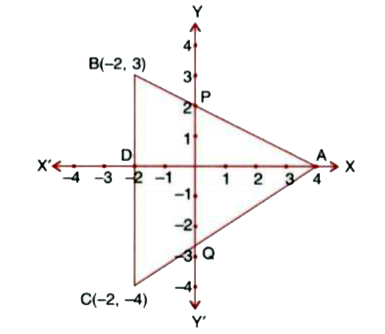
Write the co-ordinates of A.View SolutionIn the given figure ABC is a triangle and BC is parallel to the Y-axis. AB and AC intersects the y-axis at Pand Q respectively.

(iii) Find the ratio in which Q divides AC.View SolutionIn the given figure ABC is a triangle and BC is parallel to the Y-axis. AB and AC intersects the y-axis at Pand Q respectively.
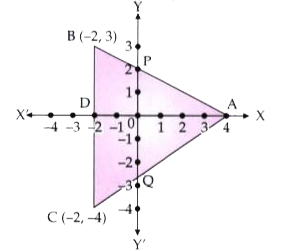
(iv) Find the equation of the line AC.View SolutionIn the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.

Find the equation of the line AC.View SolutionIn the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.
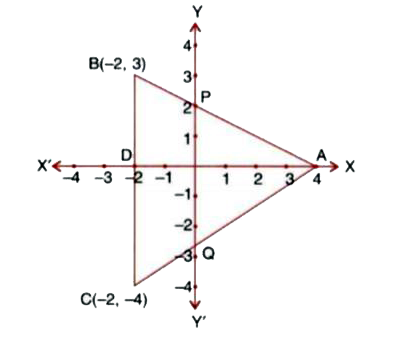
Find the length of AB and AC.View SolutionIn the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.
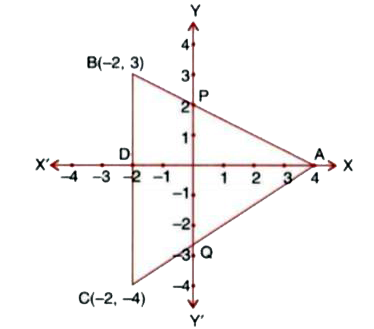
Find the ratio in which divides AC.View SolutionIn the given figure, ABC is a triangle. DE is parallel to BC and ADDB=32

Determine the ratios and ADABView SolutionThe side AB of an equilateral triangle ABC is parallel to the x-axis. Find the slopes of all its sides.
 View Solution
View SolutionIn the given figure, AP is parallel to BC, BP is parallel to CQ. Prove that the areas of triangles ABC and BQP are equal.
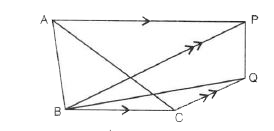 View Solution
View SolutionABC is a triangle A line is drawn parallel to BC to meet AB and AC in D and E respectively. Prove that the median through A bisects DE.
View Solution

