ABC is a triangle A line is drawn parallel to BC to meet AB and AC in D and E respectively. Prove that the median through A bisects DE.
To prove that the median through vertex A bisects the line segment DE, where D and E are points on sides AB and AC of triangle ABC respectively, and DE is parallel to BC, we can follow these steps:
Step 1: Define the Points
Let:
- A = (0, 0) (position vector of point A)
- B = (b1, b2) (position vector of point B)
- C = (c1, c2) (position vector of point C)
Step 2: Determine the Midpoint of BC
The midpoint M of segment BC can be calculated using the midpoint formula:
M=(b1+c12,b2+c22)
Step 3: Use Parallel Lines
Since DE is parallel to BC, the segments AD and AE are proportional to AB and AC respectively. Let:
- D divides AB in the ratio k:1
- E divides AC in the ratio m:1
Using the section formula, we can express the position vectors of points D and E as:
D=(kb1+0k+1,kb2+0k+1)=(kb1k+1,kb2k+1)
E=(mc1+0m+1,mc2+0m+1)=(mc1m+1,mc2m+1)
Step 4: Find the Midpoint of DE
Now, we find the midpoint P of segment DE:
P=⎛⎜⎝kb1k+1+mc1m+12,kb2k+1+mc2m+12⎞⎟⎠
Step 5: Find the Median from A to BC
The median from A to the midpoint M of BC is given by:
M=(b1+c12,b2+c22)
Step 6: Show that P = M
To prove that the median bisects DE, we need to show that P (the midpoint of DE) is equal to M (the midpoint of BC).
Since DE is parallel to BC, the ratios in which D and E divide AB and AC must be equal (i.e., k = m). Therefore, we can substitute k = m in our expressions for P and M, leading to:
P=M
Conclusion
Thus, we have shown that the median from A bisects the line segment DE, as required.
---
Let:
- A = (0, 0) (position vector of point A)
- B = (b1, b2) (position vector of point B)
- C = (c1, c2) (position vector of point C)
The midpoint M of segment BC can be calculated using the midpoint formula:
M=(b1+c12,b2+c22)
Since DE is parallel to BC, the segments AD and AE are proportional to AB and AC respectively. Let:
- D divides AB in the ratio k:1
- E divides AC in the ratio m:1
D=(kb1+0k+1,kb2+0k+1)=(kb1k+1,kb2k+1)
E=(mc1+0m+1,mc2+0m+1)=(mc1m+1,mc2m+1)
Now, we find the midpoint P of segment DE:
P=⎛⎜⎝kb1k+1+mc1m+12,kb2k+1+mc2m+12⎞⎟⎠
The median from A to the midpoint M of BC is given by:
M=(b1+c12,b2+c22)
To prove that the median bisects DE, we need to show that P (the midpoint of DE) is equal to M (the midpoint of BC).
P=M
Thus, we have shown that the median from A bisects the line segment DE, as required.
Similar Questions
In a triangle ABC , let P and Q be points on AB and AC respectively such that PQ∣∣BC . Prove that the median AD bisects PQ.
View SolutionM and N divide the side AB of a triangle ABC into three equal parts . Through M and N, lines are drawn parallel to BC and intersecting AC at points P and Q respectively. Prove that P and Q divide AC into three equal parts.
View SolutionIn the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.
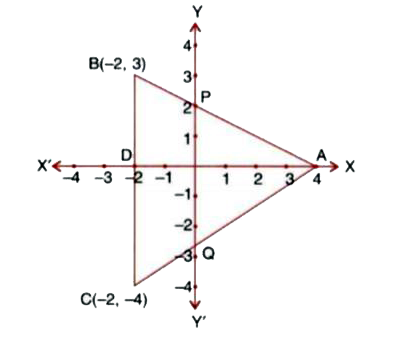
Find the length of AB and AC.
View SolutionThe incircle of an isoceles triangle ABC, with AB=AC, touches the sides AB,BC and CA at D,E and F respecrively. Prove that E bisects BC.
View SolutionIn the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.

Find the equation of the line AC.
View SolutionIn triangle ABC, D and E are points on side AB such that AD = DE = EB. Through D and E, lines are drawn parallel to BC which meet side AC at points F and G respectively. Through F and Glines are drawn parallel to AB which meet side BC at points M and N respectively.
Prove that : BM = MN = NC.
View SolutionAD is a median of ΔABC . The bisector of ∠ADB and ∠ADC meet AB and AC in E and F respectively. Prove that EF||BC
View SolutionIn the following figure, F and E are points on the side AD of the triangle ABD. Through F a line is drawn parallel to AB to meet BD at point C .
Prove that : ar (ΔACE)=ar (quad . BCEF )
View SolutionThe side AC of a triangle ABC is produced to point E so that CE=12 AC. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meet AC at point P and EF at point R respectively. Prove that:
3DF=EF
View SolutionThe bisectors of the angles B and C of a triangle ABC , meet the opposite sides in D and E respectively. If DE||BC , prove that the triangle is isosceles.
View Solution
