In ionic solids AB and CD , radius -ratios are x and y respectively. If x +y=0.75 and x-y=0.25 then cations in AB and CD are respectively in
T-voids, O-voids
O-voids , T-voids
T-voids, T-voids
O-voids , O-voids
The correct Answer is:B
To solve the problem, we need to find the values of x and y from the given equations and then determine the coordination geometry of the cations in the ionic solids AB and CD.
1. Write down the equations:
We have two equations based on the problem statement:
x+y=0.75(1)
x−y=0.25(2)
2. Add the two equations:
To eliminate y, we can add equations (1) and (2):
(x+y)+(x−y)=0.75+0.25
This simplifies to:
2x=1.00
3. Solve for x:
Dividing both sides by 2 gives:
x=0.50
4. Substitute x back to find y:
Now, substitute the value of x into equation (1):
0.50+y=0.75
Rearranging gives:
y=0.75−0.50=0.25
5. Summarize the values:
We have found:
x=0.50andy=0.25
6. Determine the coordination geometry:
- For x = 0.50, we check the range:
- The range for octahedral coordination is between 0.414 and 0.732. Since 0.50 falls within this range, the cation in AB is in an octahedral coordination.
- For y = 0.25, we check the range:
- The range for tetrahedral coordination is between 0.225 and 0.414. Since 0.25 falls within this range, the cation in CD is in a tetrahedral coordination.
7. Final answer:
Therefore, the cations in AB and CD are respectively in octahedral and tetrahedral coordination.
We have two equations based on the problem statement:
x+y=0.75(1)
x−y=0.25(2)
To eliminate y, we can add equations (1) and (2):
(x+y)+(x−y)=0.75+0.25
This simplifies to:
2x=1.00
Dividing both sides by 2 gives:
x=0.50
Now, substitute the value of x into equation (1):
0.50+y=0.75
Rearranging gives:
y=0.75−0.50=0.25
We have found:
x=0.50andy=0.25
- For x = 0.50, we check the range:
- The range for octahedral coordination is between 0.414 and 0.732. Since 0.50 falls within this range, the cation in AB is in an octahedral coordination.
- For y = 0.25, we check the range:
- The range for tetrahedral coordination is between 0.225 and 0.414. Since 0.25 falls within this range, the cation in CD is in a tetrahedral coordination.
Therefore, the cations in AB and CD are respectively in octahedral and tetrahedral coordination.
Topper's Solved these Questions
- THE SOLID STATE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THE SOLID STATE EXERCISE - ASSIGNMENT SECTION-C (OBJECTIVE)
17 Videos
- THE SOLID STATE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THE SOLID STATE EXERCISE - ASSIGNMENT SECTION-D (LINKED COMPREHENSION)
9 Videos
- THE SOLID STATE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THE SOLID STATE EXERCISE - ASSIGNMENT SECTION-A (OBJECTIVE)
50 Videos
- THE S-BLOCK ELEMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THE S-BLOCK ELEMENTSEXERCISE - Assignment (Section-J)
10 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - ASSIGNMENT (Section -D) Assertion-Reason Type Questions
15 Videos
Similar Questions
The equations of sides AB, BC and AC of ΔABC are respectively y=x, y=0 and 4x+3y=12, then find :
(i) length of perpendicular from B to AC
(ii)∠BAC.
View SolutionIF a=x2−2x+4x2+2x+4 and equation of lines AB and CD be 3y=xandy=3x respectively, then for all real x, point P(a,a2) (A) lies in the acute angle between lines AB and CD (B) lies in the obtuse angle between lines AB and CD (C) cannot be in the acute angle between lines AB and CD (D) cannot lie in the obtuse angle between lines AB and CD
View Solution
Knowledge Check
If the two lines of regression are 2x−y−4=0 and 9x−2y−38=0, then the means of x and y variates respectively are
A8, 6B6, 8C7 , 10D5, 6
The drawn alongiside (not drawn to scale) shows two stragit lines AB and CD. If the equation of line AB is: x−√3y+5=0 and the equation of line CD is : x−y=2, write down the inclinations of lines AB and CD, also find the angle θ i.e., angle CPB.
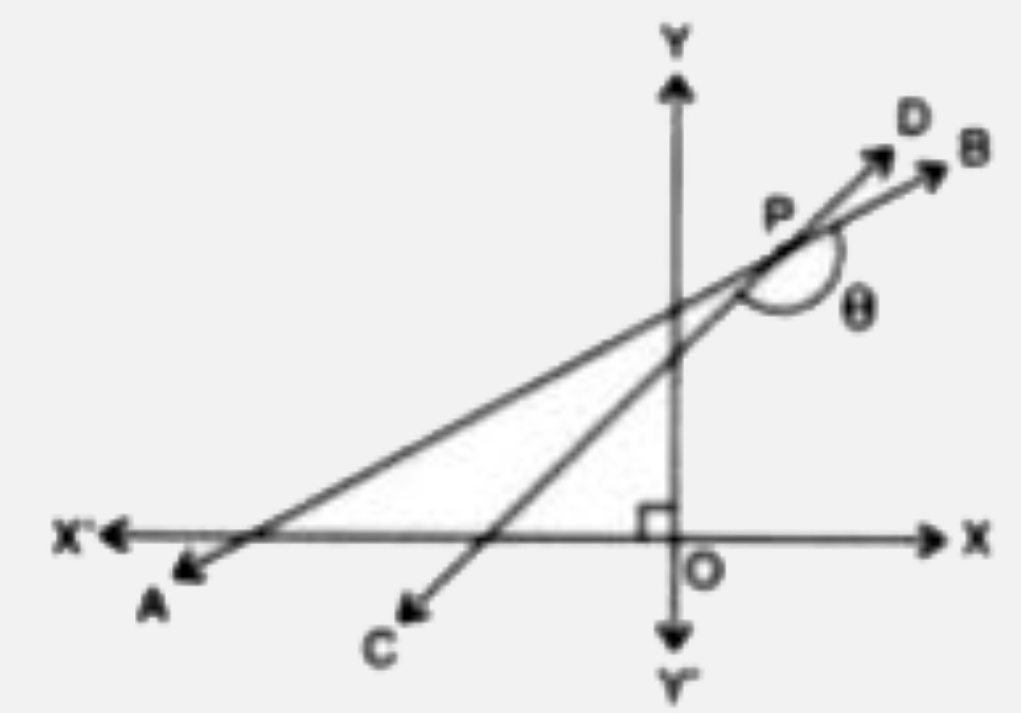
View SolutionThe sides AB and AD of a parallelogram ABCD are 2x−y+1=0andx+3y−10=0 respectively and C is the point (−1,−2). Find the equation of the diagonals AC.
View SolutionPoints A and B have co-ordinates (3, 5) and (x, y) respectively. The mid-point of AB is (2, 3). Find the values of x and y.
View SolutionLet ABC be a triangle with equations of the sides AB,BCandCA respectively x−2=0,y−5=0and5x+2y−10=0. Then the orthocentre of the triangle lies on the line
View Solution(a) the figure drawn alongside shows two straight lines AB and CD . if the equation of the line AB is x−√3y+5=0 and the equation of the line CD is x−y=2. write down the inclination of lines AB and CD; also find the angle θ i.e angle CPB
(b) if cosecθ.cos(θ+54∘)=1.find the value of θ so that θand(θ+54∘) are acute angles.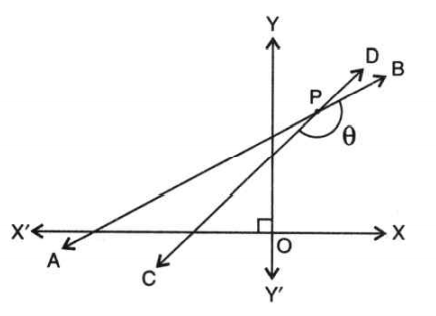
View SolutionThe equations of the sides AB and CA of a ΔABC are x+2y=0 and x−y=3 respectively. Given a fixed point P(2, 3).
Q. If P be orthocentre of ΔABC then equation of side BC is :
View SolutionIn a triangle ABC , if the equation of sides AB,BC and CA are 2x−y+4=0,x−2y−1=0andx+3y−3=0 respectively ,
The equation of external bisector of angle B is
View Solution
