On Ellingham diagrams if two graphs intersect each other, what does the point of intersection indicate ?
To answer the question regarding the significance of the intersection point of two graphs on an Ellingham diagram, we can break down the solution into the following steps:
1. Understanding the Ellingham Diagram:
- The Ellingham diagram is a plot that shows the relationship between the Gibbs free energy change (ΔG) of a reaction and temperature (T). It is used to predict the feasibility of reactions, particularly in metallurgy.
2. Identifying the Graphs:
- In the context of the question, we have two different reactions represented by their respective graphs on the Ellingham diagram.
3. Point of Intersection:
- The point where the two graphs intersect indicates that at that specific temperature, the Gibbs free energy change (ΔG) for both reactions is equal. This means that the reactions have the same thermodynamic favorability at that temperature.
4. Implications of the Intersection:
- At temperatures below the intersection point, one reaction is more favorable (has a more negative ΔG) than the other.
- At temperatures above the intersection point, the other reaction becomes more favorable.
- This implies that at temperatures greater than the intersection point, the reaction with the more negative ΔG can drive the other reaction, making it spontaneous.
5. Conclusion:
- The intersection point on the Ellingham diagram indicates a temperature at which two reactions can coexist, and the reaction with the lower Gibbs free energy can make the other reaction spontaneous.
- The Ellingham diagram is a plot that shows the relationship between the Gibbs free energy change (ΔG) of a reaction and temperature (T). It is used to predict the feasibility of reactions, particularly in metallurgy.
- In the context of the question, we have two different reactions represented by their respective graphs on the Ellingham diagram.
- The point where the two graphs intersect indicates that at that specific temperature, the Gibbs free energy change (ΔG) for both reactions is equal. This means that the reactions have the same thermodynamic favorability at that temperature.
- At temperatures below the intersection point, one reaction is more favorable (has a more negative ΔG) than the other.
- At temperatures above the intersection point, the other reaction becomes more favorable.
- This implies that at temperatures greater than the intersection point, the reaction with the more negative ΔG can drive the other reaction, making it spontaneous.
- The intersection point on the Ellingham diagram indicates a temperature at which two reactions can coexist, and the reaction with the lower Gibbs free energy can make the other reaction spontaneous.
Topper's Solved these Questions
- GENERAL PRINCIPLES AND PROCESSES OF ISOLATION OF ELEMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GENERAL PRINCIPLES AND PROCESSES OF ISOLATION OF ELEMENTSEXERCISE - Aakash Challengers Questions
8 Videos
- GENERAL PRINCIPLES AND PROCESSES OF ISOLATION OF ELEMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GENERAL PRINCIPLES AND PROCESSES OF ISOLATION OF ELEMENTSEXERCISE - Assignment (Section-D) Assertion-Reason Type Question
15 Videos
- HALOALKANES AND HALOARENES BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - HALOALKANES AND HALOARENES EXERCISE - ASSIGNMENT SECTION -D
15 Videos
Similar Questions
Can two isothermal curves intersect each other?
View SolutionMagnetic lines of force may intersect each other.
View SolutionSTATEMENT -1 : No two electric field line can intersect each other.
and
STATEMENT-2 : At point of intersection electric fieldmust be zero.
View SolutionTwo circles touching both the axes intersect at (3,-2) then the coordinates of their other point of intersection is
View SolutionProve that the line of centres of two intersecting circles subtends equal angles at the two points of intersection
View SolutionIn figure BD and CE intersect each other at the point P. IsΔPBC~ΔPDE? Why?

View SolutionIn the following diagram, lines l, m and n are parallel to each other. Two transversals p and q intersect the parallel lines at points A, B, C and P, Q, R as shown.
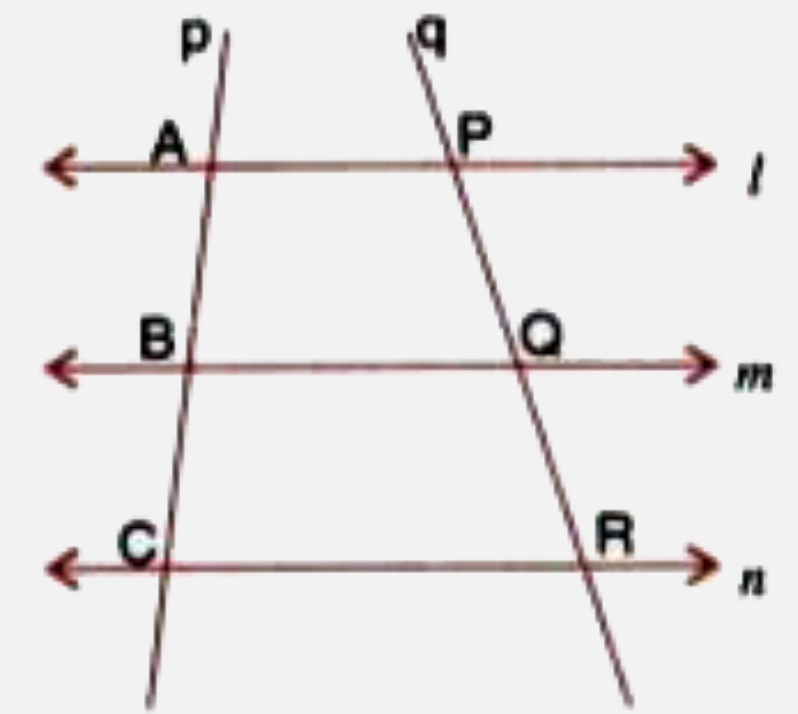
Prove that : ABBC=PQQR
Join A and R. Let AR meets BQ at point D.
View Solution(A) : No two electric lines of force can intersect each other
(R ): Tangent at any point of electric line of force gives the direction of electric field.
View SolutionIn some cases, Ellingham diagrams (graphs) show a bend. What do you refer from it ?
View SolutionIn some cases, Ellingham diagrams (graphs) show a bend. What do you refer from it ?
View Solution
