Two circles touching both the axes intersect at (3,-2) then the coordinates of their other point of intersection is
(2,3)
(2,-3)
(-2,3)
(-2,-3)
The correct Answer is:B
To solve the problem of finding the coordinates of the other point of intersection of two circles that touch both axes and intersect at the point (3, -2), we can follow these steps:
Step 1: Understand the Problem
We have two circles that touch both the x-axis and y-axis and intersect at the point (3, -2). We need to find the coordinates of their other point of intersection.
Hint: Visualize the circles and their properties. Since they touch both axes, their centers will be located along the line y = -x.
Step 2: Identify the Line of Centers
The centers of the circles must lie on the line y = -x, which can also be expressed as x + y = 0.
Hint: This line represents the symmetry of the circles with respect to the origin.
Step 3: Use the Reflection Property
To find the other point of intersection, we can reflect the point (3, -2) across the line y = -x. The reflection of a point (x1, y1) across the line ax + by + c = 0 can be calculated using the formula:
- h=x1−2a(ax1+by1+c)a2+b2
- k=y1−2b(ax1+by1+c)a2+b2
For our line x + y = 0, we have:
- a=1,b=1,c=0
- The point (x1, y1) = (3, -2)
Hint: Substitute the values into the reflection formula.
Step 4: Calculate the Reflection
1. Calculate ax1+by1+c:
- 1(3)+1(−2)+0=3−2+0=1
2. Substitute into the formulas:
- h=3−2(1)(1)12+12=3−22=3−1=2
- k=−2−2(1)(1)12+12=−2−22=−2−1=−3
Hint: Ensure you perform the arithmetic correctly.
Step 5: Conclusion
The coordinates of the other point of intersection of the two circles are (2, -3).
Final Answer: (2, -3)
We have two circles that touch both the x-axis and y-axis and intersect at the point (3, -2). We need to find the coordinates of their other point of intersection.
The centers of the circles must lie on the line y = -x, which can also be expressed as x + y = 0.
To find the other point of intersection, we can reflect the point (3, -2) across the line y = -x. The reflection of a point (x1, y1) across the line ax + by + c = 0 can be calculated using the formula:
- h=x1−2a(ax1+by1+c)a2+b2
- k=y1−2b(ax1+by1+c)a2+b2
- a=1,b=1,c=0
- The point (x1, y1) = (3, -2)
1. Calculate ax1+by1+c:
- 1(3)+1(−2)+0=3−2+0=1
- h=3−2(1)(1)12+12=3−22=3−1=2
- k=−2−2(1)(1)12+12=−2−22=−2−1=−3
The coordinates of the other point of intersection of the two circles are (2, -3).
Similar Questions
Circle touching both the axes and radius 5 is
View SolutionIf two circles touching both the axes intersect at two points P and Q where P=(3,1) then PQ=
View SolutionIf two circles touching both the axes are passing through (2,3) then length of their common chord is
View SolutionIf two adjacent vertices of a parallelogram are (3, 2) and (-1, 0) and the diagonals intersect at (2, -5), then find the coordinates of the other two vertices.
View SolutionA circle touches both the coordinate axes and the line x−y=√2a,a>0, the coordinates of the centre of the circle cannot be
View SolutionThe straight line x-2y+1=0 intersects the circle x2+y2=25 in points P and Q the coordinates of the point of intersection of tangents drawn at P and Q to the circle is
View Solution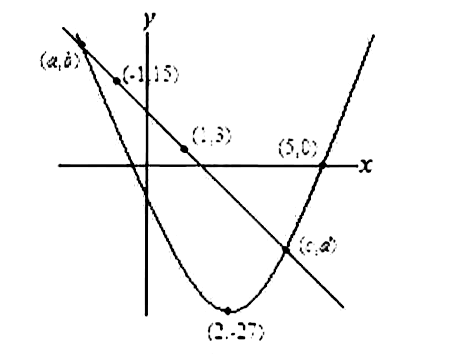
The xy-plane above shows the two points of intersection of the graphs of a linear function and a quadratic function. The leftmost point of intersection has coordinates (a,b) and the rightmost point of intersection has coordinates (c,d) . If the vertex of the graph of the quadratic function is at (2, -27) , what is the value of b−d ?
View SolutionCentre of circles touching both axes and passing through (2,-3)
View SolutionOn Ellingham diagrams if two graphs intersect each other, what does the point of intersection indicate ?
View SolutionOn Ellingham diagrams if two graphs intersect each other, what does the point of intersection indicate ?
View Solution
