How it is possible to find the value of ΔU and not the value of U?
ΔU can be calculated in term of 'W' and 'q' by first law but internal energy (U) cannot be calculated practically by adding for each molecule.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - SECTION-A45videos
THERMODYNAMICS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - SECTION-B20videos
THERMODYNAMICS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - ASSIGNMENT (Section -D) Assertion-Reason Type Questions15videos
THERMODYNAMICS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THE SOLID STATE EXERCISE - Assignment (SECTION - D) (ASSERTION-REASON TYPE QUESTION)20videos
THE SOLID STATE
Similar Questions
3. Find the value of x and y in the given triangle
View SolutionA system absorbs 800 J of heat and system works equivalent to 900 J by expanding. The value of ΔU for the system is
View SolutionA sample of an ideal gas initially having internal energy U1 is allowed to expand adiabatically performing work W. Heat Q is then supplied to it, keeping the volume constant at its new value, until the pressure raised to its original value. The internal energy is then U3 (see figure). find the increase in internal energy (U3−U1)?
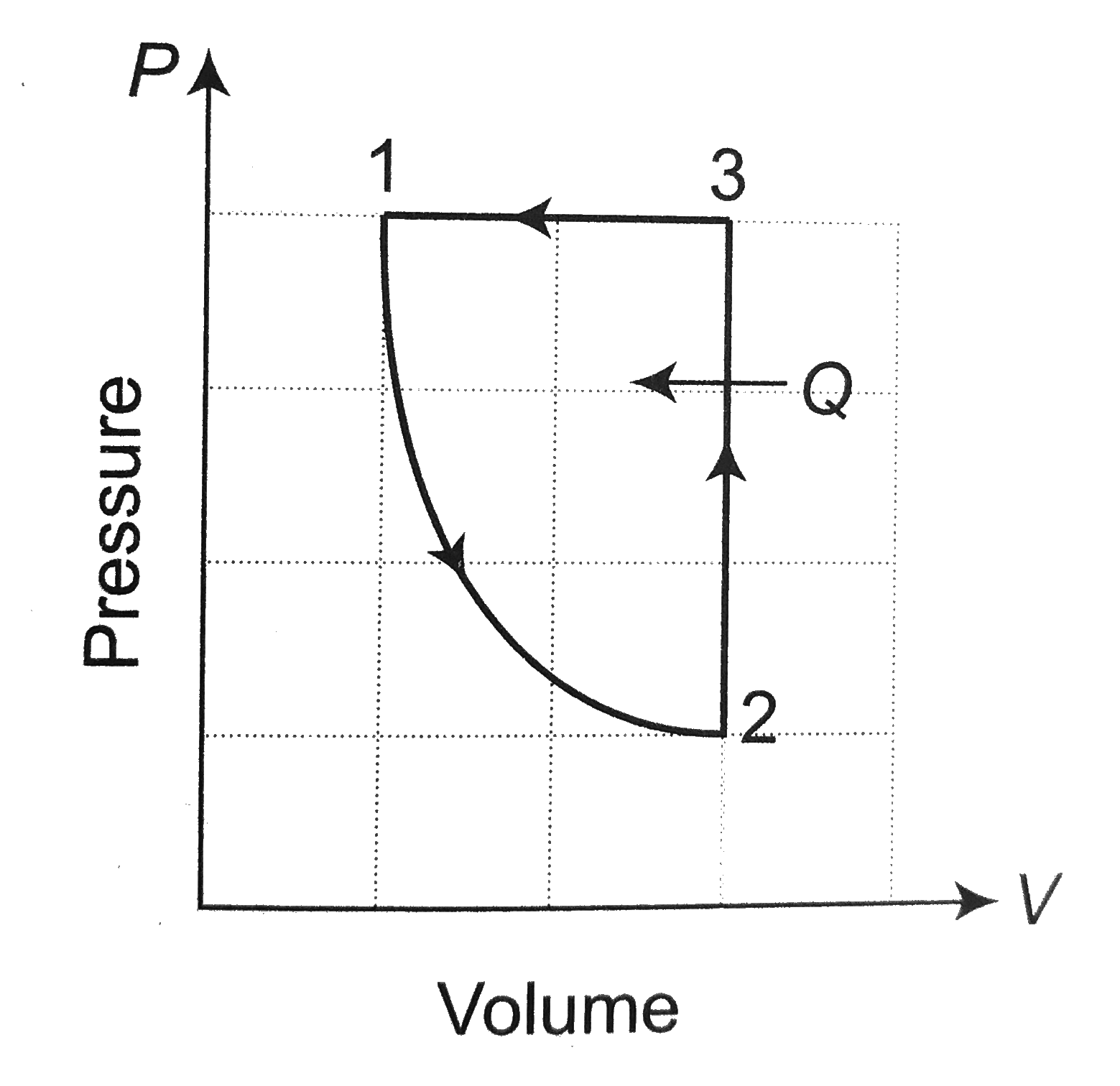 View Solution
View SolutionLet A,B,C, be three angles such that A=π4 and tanBtanC=p. Find all possible values of p such that A,B,C are the angles of a triangle.
View SolutionLet A,B,C, be three angles such that A=π4 and tanBtanC=p. Find all possible values of p such that A,B,C are the angles of a triangle.
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle. Find the value of ∠BDC and ∠BEC.
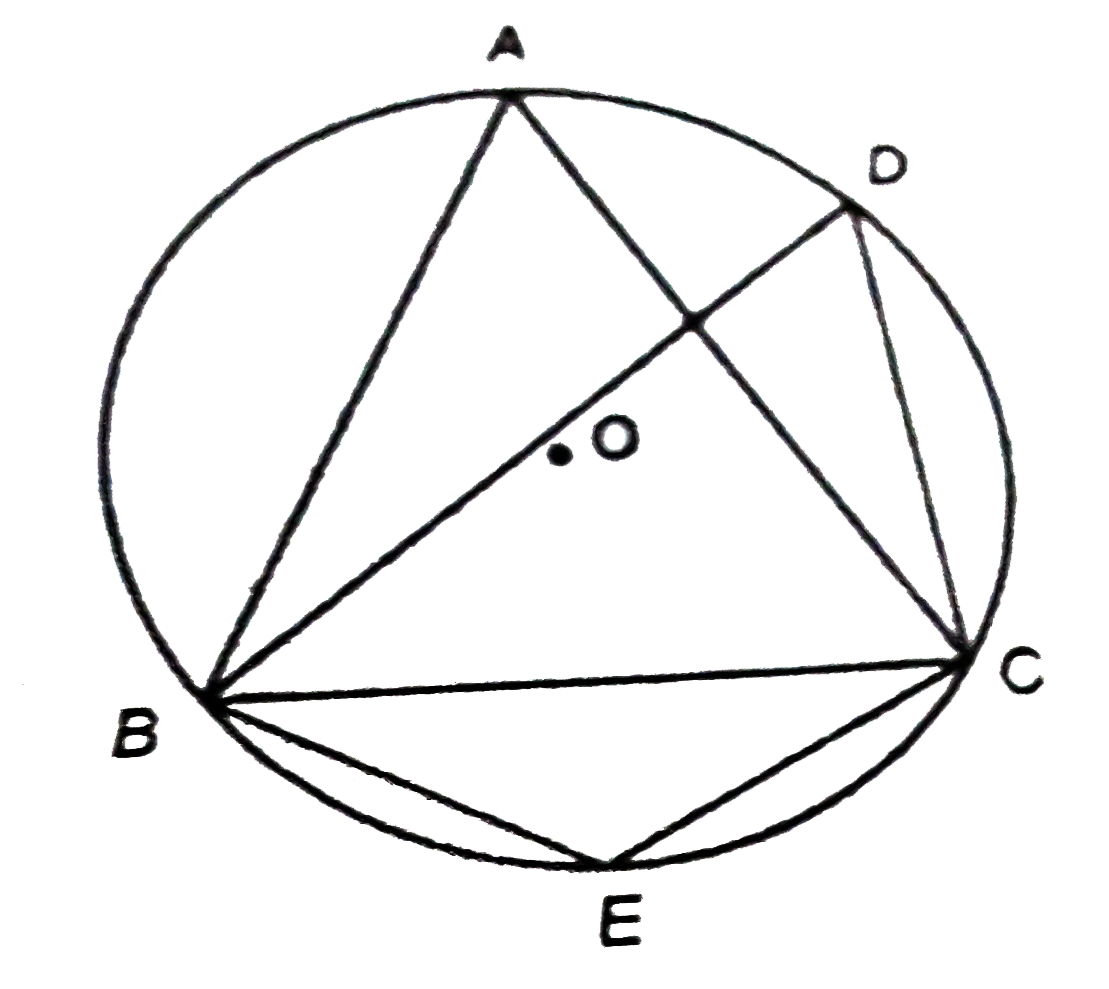 View Solution
View SolutionIn the given figure, three coplanar lines intersect at a point O, forming angles as shown in the figure. Find the value of x,y,z and u.
View SolutionThe relation between U, p and V for an ideal gas in an adiabatic process is given by relation U=a+bpV. Find the value of adiabatic exponent (γ) of this gas.
View SolutionIf n(U)=50, n(A)=24, and n(B)= 30 where U is the universal set, then find
(i) The greatest value of n(A∪B)
(ii) The least value of n(A∩B)View SolutionIf n(U)=1200, n(A)=900 and n(B)=700 where U is the universal set then find:
(i) The greatest value of n(A∪B)
(ii) The least value of n(A∩B).View Solution

