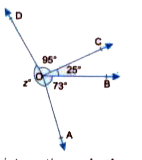
In the given figure, three coplanar lines intersect at a point O, forming angles as shown in the figure. Find the value of x,y,z and u.
To solve the problem step by step, we will analyze the angles formed by the intersection of the three coplanar lines at point O.
Step 1: Identify the angles
From the problem, we have the following angles:
- Angle AOF = U
- Angle BOD = 90°
- Angle DOF = 50°
- Angle Y = 50° (as given)
- Angle Z = 90° (as given)
- Angle X = ?
Step 2: Use the straight line property
Since angles BOD, DOF, and AOF are on a straight line, we can use the property that the sum of angles on a straight line is 180°.
So, we can write the equation:
Angle BOD+Angle DOF+Angle AOF=180°
Step 3: Substitute the known values
Substituting the known values into the equation:
90°+50°+U=180°
Step 4: Simplify the equation
Now, simplify the left side:
140°+U=180°
Step 5: Solve for U
To find U, subtract 140° from both sides:
U=180°−140°
U=40°
Step 6: Find the value of X
Since angle X and angle U are vertically opposite angles, they are equal:
X=U=40°
Step 7: Find the value of Y and Z
From the problem statement:
- Angle Y is given as 50°.
- Angle Z is given as 90°.
Final Values
Thus, we have:
- U=40°
- X=40°
- Y=50°
- Z=90°
Summary of Results
- X=40°
- Y=50°
- Z=90°
- U=40°
---
From the problem, we have the following angles:
- Angle AOF = U
- Angle BOD = 90°
- Angle DOF = 50°
- Angle Y = 50° (as given)
- Angle Z = 90° (as given)
- Angle X = ?
Since angles BOD, DOF, and AOF are on a straight line, we can use the property that the sum of angles on a straight line is 180°.
Angle BOD+Angle DOF+Angle AOF=180°
Substituting the known values into the equation:
90°+50°+U=180°
Now, simplify the left side:
140°+U=180°
To find U, subtract 140° from both sides:
U=180°−140°
U=40°
Since angle X and angle U are vertically opposite angles, they are equal:
X=U=40°
From the problem statement:
- Angle Y is given as 50°.
- Angle Z is given as 90°.
Thus, we have:
- U=40°
- X=40°
- Y=50°
- Z=90°
- X=40°
- Y=50°
- Z=90°
- U=40°
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the given figure, find the value of z
 A167∘B157∘C147∘D137∘
A167∘B157∘C147∘D137∘
Inthegivenfigure,f∈dthevalueofx+y
View SolutionIn figure, lines l1and l2 intersect at O, forming angles as shown in the figure. If x=45∘ , find the values of y, z and u.
View SolutionIn Fig. 30, lines l1 and l2 intersect at O, forming angles as shown in the figure. If x=450, find the values of y,z and u.
View SolutionIn Figure, lines l1and L2 intersect at O , forming angles as shown in the figure. If a=350, find the values of b, c and d.
View SolutionIn Figure, three coplanar lines intersect in a common point, forming angles as shown Given ∠DOF=500 and ∠BOD=900; find the values of x, y, z and u.
View SolutionIn Fig.10, lines l1 and l2 interest at O, forming angles as shown in the figure. If a=35, find the value of b,c and d.
View SolutionIn the given figure, find x,y and z.
View Solution
