1 mole of an ideal gas is expanded from an initial pressure of 1 bar to final pressure of 0.1 bar at constant temperature of 273 K. Predict which of the following is not true?
ΔE = 0
ΔH = 0
PV is constant
ΔS←0
The correct Answer is:D
To solve the problem step by step, we will analyze the situation of the ideal gas expansion and apply the relevant thermodynamic principles.
Step 1: Understand the Given Information
We have:
- 1 mole of an ideal gas
- Initial pressure (P1) = 1 bar
- Final pressure (P2) = 0.1 bar
- Constant temperature (T) = 273 K
Step 2: Identify the Thermodynamic Process
Since the temperature is constant, this is an isothermal process. For an ideal gas undergoing an isothermal expansion, we can apply the ideal gas law and the first law of thermodynamics.
Step 3: Apply the First Law of Thermodynamics
The first law of thermodynamics states:
ΔU=Q−W
Where:
- ΔU = change in internal energy
- Q = heat added to the system
- W = work done by the system
For an ideal gas, the change in internal energy (ΔU) is given by:
ΔU=nCvΔT
Since the process is isothermal (ΔT=0), we have:
ΔU=0
Step 4: Determine the Work Done (W)
In an isothermal process for an ideal gas, the work done (W) can be calculated using:
W=nRTln(P1P2)
Substituting the values:
- n=1 mole
- R=0.08314L bar K−1mol−1
- T=273K
- P1=1bar
- P2=0.1bar
Calculating the work done:
W=1×0.08314×273×ln(10.1)
W=0.08314×273×ln(10)
W≈0.08314×273×2.3026≈62.36L bar(convert to Joules if needed)
Step 5: Analyze the Options
Now, we need to determine which statement is not true based on our findings:
1. ΔU=0 (True)
2. ΔH=0 (True, since ΔH=ΔU+Δ(PV) and Δ(PV)=0 in isothermal conditions)
3. Volume is constant (Not true, as the volume changes during expansion)
4. ΔS=0 (Not true, as entropy increases during expansion)
Conclusion
The statement that is not true is that the volume is constant. Therefore, the correct answer is that the statement regarding constant volume is incorrect.
We have:
- 1 mole of an ideal gas
- Initial pressure (P1) = 1 bar
- Final pressure (P2) = 0.1 bar
- Constant temperature (T) = 273 K
Since the temperature is constant, this is an isothermal process. For an ideal gas undergoing an isothermal expansion, we can apply the ideal gas law and the first law of thermodynamics.
The first law of thermodynamics states:
ΔU=Q−W
Where:
- ΔU = change in internal energy
- Q = heat added to the system
- W = work done by the system
ΔU=nCvΔT
Since the process is isothermal (ΔT=0), we have:
ΔU=0
In an isothermal process for an ideal gas, the work done (W) can be calculated using:
W=nRTln(P1P2)
Substituting the values:
- n=1 mole
- R=0.08314L bar K−1mol−1
- T=273K
- P1=1bar
- P2=0.1bar
W=1×0.08314×273×ln(10.1)
W=0.08314×273×ln(10)
W≈0.08314×273×2.3026≈62.36L bar(convert to Joules if needed)
Now, we need to determine which statement is not true based on our findings:
1. ΔU=0 (True)
2. ΔH=0 (True, since ΔH=ΔU+Δ(PV) and Δ(PV)=0 in isothermal conditions)
3. Volume is constant (Not true, as the volume changes during expansion)
4. ΔS=0 (Not true, as entropy increases during expansion)
The statement that is not true is that the volume is constant. Therefore, the correct answer is that the statement regarding constant volume is incorrect.
Topper's Solved these Questions
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - SECTION-C
13 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - SECTION-D
9 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - SECTION-A
45 Videos
- THE SOLID STATE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THE SOLID STATE EXERCISE - Assignment (SECTION - D) (ASSERTION-REASON TYPE QUESTION)
20 Videos
Similar Questions
Calculate q,w, and ΔU for the isothermal reversible expansion of one mole of an ideal gas from an initial pressure of 2.0 bar to a final pressure of 0.2 bar at a constant temperature of 273K.
View SolutionCalculate q,w,ΔU, and ΔH for this isothermal reversible expansion of 1mole of an ideal gas from an initial pressure of 1.0 bar to final pressure of 0.1bar at a constant pressure of 273K.
View SolutionThe pressure-volume of varies thermodynamic process is shown in graphs:
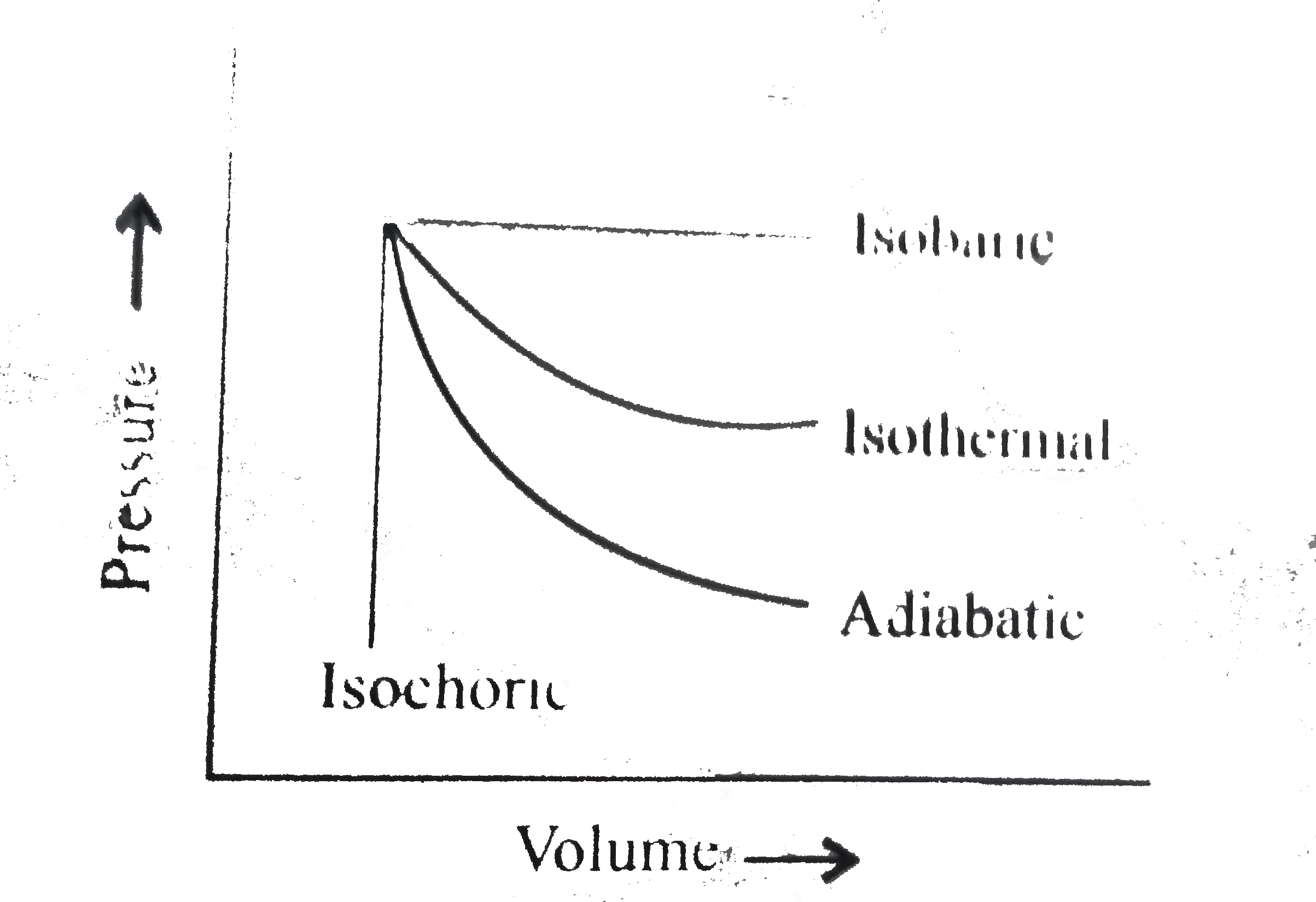
Work is the mole of transference of energy. It has been observed that reversible work done by the system is the maximum obtainable work.
wrev>wirr
The works of isothermal and adiabatic processes are different from each other.
wisothermal reversible=2.303nRTlog10(V2V1)
=2.303nRTlog10(P2P1)
wadiabatic reversible=CV(T1−T2)
The q value and work done in isothermal reversible expansion of one mole of an ideal gas from initial pressure of 1 bar to final pressure of 0.1 bar at constant temperature 273K are:
View SolutionOne mole of an ideal gas is expanded from a volume of 3L to 5L under a constant pressure of 1 atm. Calculate the work done by the gas.
View SolutionBy how much does the entropy of 3 mole of an ideal gas change in going from a pressure of 2 bar to a pressure of 1 bar without any change in Temperature . If the surrounding is at 1 bar and 300 K (Expansion is again of the cosntant extenal pressure of surrounding).
View SolutionCalculate the work done when 1 mol of an ideal gas is compressed reversibly from 1 bar to 4 bar at a constant temperature of 300 K
View Solution5 mole of an ideal gas expand isothermally and irreversibly from a pressure of 10 atm to 1 atm against a constant external
pressure of 2 atm. wirr at 300 K is :
View SolutionIf pressure is 1 bar, then the boiling temperature is called
View Solution2 mole of an ideal monoatomic gas undergoes a reversible process for which PV2=C. The gas is expanded from initial volume of 1 L to final volume of 3 L starting from initial temperature of 300 K. Find ΔH for the process :
View SolutionIn an isothermal process at 300 K, 1 mole of an ideal gas expands from a pressure 100 atm against an external pressure of 50 atm. Then total entropy change (Cal K−1) in the process is -
View Solution
